https://www.topcoder.com/community/competitive-programming/tutorials/geometry-concepts-basic-concepts/



https://www.mathsisfun.com/algebra/vectors.html



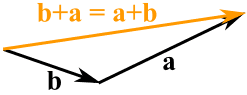

https://www.topcoder.com/community/competitive-programming/tutorials/geometry-concepts-basic-concepts/
X. Dot Product
https://www.mathsisfun.com/algebra/vectors-dot-product.html

https://www.mathsisfun.com/algebra/vectors-cross-product.html
And it all happens in 3 dimensions!
Cartesian coordinate system
笛卡儿坐标系(Cartesian coordinate system),也称直角坐标系,是一种正交坐标系。参阅图1,二维的直角坐标系是由两条相互垂直、0点重合的数轴构成的。在平面内,任何一点的坐标是根据数轴上对应的点的坐标设定的。
Polar coordinate system
极坐标系是一个二维坐标系统。该坐标系统中任意位置可由一个夹角和一段相对原点—极点的距离来表示。
极坐标系也有两个坐标轴: (半径坐标)和
(半径坐标)和 (角坐标、极角或方位角,有时也表示为
(角坐标、极角或方位角,有时也表示为 或
或 )。
)。 坐标表示与极点的距离,
坐标表示与极点的距离, 坐标表示按逆时针方向坐标距离0°射线(有时也称作极轴)的角度,极轴就是在平面直角坐标系中的x轴正方向
坐标表示按逆时针方向坐标距离0°射线(有时也称作极轴)的角度,极轴就是在平面直角坐标系中的x轴正方向
Polar angle

Vectors
Vectors are the basis of a lot of methods for solving geometry problems. Formally, a vector is defined by a direction and a magnitude. In the case of two-dimension geometry, a vector can be represented as pair of numbers, x and y, which gives both a direction and a magnitude. For example, the line segment from (1,3) to (5,1) can be represented by the vector (4,-2). It’s important to understand, however, that the vector defines only the direction and magnitude of the segment in this case, and does not define the starting or ending locations of the vector.
Vectors are the basis of a lot of methods for solving geometry problems. Formally, a vector is defined by a direction and a magnitude. In the case of two-dimension geometry, a vector can be represented as pair of numbers, x and y, which gives both a direction and a magnitude. For example, the line segment from (1,3) to (5,1) can be represented by the vector (4,-2). It’s important to understand, however, that the vector defines only the direction and magnitude of the segment in this case, and does not define the starting or ending locations of the vector.
Vector Addition
There are a number of mathematical operations that can be performed on vectors. The simplest of these is addition: you can add two vectors together and the result is a new vector. If you have two vectors (x1, y1) and (x2, y2), then the sum of the two vectors is simply (x1+x2, y1+y2). The image below shows the sum of four vectors. Note that it doesn’t matter which order you add them up in – just like regular addition. Throughout these articles, we will use plus and minus signs to denote vector addition and subtraction, where each is simply the piecewise addition or subtraction of the components of the vector.
There are a number of mathematical operations that can be performed on vectors. The simplest of these is addition: you can add two vectors together and the result is a new vector. If you have two vectors (x1, y1) and (x2, y2), then the sum of the two vectors is simply (x1+x2, y1+y2). The image below shows the sum of four vectors. Note that it doesn’t matter which order you add them up in – just like regular addition. Throughout these articles, we will use plus and minus signs to denote vector addition and subtraction, where each is simply the piecewise addition or subtraction of the components of the vector.
Dot Product
The addition of vectors is relatively intuitive; a couple of less obvious vector operations are dot and cross products. The dot product of two vectors is simply the sum of the products of the corresponding elements. For example, the dot product of (x1, y1) and (x2, y2) is x1*x2 + y1*y2. Note that this is not a vector, but is simply a single number (called a scalar). The reason this is useful is that the dot product, A ⋅ B = |A||B|Cos(θ), where θ is the angle between the A and B. |A| is called the norm of the vector, and in a 2-D geometry problem is simply the length of the vector, sqrt(x2+y2). Therefore, we can calculate Cos(θ) = (A ⋅ B)/(|A||B|). By using the acos function, we can then find θ. It is useful to recall that Cos(90) = 0 and Cos(0) = 1, as this tells you that a dot product of 0 indicates two perpendicular lines, and that the dot product is greatest when the lines are parallel. A final note about dot products is that they are not limited to 2-D geometry. We can take dot products of vectors with any number of elements, and the above equality still holds.
The addition of vectors is relatively intuitive; a couple of less obvious vector operations are dot and cross products. The dot product of two vectors is simply the sum of the products of the corresponding elements. For example, the dot product of (x1, y1) and (x2, y2) is x1*x2 + y1*y2. Note that this is not a vector, but is simply a single number (called a scalar). The reason this is useful is that the dot product, A ⋅ B = |A||B|Cos(θ), where θ is the angle between the A and B. |A| is called the norm of the vector, and in a 2-D geometry problem is simply the length of the vector, sqrt(x2+y2). Therefore, we can calculate Cos(θ) = (A ⋅ B)/(|A||B|). By using the acos function, we can then find θ. It is useful to recall that Cos(90) = 0 and Cos(0) = 1, as this tells you that a dot product of 0 indicates two perpendicular lines, and that the dot product is greatest when the lines are parallel. A final note about dot products is that they are not limited to 2-D geometry. We can take dot products of vectors with any number of elements, and the above equality still holds.
Cross Product
An even more useful operation is the cross product. The cross product of two 2-D vectors is x1*y2 - y1*x2 Technically, the cross product is actually a vector, and has the magnitude given above, and is directed in the +z direction. Since we’re only working with 2-D geometry for now, we’ll ignore this fact, and use it like a scalar. Similar to the dot product, A x B = |A||B|Sin(θ). However, θ has a slightly different meaning in this case: |θ| is the angle between the two vectors, but θ is negative or positive based on the right-hand rule. In 2-D geometry this means that if A is less than 180 degrees clockwise from B, the value is positive. Another useful fact related to the cross product is that the absolute value of |A||B|Sin(θ) is equal to the area of the parallelogram with two of its sides formed by A and B. Furthermore, the triangle formed by A, B and the red line in the diagram has half of the area of the parallelogram, so we can calculate its area from the cross product also.
An even more useful operation is the cross product. The cross product of two 2-D vectors is x1*y2 - y1*x2 Technically, the cross product is actually a vector, and has the magnitude given above, and is directed in the +z direction. Since we’re only working with 2-D geometry for now, we’ll ignore this fact, and use it like a scalar. Similar to the dot product, A x B = |A||B|Sin(θ). However, θ has a slightly different meaning in this case: |θ| is the angle between the two vectors, but θ is negative or positive based on the right-hand rule. In 2-D geometry this means that if A is less than 180 degrees clockwise from B, the value is positive. Another useful fact related to the cross product is that the absolute value of |A||B|Sin(θ) is equal to the area of the parallelogram with two of its sides formed by A and B. Furthermore, the triangle formed by A, B and the red line in the diagram has half of the area of the parallelogram, so we can calculate its area from the cross product also.
https://www.mathsisfun.com/algebra/vectors.html
This is a vector:

A vector has magnitude (size) and direction:

The length of the line shows its magnitude and the arrowhead points in the direction.
We can add two vectors by joining them head-to-tail:

And it doesn't matter which order we add them, we get the same result:
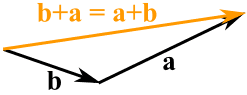
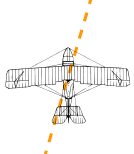
Example: A plane is flying along, pointing North, but there is a wind coming from the North-West.

The two vectors (the velocity caused by the propeller, and the velocity of the wind) result in a slightly slower ground speed heading a little East of North.
If you watched the plane from the ground it would seem to be slipping sideways a little.

Have you ever seen that happen? Maybe you have seen birds struggling against a strong wind that seem to fly sideways. Vectors help explain that
https://www.topcoder.com/community/competitive-programming/tutorials/geometry-concepts-basic-concepts/
Vectors
Vectors are the basis of a lot of methods for solving geometry problems. Formally, a vector is defined by a direction and a magnitude. In the case of two-dimension geometry, a vector can be represented as pair of numbers, x and y, which gives both a direction and a magnitude. For example, the line segment from (1,3) to (5,1) can be represented by the vector (4,-2). It’s important to understand, however, that the vector defines only the direction and magnitude of the segment in this case, and does not define the starting or ending locations of the vector.
Vectors are the basis of a lot of methods for solving geometry problems. Formally, a vector is defined by a direction and a magnitude. In the case of two-dimension geometry, a vector can be represented as pair of numbers, x and y, which gives both a direction and a magnitude. For example, the line segment from (1,3) to (5,1) can be represented by the vector (4,-2). It’s important to understand, however, that the vector defines only the direction and magnitude of the segment in this case, and does not define the starting or ending locations of the vector.
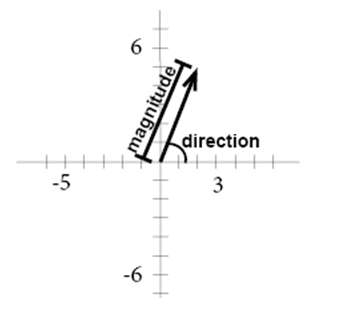
Vectors are used to represent a quantity that has both a magnitude and a direction. The vector is normally visualized in a graph. A vector between A and B is written as
The vectors standard position has its starting point in origin.

The component form of a vector is the ordered pair that describes the changes in the x- and y-values. In the graph above x1=0, y1=0 and x2=2, y2=5. The ordered pair that describes the changes is (x2- x1, y2- y1), in our example (2-0, 5-0) or (2,5).
Two vectors are equal if they have the same magnitude and direction. They are parallel if they have the same or opposite direction.
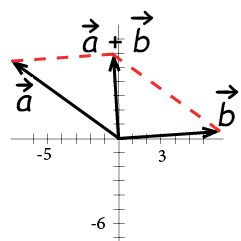
We can combine vectors by adding them, the sum of two vectors is called the resultant.

In order to add two vectors, we add the corresponding components.
Add the two following vectors:
We add the corresponding components
https://www.mathsisfun.com/algebra/vectors-dot-product.html
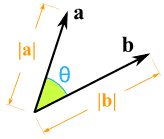
Here are two vectors:

They can be multiplied using the "Dot Product" (also see Cross Product).
Calculating
The Dot Product gives a number as an answer (a "scalar", not a vector).
The Dot Product is written using a central dot:
a · b
This means the Dot Product of a and b
This means the Dot Product of a and b
We can calculate the Dot Product of two vectors this way:

a · b = |a| × |b| × cos(θ)
Where:
|a| is the magnitude (length) of vector a
|b| is the magnitude (length) of vector bθ is the angle between a and b
|a| is the magnitude (length) of vector a
|b| is the magnitude (length) of vector bθ is the angle between a and b
So we multiply the length of a times the length of b, then multiply by the cosine of the angle between a and b
OR we can calculate it this way:

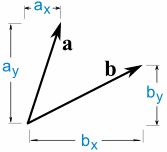
a · b = ax × bx + ay × by
So we multiply the x's, multiply the y's, then add.
Both methods work!
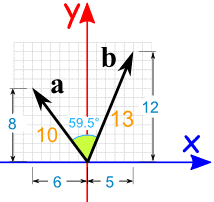
Example: Calculate the dot product of vectors a and b:

a · b = |a| × |b| × cos(θ)
a · b = 10 × 13 × cos(59.5°)
a · b = 10 × 13 × 0.5075...
a · b = 65.98... = 66 (rounded)
or we can calculate it this way:
a · b = ax × bx + ay × by
a · b = -6 × 5 + 8 × 12
a · b = -30 + 96
a · b = 66
Both methods came up with the same result (after rounding)
Also note that we used minus 6 for ax (it is heading in the negative x-direction)
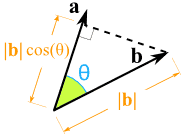
Why cos(θ) ?
OK, to multiply two vectors it makes sense to multiply their lengths together but only when they point in the same direction.
So we make one "point in the same direction" as the other by multiplying by cos(θ):
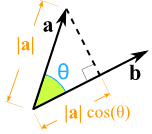 |  | |
| We take the component of a that lies alongside b | Like shining a light to see where the shadow lies |
THEN we multiply !
| It works exactly the same if we "projected" b alongside a then multiplied: Because it doesn't matter which order we do the multiplication:
|a| × |b| × cos(θ) = |a| × cos(θ) × |b|
|  |
Right Angles
When two vectors are at right angles to each other the dot product is zero.
Example: Sam has measured the end-points of two poles, and wants to know the angle between them:

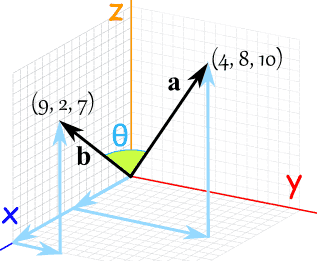
We have 3 dimensions, so don't forget the z-components:
a · b = ax × bx + ay × by + az × bz
a · b = 9 × 4 + 2 × 8 + 7 × 10
a · b = 36 + 16 + 70
a · b = 122
Now for the other formula:
a · b = |a| × |b| × cos(θ)
But what is |a| ? It is the magnitude, or length, of the vector a. We can use Pythagoras:
- |a| = √(42 + 82 + 102)
- |a| = √(16 + 64 + 100)
- |a| = √180
Likewise for |b|:
- |b| = √(92 + 22 + 72)
- |b| = √(81 + 4 + 49)
- |b| = √134
And we know from the calculation above that a · b = 122, so:
a · b = |a| × |b| × cos(θ)
122 = √180 × √134 × cos(θ)
cos(θ) = 122 / (√180 × √134)
cos(θ) = 0.7855...
θ = cos-1(0.7855...) = 38.2...°
The Dot Product gives a scalar (ordinary number) answer, and is sometimes called the scalar product.
But there is also the Cross Product which gives a vector as an answer, and is sometimes called the vector product.
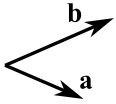
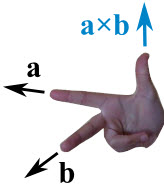
Two vectors can be multiplied using the "Cross Product" (also see Dot Product)

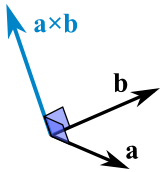
The Cross Product a × b of two vectors is another vector that is at right angles to both:

And it all happens in 3 dimensions!
Calculating
We can calculate the Cross Product this way:

a × b = |a| |b| sin(θ) n
- |a| is the magnitude (length) of vector a
- |b| is the magnitude (length) of vector b
- θ is the angle between a and b
- n is the unit vector at right angles to both a and b
So the length is: the length of a times the length of b times the sine of the angle between a and b,
Then we multiply by the vector n to make sure it heads in the right direction (at right angles to both a and b).
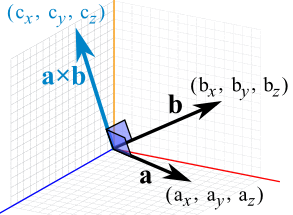
OR we can calculate it this way:

When a and b start at the origin point (0,0,0), the Cross Product will end at:
- cx = aybz − azby
- cy = azbx − axbz
- cz = axby − aybx

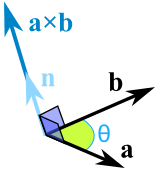
Which Direction?
The cross product could point in the completely opposite direction and still be at right angles to the two other vectors, so we have the:
"Right Hand Rule"
With your right-hand, point your index finger along vector a, and point your middle finger along vector b: the cross product goes in the direction of your thumb.
Cartesian coordinate system
笛卡儿坐标系(Cartesian coordinate system),也称直角坐标系,是一种正交坐标系。参阅图1,二维的直角坐标系是由两条相互垂直、0点重合的数轴构成的。在平面内,任何一点的坐标是根据数轴上对应的点的坐标设定的。
Polar coordinate system
极坐标系是一个二维坐标系统。该坐标系统中任意位置可由一个夹角和一段相对原点—极点的距离来表示。
极坐标系也有两个坐标轴:
 (半径坐标)和
(半径坐标)和 (角坐标、极角或方位角,有时也表示为
(角坐标、极角或方位角,有时也表示为 或
或 )。
)。 坐标表示与极点的距离,
坐标表示与极点的距离, 坐标表示按逆时针方向坐标距离0°射线(有时也称作极轴)的角度,极轴就是在平面直角坐标系中的x轴正方向
坐标表示按逆时针方向坐标距离0°射线(有时也称作极轴)的角度,极轴就是在平面直角坐标系中的x轴正方向Polar angle