Isotonic Regression | Algorithms Notes
Given a sequence A of n integers, design an algorithm to find an non-decreasing sequence B of n integers, such that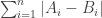
is minimized.
http://stackoverflow.com/questions/28149331/given-a-sequence-a1-a2-an-find-an-array-b1-b2-bn-s
Solution:
This problem can be solved by minimum cost flow. Here we use dynamic programming.
Let F(k, z) be the optimal objective value for the first k elements with B[k] = z. Then, we have a recurrence relation: F(k, z) = min F(k-1, x) + |z – A[k]|. Thus, the problem becomes how to efficiently find the z minimizing F(k, z) for all fixed k. It can be showed that F(k, z) is a piecewise linear convex function in z and the minimizing value must be in A. Thus, the dynamic programming can be speed up by using slope optimization and find the solution in O(n lg n) time.
令 F(k, z) 為前 k 個元素且 B[k] = z 時的最佳解之值。當給定 k ，我們可得一遞回關係式：F(k, z) = min F(k-1, x) + |z – A[k]|。因此問題就變成如何快速的找出最小化 F(k, z) 的 z 值。我們可以證明 F(k, z) 對於 z 是一個 piecewise linear convex 函數 ，而且可以最小化 F 的 z 值必定在 A 中。因此使用動態規劃加上斜率最佳化可以在O(n lg n)時間內找到答案。
http://stackoverflow.com/questions/10460861/finding-an-increasing-sequence-a-which-minimizes-sigmaabsaici
Read full article from Isotonic Regression | Algorithms Notes
Given a sequence A of n integers, design an algorithm to find an non-decreasing sequence B of n integers, such that
is minimized.http://stackoverflow.com/questions/28149331/given-a-sequence-a1-a2-an-find-an-array-b1-b2-bn-s
Given a sequence
a[1], a[2], ..., a[n], find an array b[1] < b[2] < ... < b[n] such that |a[1]-b[1]| + |a[2]-b[2]| + ... + |a[n]-b[n]| is minimum.
I have already come up with some observations, but I still couldn't figure out any feasible solution.
it is given that
n <= 10^6.
The problem is from BOI 2003, and is called Sequence.
Input
9 4 8 20 14 15 18
Output
6 7 8 13 14 15 18
Since the difference is 13.
Solution:
This problem can be solved by minimum cost flow. Here we use dynamic programming.
Let F(k, z) be the optimal objective value for the first k elements with B[k] = z. Then, we have a recurrence relation: F(k, z) = min F(k-1, x) + |z – A[k]|. Thus, the problem becomes how to efficiently find the z minimizing F(k, z) for all fixed k. It can be showed that F(k, z) is a piecewise linear convex function in z and the minimizing value must be in A. Thus, the dynamic programming can be speed up by using slope optimization and find the solution in O(n lg n) time.
令 F(k, z) 為前 k 個元素且 B[k] = z 時的最佳解之值。當給定 k ，我們可得一遞回關係式：F(k, z) = min F(k-1, x) + |z – A[k]|。因此問題就變成如何快速的找出最小化 F(k, z) 的 z 值。我們可以證明 F(k, z) 對於 z 是一個 piecewise linear convex 函數 ，而且可以最小化 F 的 z 值必定在 A 中。因此使用動態規劃加上斜率最佳化可以在O(n lg n)時間內找到答案。
http://stackoverflow.com/questions/10460861/finding-an-increasing-sequence-a-which-minimizes-sigmaabsaici
Read full article from Isotonic Regression | Algorithms Notes
