Range Minimum Query | iCode
Given an array say A[0,N-1], we are queried for the minimum element from some index 'i' to the index 'j' such that j>=i, the notation for rest of the post for this will be RMQ(i,j) s.t. j>=i.
Ex: A = [3 , 2 , -1 , 4 , 2]
RMQ(0,2) = -1
RMQ(3,4) = 2
RMQ(0,4) = -1
4. Dynamic Programming Approach 2 (Sparse Table)
https://algorithmcafe.wordpress.com/2012/02/04/sparse-table-st-algorithm/
Time Complexity : Construction O(NlogN) Query O(1) <O(NlogN),O(1)>
Segment trees are more popular, because they are more flexible than sparse tables, they can also be used for interval update which is most often clubbed with the interval query in a programming challenges while sparse table can not be used to update the array(as it is based on precomputations).
2. Dynamic Programming Approach 1 (Trivial)
Time Complexity : Construction O(N^2) , Query O(1) <O(N^2),O(1)>
Naive’s Approach
Time Complexity : construction O(1) , Query O(N) <O(1),O(N)>
Read full article from Range Minimum Query | iCode
Given an array say A[0,N-1], we are queried for the minimum element from some index 'i' to the index 'j' such that j>=i, the notation for rest of the post for this will be RMQ(i,j) s.t. j>=i.
Ex: A = [3 , 2 , -1 , 4 , 2]
RMQ(0,2) = -1
RMQ(3,4) = 2
RMQ(0,4) = -1
5. Segment Trees
Time Complexity : Construction O(N) Query O(logN) <O(N),O(logN)>
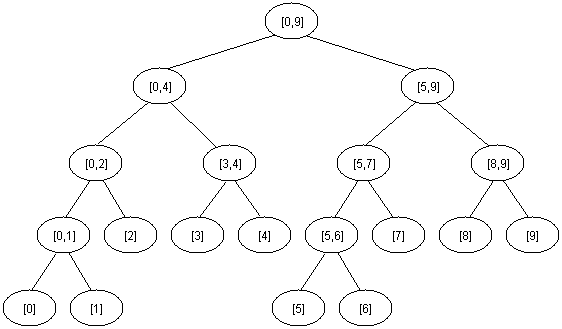
segment tree are one of the most popular and most powerful data structures for interval update and interval queries. Segment trees are mostly preferred over any other methods described above and are useful in most of the programming competitions. Segment trees are heap like data structures. The segment tree for an array of size 10 would look like this.
Time Complexity : Construction O(N) Query O(logN) <O(N),O(logN)>
segment tree are one of the most popular and most powerful data structures for interval update and interval queries. Segment trees are mostly preferred over any other methods described above and are useful in most of the programming competitions. Segment trees are heap like data structures. The segment tree for an array of size 10 would look like this.

Segment tree can be stored in the form of an array of size ‘2^(logN+1)-1’ say M.The left and the right child of node numbered ‘x’ will be ‘2*x+1’ and ‘2*x+2’ respectively.
int M[MAXSIZE];//node is the index of the segment tree m, start and end are the index of the the array Avoid BuildTree(int node,int start,int end,int A[],int N){ if(start==end) M[node]=start; else{ BuildTree(2*node+1,start,(start+end)/2,A,N); BuildTree(2*node+2,(start+end)/2+1,end,A,N); if(A[M[2*node+1]]<A[M[2*node+2]]) M[node]=M[2*node+1]; else M[node]=M[2*node+2]; }}int RMQ(int node,int start,int end,int s,int e,int A[]){ if(s<=start&&e>=end) return M[node]; else if(s>end || e<start) return -1; int q1 = RMQ(2*node+1,start,(start+end)/2,s,e,A); int q2 = RMQ(2*node+2,(start+end)/2+1,end,s,e,A); if(q1==-1) return q2; else if(q2==-1) return q1; if(A[q1]<A[q2]) return q1; return q2;}// driver programmeint main(){ int A[10] = {3,1,2,-1,5,4,6,0,9,8}; BuildTree(0,0,10-1,A,10); int s,e; scanf("%d %d",&s,&e); printf("%d\n",A[RMQ(0,0,10-1,s,e,A)]); return 0;}4. Dynamic Programming Approach 2 (Sparse Table)
https://algorithmcafe.wordpress.com/2012/02/04/sparse-table-st-algorithm/
Time Complexity : Construction O(NlogN) Query O(1) <O(NlogN),O(1)>
parse tables stores the information from one index ‘i’ to the some index ‘j’ which is at a specific distance from ‘i’.
Here we use Sparse table to store the minimum of the elements between index ‘i’ to i+’2^j’. It can be better understood with the help of an example :
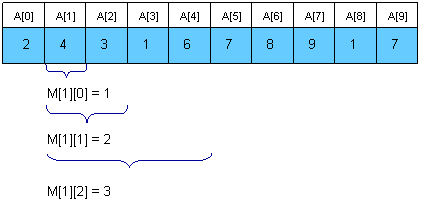
let us say, A = [2,4,3,1,6,7,8,9,1,7]
and the sparse table be two dimensional Array M( N*(log(N)+1) )
let us say, A = [2,4,3,1,6,7,8,9,1,7]
and the sparse table be two dimensional Array M( N*(log(N)+1) )
http://blog.csdn.net/niushuai666/article/details/6624672
http://noalgo.info/489.html
http://noalgo.info/489.html
ST算法本质上是动态规划算法,定义了一个二维辅助数组st[n][n],st[i][j]表示原数组a中从下标i开始,长度为2^j的子数组中的最值(以最小值为例)。
要求解st[i][j]时,即求下标i开始,长度为2^j的子数组的最小值时,可以把这段子数组再划分成两半,每半的长度为2^(j-1),于是前一半的最小值为st[i][j-1],后一半的最小值为st[i+2^(j-1)][j-1],于是动态规划的转移方程为:
st[i][j] = min(st[i][j-1], st[i+2^(j-1)][j-1])
长度为2^j的情况只和长度为2^(j-1)的情况有关,只需要初始化长度为2^0=1的情况即可。而长度为1时的最小值是显然的(为其本身)。
现在问题是,st数组可以怎样加速我们的查询呢?
这也是算法的巧妙之处,假设求下标在u到v之间的最小值。先求u和v之间的长度len=v-u+1,然后求k=log2(len),则u到v之间的子数组可以分为两部分:
- 以u开始,长度为2^k的一段
- 以v结束,长度为2^k的一段(可以计算得到起始位置为v-2^k+1)
注意,一般情况下这两段是重叠的,但是这两段的最小值中较小的一个仍然是u到v的最小值。于是
RMQ(u,v) = min(st[u][k], st[v-2^k+1][k])
有时候需要得到最值的下标而不是最值内容,这时可以使用以下的下标版本。
http://dongxicheng.org/structure/lca-rmq/
首先是预处理,用动态规划(DP)解决。设A[i]是要求区间最值的数列,F[i, j]表示从第i个数起连续2^j个数中的最大值。例如数列3 2 4 5 6 8 1 2 9 7,F[1,0]表示第1个数起,长度为2^0=1的最大值,其实就是3这个数。 F[1,2]=5,F[1,3]=8,F[2,0]=2,F[2,1]=4……从这里可以看出F[i,0]其实就等于A[i]。这样,DP的状态、初值都已经有了,剩下的就是状态转移方程。我们把F[i,j]平均分成两段(因为f[i,j]一定是偶数个数字),从i到i+2^(j-1)-1为一段,i+2^(j-1)到i+2^j-1为一段(长度都为2^(j-1))。用上例说明,当i=1,j=3时就是3,2,4,5 和 6,8,1,2这两段。F[i,j]就是这两段的最大值中的最大值。于是我们得到了动态规划方程F[i, j]=max(F[i,j-1], F[i + 2^(j-1),j-1])。
然后是查询。取k=[log2(j-i+1)],则有:RMQ(A, i, j)=min{F[i,k],F[j-2^k+1,k]}。 举例说明,要求区间[2,8]的最大值,就要把它分成[2,5]和[5,8]两个区间,因为这两个区间的最大值我们可以直接由f[2,2]和f[5,2]得到
To compute M[i][j] we use dynamic programming
M[i][j-1] if(A[M[i][j-1]]<= A[M[i+2^(j-1)-1][j-1]])
M[i][j] =
M[i+2^(j-1)-1][j-1]
Now after precomputation of the table ‘M’ The RMQ can be solved in O(1) as follows :
let k = log(j-i+1)
let k = log(j-i+1)
A[M[i][k]] if(A[M[i][k]]<=A[M[j-2^k+1][k]])
RMQ(i,j) =
A[M[j-2^k+1][k]]
int M[MAXN][MAXLOGN];void Compute_ST(int A[],int N){ int i,j; for(i=0;i<N;i++) M[i][0]=i; for(j=1;1<<j <=N ;j++){ for(i=0;i+(1<<(j-1))<N;i++){ if(A[M[i][j-1]]<=A[M[i+(1<<(j-1))][j-1]]) M[i][j]=M[i][j-1]; else M[i][j]=M[i+(1<<(j-1))][j-1]; } }}int RMQ(int A[],int s,int e){ int k=e-s; k=31-__builtin_clz(k+1); // k = log(e-s+1) if(A[M[s][k]]<=A[M[e-(1<<k)+1][k]]) return A[M[s][k]]; return A[M[e-(1<<k)+1][k]];}Segment trees are more popular, because they are more flexible than sparse tables, they can also be used for interval update which is most often clubbed with the interval query in a programming challenges while sparse table can not be used to update the array(as it is based on precomputations).
3. Split and Query
Time Complexity : construction O(N) , Query O(sqrt(N)) <O(N),O(sqrt(N))>
Here we split the array in sqrt(N) equal parts of size sqrt(N), The idea is to store the minimum of each part in the an another array say M(0*sqrt(N)), and then for every query we traverse the array ‘M’ and the remaining elements of the array A.
Let us understand through an example :
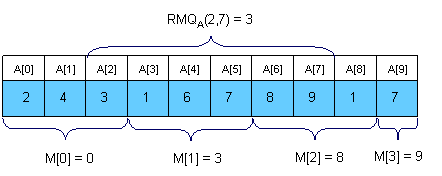
A = [2,4,3,1,6,7,8,9,1,7]
Time Complexity : construction O(N) , Query O(sqrt(N)) <O(N),O(sqrt(N))>
Here we split the array in sqrt(N) equal parts of size sqrt(N), The idea is to store the minimum of each part in the an another array say M(0*sqrt(N)), and then for every query we traverse the array ‘M’ and the remaining elements of the array A.
Let us understand through an example :
A = [2,4,3,1,6,7,8,9,1,7]
as it is clear from the image that M[0] is storing the index of the minimum element from A[0] to A[2] then M[1] will store index of the minimum element from A[3] to A[5] … ans so on till it is M[3] which will store A[9] as there are no further elements.
int M[MAXN]; /* M[i] = the index of the minimum element from A[i*sqrt(N)] to A[i*sqrt(N)+sqrt(N)-1] */int size_m; // stores the size of the M arrayvoid RMQ_SPLIT(int A[],int N){ size_m =0; for(int i=0;i<N;){ int minindex = i; for(int j=0;j<(int)sqrt(N) && i<N;j++){ if(A[i]<A[minindex]) minindex=i; i++; } M[size_m++]=minindex; }}int RMQ(int A[],int s,int e,int N){ int start = s/(int)sqrt(N); // this will compute the starting index of the M array int ans = A[s]; int end = e/(int)sqrt(N); // ending index of the M array for(int i=s;i<(start+1)*sqrt(N);i++) if(A[i]<ans) ans = A[i]; for(int i=start+1;i<end;i++){ if(A[M[i]]<ans) ans=A[M[i]]; } for(int i=end*sqrt(N);i<=e;i++){ if(A[i]<ans) ans = A[i]; } return ans;}2. Dynamic Programming Approach 1 (Trivial)
Time Complexity : Construction O(N^2) , Query O(1) <O(N^2),O(1)>
j, if A[j] < A[M[i][j-1]]
M[i][j]=
M[i][j-1], otherwise
int RMQ_DP(int A[],int N){ for(int i=0;i<N;i++) M[i][i]=i; for(int i=0;i<N;i++){ for(int j=i+1;<N;j++){ if(A[M[i][j-1]]>A[j]) M[i][j]=j; else M[i][j]=M[i][j-1]; } }} printf("%d\n",A[M[s][e]]);Naive’s Approach
Time Complexity : construction O(1) , Query O(N) <O(1),O(N)>
int RMQ(int A[],int s,int e){ int minindex = s; for(int i=s;i<=e;i++) if(A[i]&<A[minindex]) minindex = i; return A[minindex];}Read full article from Range Minimum Query | iCode