https://www.luogu.org/problemnew/show/P3084

f[i]f[i]表示到第i个位置且第i个位置必放最多能放多少个点。
对于每个位置,他前一个能放置的位置应该是满足一个区间的。
因为一个区间中只能有一个点,所以包含这个点的所有区间都不能再放,就是要找到包含这个点的区间中左端点最小的位置,R[i]=位置-1
因为每个区间都必须有一个点,所以不能有区间空着不放。找到整个区间完全在当前点之前且左端点最大的区间,L[i]=该区间的左端点。
怎么统计L,R,每次加入一个区间[x,y],就用x更新L[y+1],x-1更新R[y].最后从小到大扫一遍,每个位置的L对前缀最小值取max;从大到小扫一遍,每个位置的R对后缀最小值取min
那么f[i]=max{f[j],L[i]<=j<=R[i]}+1f[i]=max{f[j],L[i]<=j<=R[i]}+1,可以用单调队列优化。
https://blog.csdn.net/largecub233/article/details/78288863
f[i]表示到igxe点切i点有一头斑点牛的最大值
显然有些位置是一定不能放斑点牛的;
那么对于可以放牛的i点我们有2个限制
每一个区间最多一头奶牛
每一个区间最少一头奶牛
这两个限制让我们发现了一个区间
有第一个限制我萌可以得到这个区间的右端点为所有覆盖i点的区间里的min(左端点)
第二个限制我们可以得到这个区间的左端点为所有没覆盖i点的区间里的max(左端点)
这个区间里的j才可以更新f[i]
f[i]=f[j]+1//f[j]!=-1
因为我们在这个区间里放一奶牛,才不适破坏限制;
那么之后我们只要去一个区间最大值就好啦
单调dp可以很好的做到这一点;
https://www.cnblogs.com/liutianrui/p/7588467.html
Farmer John has decided to assemble a panoramic photo of a lineup of his N cows (1 <= N <= 200,000), which, as always, are conveniently numbered from 1..N. Accordingly, he snapped M (1 <= M <= 100,000) photos, each covering a contiguous range of cows: photo i contains cows a_i through b_i inclusive. The photos collectively may not necessarily cover every single cow.
After taking his photos, FJ notices a very interesting phenomenon: each photo he took contains exactly one cow with spots! FJ was aware that he had some number of spotted cows in his herd, but he had never actually counted them. Based on his photos, please determine the maximum possible number of spotted cows that could exist in his herd. Output -1 if there is no possible assignment of spots to cows consistent with FJ's photographic results.
农夫约翰决定给站在一条线上的N(1 <= N <= 200,000)头奶牛制作一张全家福照片,N头奶牛编号1到N。
于是约翰拍摄了M(1 <= M <= 100,000)张照片,每张照片都覆盖了连续一段奶牛:第i张照片中包含了编号a_i 到 b_i的奶牛。但是这些照片不一定把每一只奶牛都拍了进去。
在拍完照片后,约翰发现了一个有趣的事情:每张照片中都有且仅有一只身上带有斑点的奶牛。约翰意识到他的牛群中有一些斑点奶牛,但他从来没有统计过它们的数量。 根据照片,请你帮约翰估算在他的牛群中最多可能有多少只斑点奶牛。如果无解,输出“-1”。
https://www.cnblogs.com/lyzuikeai/p/7566740.html
给你一个n长度的数轴和m个区间,每个区间里有且仅有一个点,问能有多少个点
Input
* Line 1: Two integers N and M.
* Lines 2..M+1: Line i+1 contains a_i and b_i.
Output
* Line 1: The maximum possible number of spotted cows on FJ's farm, or -1 if there is no possible solution.
Sample Input
5 3
1 4
2 5
3 4
INPUT DETAILS: There are 5 cows and 3 photos. The first photo contains cows 1 through 4, etc.
1 4
2 5
3 4
INPUT DETAILS: There are 5 cows and 3 photos. The first photo contains cows 1 through 4, etc.
Sample Output
1
OUTPUT DETAILS: From the last photo, we know that either cow 3 or cow 4 must be spotted.
OUTPUT DETAILS: From the last photo, we know that either cow 3 or cow 4 must be spotted.
By choosing either of these, we satisfy the first two photos as well.
There are 5 cows and 3 photos. The first photo contains cows 1 through 4, etc.
From the last photo, we know that either cow 3 or cow 4 must be spotted. By choosing either of these, we satisfy the first two photos as well.
——————————————————————————————————
我们用f[i]表示选i这个位置放置特殊点的最优解
那么我们发现每个点可以选择的范围是一个区间
并且容易证明这个区间是随着位置的增加而右移也就是单调递增的
因为你选择了这个点 那么包含这个点的所有区间都不能再加点了
所以r【i】=min(包含i的区间的左端点-1)
因为每个区间都要有点所以l【i】=完整在i左边的区间中左端点的max
这样我们就得到了每个点的转移区间
这样完美符合单调队列的性质 所以就可以写了
https://www.cnblogs.com/Chorolop/p/7570191.html
先说分类:DP,单调队列优化DP
合理性:
状态表示为 F[ i ],表示只考虑前 i 只奶牛,且第 i 只奶牛必取,特殊情况下对 F[ i ] 取特殊值以区分
显然这样是没有后效性的
因此整个主线就基本明朗了:后面的继承前面的
那么就有一个被继承的区域,我们在这个区域里面选择最大值继承
好吧,根据题目,我们知道
每张照片里面 仅有且必有 一只有斑点的奶牛
那么我们继承就有这么个原则了:
1. 每个区间都必须要取一个点,可以共用;
2. 每个区间内不能重复取点
那么继承从距离 i 当前区间最近的左边的那个区间开始,直到 i 当前这个区间的最左的左端点结束

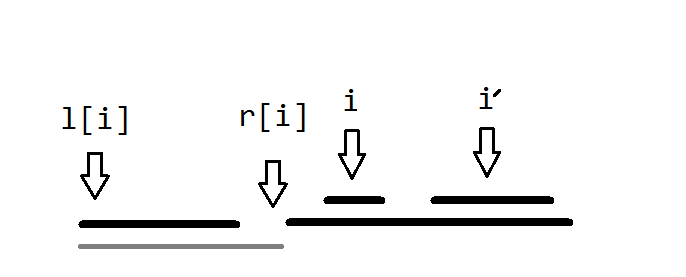
你看,点 i 可以是被多个区间所包围的。
我们所说的左边最近的区间,这个时候 i 的区间指的是最小的 i 的区间,也就是上图包括 i 点的最顶上的那个小区间
那么对 i 而言,这个左边最近的区间指的是图片最左端这块飞地;而对于 i‘ ,这个左边最近指的就是 i 的区间了
在继承过程中,我们需要考虑到每一个区间,因为每一张照片都必有一个奶牛,如果这里不是最小的区间的话,很可能会漏掉某些区间
而对于最左的左端点则是包围 i 点的最大的区间的左端点,因为在一个区间里只能取一个点,而被继承的那个点是必取的
所以我们得到了百度到的一堆题解的那个核心结论:
对于点 i ,它的继承区间是:从 所在区间左边最近的区间的左端点 起,至 所在区间的最左的左端点-1 结束
对于一个点怎么迅速找到它的继承区间呢?
这= =
显然看解题人数感了
我只能做到解释其合理性
1 for(int i = 1;i <= n+1;i++) r[i] = i-1; 2 3 for(int i = 1;i <= m;i++){ 4 scanf("%d%d",&a,&b); 5 r[b] = min(r[b],a-1); 6 l[b+1] = max(l[b+1],a); 7 } 8 9 for(int i = n;i;i--) 10 r[i] = min(r[i],r[i+1]); 11 12 for(int i = 2;i <= n+1;i++) 13 l[i] = max(l[i],l[i-1]);
读入一段区间时,我们就可以更新至少两个点的继承区间值了:b+1 和 b
对于b+1,无疑区间[a,b]是它左边最近的一个区间,可以更新它的继承区间左端点;
对于b,还有[a,b]里的所有的点,他们的继承区间右端点都可以以a-1为值更新,但是这里只更新b一个点,事后可以O(n)
那么对于每个点的继承区间右端点,我们从右往左扫意味着一件事情:右边的点可以改变左边,左边的点不能更新右边

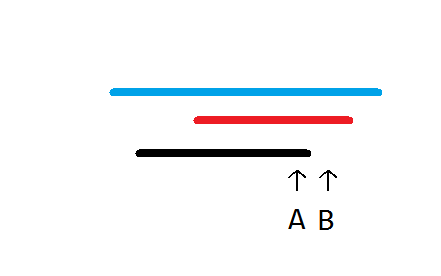
其中红线蓝线都是B的待选区间,不同时存在
当B的区间是红线的时候,B可以继承红线和黑线不重叠的地方
而A的继承区间会终止于黑线后,结果对的!
当B的区间是蓝线的时候,显然A会拿B的取值去更新,也是对的!
对于继承区间的左端点的O(n)更新,和右端点取值同理,自行思考即可
巧妙运用了某些值取值的单调性
qwq这才是算法功底好的体现啊
那么在DP的时候我们的方向就很明确了:
对于每个点,从它的继承区间里继承就行了,需要不停地扫,目测n方
而我们要取的是区间里的最大值
那么这个时候滑动窗口就发挥作用了:
如果当前这个考虑的被继承点 j 的DP值小于我们已经知道的最大值,就没必要考虑了
而对于那些已经不在继承区间里却仍然被保存的值,也没必要考虑了
因此来一波单调队列,在代码里是单调队列维护最大值,这个解释清楚了估计就很容易理解了
现在来考虑非法情况,还是就上面那张图片:

非法情况,就是 i 和 i’ 这样子的,两个区间被一个大区间包括,那么这个大区间里必须要选两个点
这个时候,我们把该点置为非法,也就是-inf
并且从这个第一次出现非法情况的 i‘ 所在的区间开始,之后每一个点都会是非法点,这个非法值会延续到最后一个点
因为对于处于大区间的点,非法区间及以后的点他们的继承区间左右端点是非法的,右端点小于左端点,包含了一个空集
你看,i’ 区间内的点,右端点是大区间的左端点-1,左端点却是 i 区间的左端点
而出了 i‘ 区间,右端点依然是大区间的左端点,左端点是 i’ 的左端点,持续非法
而出了大区间,第一个点是大区间右端点+1,叫他A点
A点的左端点是 i‘ 左端点,右端点根据初始化是A-1,而这里所有的值都是非法值
之后也显然没法再取到一个正常的值了
综上可证该算法中非法值有持续性和覆盖性
另外再说结尾是n+1的原因
我们对DP[ i ] 的定义是必取 i 的情况
但是我们不一定取 n 为斑点奶牛
所以我们要选择n+1
15 int n,m,a,b,r[maxn],l[maxn],DP[maxn]; 16 int que[maxn],head,tail; 17 18 int main(){ 19 scanf("%d%d",&n,&m); 20 21 for(int i = 1;i <= n+1;i++) r[i] = i-1; 22 23 for(int i = 1;i <= m;i++){ 24 scanf("%d%d",&a,&b); 25 r[b] = min(r[b],a-1); 26 l[b+1] = max(l[b+1],a); 27 } 28 29 for(int i = n;i;i--) 30 r[i] = min(r[i],r[i+1]); 31 32 for(int i = 2;i <= n+1;i++) 33 l[i] = max(l[i],l[i-1]); 34 35 for(int i = 1;i <= n+1;i++){ 36 for(int k = l[i];k <= r[i];k++){ 37 while(tail < head && DP[que[head]] <= DP[k]) head--; 38 que[++head] = k; 39 } 40 41 while(tail < head && que[tail+1] < l[i]) tail++; 42 43 if(tail == head) DP[i] = -1e9; 44 else DP[i] = DP[que[tail+1]] +1; 45 } 46 47 // for(int i = 0;i <= n+1;i++) printf("%d ",DP[i]); 48 // cout << endl; 49 50 if(DP[n+1] >= 0) printf("%d\n",DP[n+1]-1); 51 else printf("-1\n"); 52 53 return 0; 54 }https://blog.csdn.net/clover_hxy/article/details/72763202
f[i]f[i]表示到第i个位置且第i个位置必放最多能放多少个点。
对于每个位置,他前一个能放置的位置应该是满足一个区间的。
因为一个区间中只能有一个点,所以包含这个点的所有区间都不能再放,就是要找到包含这个点的区间中左端点最小的位置,R[i]=位置-1
因为每个区间都必须有一个点,所以不能有区间空着不放。找到整个区间完全在当前点之前且左端点最大的区间,L[i]=该区间的左端点。
怎么统计L,R,每次加入一个区间[x,y],就用x更新L[y+1],x-1更新R[y].最后从小到大扫一遍,每个位置的L对前缀最小值取max;从大到小扫一遍,每个位置的R对后缀最小值取min
那么f[i]=max{f[j],L[i]<=j<=R[i]}+1f[i]=max{f[j],L[i]<=j<=R[i]}+1,可以用单调队列优化。
https://blog.csdn.net/largecub233/article/details/78288863
f[i]表示到igxe点切i点有一头斑点牛的最大值
显然有些位置是一定不能放斑点牛的;
那么对于可以放牛的i点我们有2个限制
每一个区间最多一头奶牛
每一个区间最少一头奶牛
这两个限制让我们发现了一个区间
有第一个限制我萌可以得到这个区间的右端点为所有覆盖i点的区间里的min(左端点)
第二个限制我们可以得到这个区间的左端点为所有没覆盖i点的区间里的max(左端点)
这个区间里的j才可以更新f[i]
f[i]=f[j]+1//f[j]!=-1
因为我们在这个区间里放一奶牛,才不适破坏限制;
那么之后我们只要去一个区间最大值就好啦
单调dp可以很好的做到这一点;
https://www.cnblogs.com/liutianrui/p/7588467.html
这道题更多的是偏向于动归题,如果知道是动归的话那么转移方程一般也就写的出来了:
f[i]=MAX(f[j])+1
看着挺简单的,但是j的取值范围的确定是这道题的关键,为此我们可以在纸上自己模拟一些情况,然后我们可以注意到,能够更新这个点且合法的点一定在离当前点最近的完整区间的左端点及其之后,且一定在离当前点最近的右端点之前。而我们又发现这个区间对于每个点都是单调的,所以我们可以打出来单调队列来进行优化。因此这道题就差不多搞完了。
最后一点,不合法的情况的判断。如果说当前点的可选取的左边界大于右边界,那么,这个点我们是不能去放置的,我们应把它赋为极小值,注意,此时只是在这个点放置不合法,不代表整个题都不合法。而如果出现了对于整个题目设置都不合法的情况他后面的区间都会受他影响而变为负值
