https://www.jianshu.com/p/dabdf25ffc67
http://www.cnblogs.com/CzYoL/p/7253499.html
https://blog.csdn.net/Clove_unique/article/details/50506266
烽火台又称烽燧,是重要的防御设施,一般建在险要处或交通要道上。一旦有敌情发生,白天燃烧柴草,通过浓烟表达信息:夜晚燃烧干柴,以火光传递军情。在某两座城市之间有n个烽火台,每个烽火台发出信号都有一定的代价。为了使情报准确的传递,在m个烽火台中至少要有一个发出信号。现输入n、m和每个烽火台发出的信号的代价,请计算总共最少需要花费多少代价,才能使敌军来袭之时,情报能在这两座城市之间准确的传递!!!
输入格式 Input Format
第一行有两个数n,m分别表示n个烽火台,在m个烽火台中至少要有一个发出信号。
第二行为n个数,表示每一个烽火台的代价。
输出格式 Output Format
一个数,即最小代价。
样例
5 3
1 2 5 6 2
4
时间限制 Time Limitation
各个测试点1s
注释 Hint
1<=n,m<=1,000,000
https://blog.csdn.net/er111er/article/details/78344161
分析题目,由于题目要求连续m个烽火台中至少要有一个发出信号,很容易得出DP转移方程:
F[i]=min(F[j]:i−m<j<i)+a[i]F[i]=min(F[j]:i−m<j<i)+a[i]
最直接的方法是枚举状态,对于每一个i,我们在i-m+1到i-1中寻找一个最小的F[j]进行状态转移,枚举状态的时间复杂度是O(n),寻找最小值的状态时间复杂度是O(n),因此这种方法的复杂度是O(n^2)。题目的是数据范围是n<=100000,显然超时。
那么怎么用单调队列优化呢?
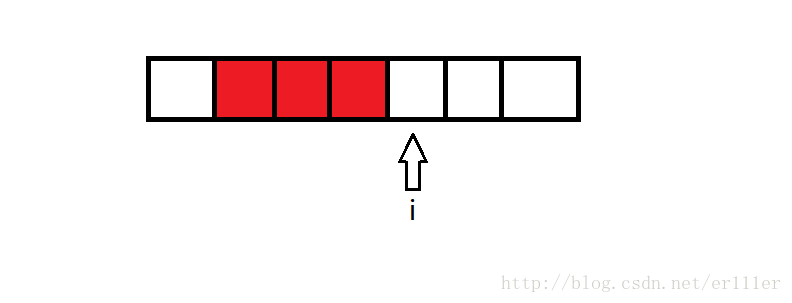
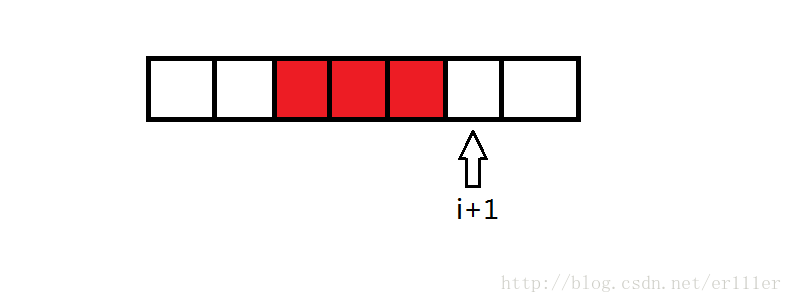
上图中,状态枚举到i,当m=4时,我们要做的就是在i-3到i-1中找到最小的F[j],那么枚举到i+1时,我们要做的就是要在i-2到i中找到最小的F[j]。上图中我们可以看出,要寻找最小值的区间向后移动了一位,也就是F[i-m+1]的值被抛弃,F[i-1]的值被加入。这里就可以用单调队列处理了,F[i-1]是插队的数据,F[i-1]有资格插队是因为它更优且更靠近i,比它更差的数将被它取代,保留那些数据没有任何好处。而那些已经不再维护区间之外的就不必再对其进行维护,出队即可。看了代码会更加明白:
int main()
{
freopen("beacon.in", "r", stdin);
freopen("beacon.out", "w", stdout);
scanf("%d%d", &n, &m);
for (int i = 1;i <= n;i++)
scanf("%d", &a[i]);
for (int i = 1;i <= n;i++)
{
while (head <= tail && f[i - 1] <= f[que[tail]]) tail--; //当F[i-1]比队尾值更优时把队尾值弹出
que[++tail] = i - 1; //把F[i-1]插入,这里插入下标而不插入值,便于从队头弹出
while (head <= tail && que[head] < i - m) head++; //不属于区间维护内的数弹出
f[i] = f[que[head]] + a[i]; //状态转移
}
for (int i = n;i > n - m;i--) //求出答案
ans = min(ans, f[i]);
printf("%d\n", ans);
fclose(stdin);
fclose(stdout);
return 0;
}
https://5261.github.io/article/SignalFire-transmit/
即考虑前一个烽火台的位置。
要用动态规划的方法解决。我们可以写出这样的方程f[i]:=min{f[j]}+a[i] (i-m<=j<=i-1)
我们想到了用单调队列进行优化,由于随着i的循环,每次只有一个i进入决策区间也只有一个i出决策区间,由于每次选取决策区间中的最小值,所以维护一个单调递增序列,每次取出队首元素即可。
为什么可以将队尾元素无情的删去呢?由于后进队的序列同时满足在原序列中的位置更靠后和其在动态规划中的价值更大。这样选取这个元素就要比选取之前的任何一个决策要优,所以之前被删掉的决策都是无用的。
这道题的本质就是用单调队列维护了决策本身的价值和其在原序列中位置的同时单调。
要特别注意单调队列中的值是决策在原决策序列中的位置。
补充:
设f[i]表示点燃当前位置烽火台,且前i个满足要求的最小代价。
显然就有f[i]=min(f[j])+a[i](i-m<=j<=i-1)。
当然,这会超时,所以要有优化。
优化一:肯定是从前m个里选小的,涉及到区间最小值,可用线段树,时间复杂度将为O(n log m)。
优化二:同样因为要选前m个最小的,使用单调队列,队列里存有不超过m个长度单位的值,每次取队首,进队时维护队列使其单调不下降,复杂度将为O(n)。
输入格式 Input Format
第一行有两个数n,m分别表示n个烽火台,在m个烽火台中至少要有一个发出信号。
第二行为n个数,表示每一个烽火台的代价。
输出格式 Output Format
一个数,即最小代价。
样例
5 3
1 2 5 6 2
4
时间限制 Time Limitation
各个测试点1s
注释 Hint
1<=n,m<=1,000,000
https://blog.csdn.net/er111er/article/details/78344161
分析题目,由于题目要求连续m个烽火台中至少要有一个发出信号,很容易得出DP转移方程:
F[i]=min(F[j]:i−m<j<i)+a[i]F[i]=min(F[j]:i−m<j<i)+a[i]
最直接的方法是枚举状态,对于每一个i,我们在i-m+1到i-1中寻找一个最小的F[j]进行状态转移,枚举状态的时间复杂度是O(n),寻找最小值的状态时间复杂度是O(n),因此这种方法的复杂度是O(n^2)。题目的是数据范围是n<=100000,显然超时。
那么怎么用单调队列优化呢?
上图中,状态枚举到i,当m=4时,我们要做的就是在i-3到i-1中找到最小的F[j],那么枚举到i+1时,我们要做的就是要在i-2到i中找到最小的F[j]。上图中我们可以看出,要寻找最小值的区间向后移动了一位,也就是F[i-m+1]的值被抛弃,F[i-1]的值被加入。这里就可以用单调队列处理了,F[i-1]是插队的数据,F[i-1]有资格插队是因为它更优且更靠近i,比它更差的数将被它取代,保留那些数据没有任何好处。而那些已经不再维护区间之外的就不必再对其进行维护,出队即可。看了代码会更加明白:
int main()
{
freopen("beacon.in", "r", stdin);
freopen("beacon.out", "w", stdout);
scanf("%d%d", &n, &m);
for (int i = 1;i <= n;i++)
scanf("%d", &a[i]);
for (int i = 1;i <= n;i++)
{
while (head <= tail && f[i - 1] <= f[que[tail]]) tail--; //当F[i-1]比队尾值更优时把队尾值弹出
que[++tail] = i - 1; //把F[i-1]插入,这里插入下标而不插入值,便于从队头弹出
while (head <= tail && que[head] < i - m) head++; //不属于区间维护内的数弹出
f[i] = f[que[head]] + a[i]; //状态转移
}
for (int i = n;i > n - m;i--) //求出答案
ans = min(ans, f[i]);
printf("%d\n", ans);
fclose(stdin);
fclose(stdout);
return 0;
}
https://5261.github.io/article/SignalFire-transmit/
动态规划,设表示在中传递情报,且烽火台必须参与传递的最小代价。
转移:
上式在计算时需要区间最小值,且决策区间是向右平移的 。
因此我们使用单调队列来优化。
考虑到要保证情报的传递,答案为:
要用动态规划的方法解决。我们可以写出这样的方程f[i]:=min{f[j]}+a[i] (i-m<=j<=i-1)
我们想到了用单调队列进行优化,由于随着i的循环,每次只有一个i进入决策区间也只有一个i出决策区间,由于每次选取决策区间中的最小值,所以维护一个单调递增序列,每次取出队首元素即可。
为什么可以将队尾元素无情的删去呢?由于后进队的序列同时满足在原序列中的位置更靠后和其在动态规划中的价值更大。这样选取这个元素就要比选取之前的任何一个决策要优,所以之前被删掉的决策都是无用的。
这道题的本质就是用单调队列维护了决策本身的价值和其在原序列中位置的同时单调。
要特别注意单调队列中的值是决策在原决策序列中的位置。
补充:
设f[i]表示点燃当前位置烽火台,且前i个满足要求的最小代价。
显然就有f[i]=min(f[j])+a[i](i-m<=j<=i-1)。
当然,这会超时,所以要有优化。
优化一:肯定是从前m个里选小的,涉及到区间最小值,可用线段树,时间复杂度将为O(n log m)。
优化二:同样因为要选前m个最小的,使用单调队列,队列里存有不超过m个长度单位的值,每次取队首,进队时维护队列使其单调不下降,复杂度将为O(n)。
首先考虑dp,因为每m个点中必须选择2个,那么对于当前点(i),
这样的每次要去寻找最小值,复杂度报表,考虑dp优化。
由于要取最小值,那么就可以维护一个单调递增的单调队列,每次入队维护单调性,并删除队首不在区间中的数,然后队首就是要找的最小值。
这样下来,时间复杂度
struct node{ int val, id;};node que[N];int cost[N], head, tail, i, f[N];int n, m;int main(){ n = read(), m = read(); for(i = 1; i <= n; i++) cost[i] = read(); head = 1, tail = 1; for(i = 1; i <= n; i++){ while(que[head].id < i - m && head <= tail) head++; f[i] = que[head].val + cost[i]; while(tail >= head && que[tail].val >= f[i]) tail--; que[++tail] = (node){f[i], i};// for(int j = head; j <= tail; j++) cout<<que[j].val<<" ";cout<<endl; } int ans = oo; for(int i = n - m + 1; i <= n; i++) ans = min(ans, f[i]); cout<<ans<<endl; return 0;} |
再说一下细节问题:
①先调整单调队列的范围,再更新当前的f
②可选与不可选的范围要注意
③状态的表示决定了最后需要枚举最小值,但是这个枚举必须从n-m+1开始,因为最后m个里必选一个
int n,m,head,tail,Min;
int queue[1000005],a[1000005],f[1000005];
int main(){
scanf("%d%d",&n,&m);
for (int i=1;i<=n;++i) scanf("%d",&a[i]);
for (int i=1;i<=n;++i){
while (queue[head]<i-m&&head<=tail) head++;
f[i]=a[i]+f[queue[head]];
while (f[queue[tail]]>f[i]&&head<=tail) tail--;
queue[++tail]=i;
}
Min=inf;
for (int i=n-m+1;i<=n;++i)
Min=min(Min,f[i]);
printf("%d\n",Min);
因为二重循环的时间复杂度是O(nm)所以会爆
SO我们维护一个小根堆(好吧我承认我不知道单调队列),把F数组的元素放进去,每次拿走堆顶元素直到该元素符合要求。
为了满足所有位置,最后答案是min(F[i]) (i=n-m+1~n)