LeetCode 689 - Maximum Sum of 3 Non-Overlapping Subarrays

Related: Lintcode 43 - Maximum Subarray III
Related: Lintcode 41,42 - Maximum Subarray I,II
https://leetcode.com/problems/maximum-sum-of-3-non-overlapping-subarrays/

In a given array nums of positive integers, find three non-overlapping subarrays with maximum sum.

Each subarray will be of size k, and we want to maximize the sum of all 3*k entries.

Return the result as a list of indices representing the starting position of each interval (0-indexed). If there are multiple answers, return the lexicographically smallest one.

Example:

Input: [1,2,1,2,6,7,5,1], 2
Output: [0, 3, 5]
Explanation: Subarrays [1, 2], [2, 6], [7, 5] correspond to the starting indices [0, 3, 5].
We could have also taken [2, 1], but an answer of [1, 3, 5] would be lexicographically larger.

Note:

nums.length will be between 1 and 20000.

nums[i] will be between 1 and 65535.

k will be between 1 and floor(nums.length / 3)

http://www.cnblogs.com/grandyang/p/8453386.html

这道题给了我们一个只包含正数的数组，让我们找三个长度为k的不重叠的子数组，使得所有子数组的数字之和最大。首先我们应该明确的是，暴力搜索在这道题上基本不太可能，因为遍历一个子数组的复杂度是平方级，遍历三个还不得六次方啊，看OJ不削你～那么我们只能另辟蹊径，对于这种求子数组和有关的题目时，一般都需要建立累加和数组，为啥呢，因为累加和数组可以快速的求出任意长度的子数组之和，当然也能快速的求出长度为k的子数组之和。因为这道题只让我们找出三个子数组，那么我们可以先确定中间那个子数组的位置，这样左右两边的子数组的位置范围就缩小了，中间子数组的起点不能是从开头到结尾整个区间，必须要在首尾各留出k个位置给其他两个数组。一旦中间子数组的起始位置确定了，那么其和就能通过累加和数组快速确定。那么现在就要在左右两边的区间内分别找出和最大的子数组，遍历所有的子数组显然不是很高效，如何快速求出呢，这里我们需要使用动态规划Dynamic Programming的思想来维护两个DP数组left和right，其中:

left[i]表示在区间[0, i]范围内长度为k且和最大的子数组的起始位置

right[i]表示在区间[i, n - 1]范围内长度为k且和最大的子数组的起始位置

这两个dp数组各需要一个for循环来更新，left数组都初始化为0，前k个数字没办法，肯定起点都是0，变量total初始化为前k个数字之和，然后从第k+1个数字开始，每次向前取k个，利用累加和数组sums快速算出数字之和，跟total比较，如果大于total的话，那么更新total和left数组当前位置值，否则的话left数组的当前值就赋值为前一位的值。同理对right数组的更新也类似，total初始化为最后k个数字之和，然后从前一个数字向前遍历，如果大于total，更新total和right数组的当前位置，否则right数组的当前值就赋值为后一位的值。一旦left数组和right数组都更新好了，那么就可以遍历中间子数组的起始位置了，然后我们可以通过left和right数组快速定位出左边和右边的最大子数组的起始位置，并快速计算出这三个子数组的所有数字之和，用来更新全局最大值mx，如果mx被更新了的话，记录此时的三个子数组的起始位置到结果res中

https://leetcode.com/problems/maximum-sum-of-3-non-overlapping-subarrays/discuss/108231/C%2B%2BJava-DP-with-explanation-O(n)

Great idea to fix the middle index first!

The question asks for three non-overlapping intervals with maximum sum of all 3 intervals. If the middle interval is [i, i+k-1], where k <= i <= n-2k, the left interval has to be in subrange [0, i-1], and the right interval is from subrange [i+k, n-1].

So the following solution is based on DP.

posLeft[i] is the starting index for the left interval in range [0, i];
posRight[i] is the starting index for the right interval in range [i, n-1]; 

Then we test every possible starting index of middle interval, i.e. k <= i <= n-2k, and we can get the corresponding left and right max sum intervals easily from DP. And the run time is O(n).

Caution. In order to get lexicographical smallest order, when there are two intervals with equal max sum, always select the left most one. So in the code, the if condition is ">= tot" for right interval due to backward searching, and "> tot" for left interval

    public int[] maxSumOfThreeSubarrays(int[] nums, int k) {
        int n = nums.length, maxsum = 0;
        int[] sum = new int[n+1], posLeft = new int[n], posRight = new int[n], ans = new int[3];
        for (int i = 0; i < n; i++) sum[i+1] = sum[i]+nums[i];
        // DP for starting index of the left max sum interval
        for (int i = k, tot = sum[k]-sum[0]; i < n; i++) {
            if (sum[i+1]-sum[i+1-k] > tot) {
                posLeft[i] = i+1-k;
                tot = sum[i+1]-sum[i+1-k];
            }
            else
                posLeft[i] = posLeft[i-1];
        }
        // DP for starting index of the right max sum interval
       // caution: the condition is ">= tot" for right interval, and "> tot" for left interval
        posRight[n-k] = n-k;
        for (int i = n-k-1, tot = sum[n]-sum[n-k]; i >= 0; i--) {
            if (sum[i+k]-sum[i] >= tot) {
                posRight[i] = i;
                tot = sum[i+k]-sum[i];
            }
            else
                posRight[i] = posRight[i+1];
        }
        // test all possible middle interval
        for (int i = k; i <= n-2*k; i++) {
            int l = posLeft[i-1], r = posRight[i+k];
            int tot = (sum[i+k]-sum[i]) + (sum[l+k]-sum[l]) + (sum[r+k]-sum[r]);
            if (tot > maxsum) {
                maxsum = tot;
                ans[0] = l; ans[1] = i; ans[2] = r;
            }
        }
        return ans;
    }

https://github.com/YaokaiYang-assaultmaster/LeetCode/blob/master/LeetcodeAlgorithmQuestions/689.%20Maximum%20Sum%20of%203%20Non-Overlapping%20Subarrays.md

This question asks for the three non-overlapping intervals with maximum sum. So this can be divided into 3 parts -- find 3 non-overlapping intervals respectively， and combining the results to get the 3 non-overlapping intervals we want. Since each interval is of length k, suppose the start index of the middle interval is i, then the range of i's value is: k <=i <= n-2k. Actually this i has also indicated the limits of the range of the first interval and the range of the last interval. Hence we have the following DP components:
left[i] stores the start index for the first interval in range [0, i]
right[i] stores the start index for the third interval in range [i, n - 1]


After that we can test every possible start index of middle interval， i.e. k <= i <= n - 2k. And based on the above 2 DP results, we can easily get the first and third max sum intervals. The runtime of this process is O(n).

Note that this question asks for the lexicographical smallest order interval, that is, when there are two intervals with the same max sum, we always select the leftmost one. So in this solution, for the first interval, since we are iterating from left to right, the comparison if statement use currSum > total. And for the third interval, we are iterating from right to left, the comparison if statement use currSum >= total.

Another trick we use here, to ensure the algorithm runs in O(n) time, is that we use predix sum to get the sum of a consecutive subarray in O(1) time. Otherwise, if we calaulate the interval sum each time, that would be O(k) time for each interval.


  public int[] maxSumOfThreeSubarrays(int[] nums, int k) {

    int n = nums.length;

    int[] sum = new int[n + 1];

    int[] left = new int[n];

    int[] right = new int[n];

    int[] ret = new int[3];



    // First get the prefix sum of nums.

    // Prefix sum enables us to get the sum of k consecutive element in O(1) time

    for (int i = 0; i < n; i++) {

      sum[i + 1] = sum[i] + nums[i];

    }



    // DP for the left intetval max sum

    for (int i = k, tot = sum[k] - sum[0]; i < n; i++) {

      if (sum[i + 1] - sum[i - k + 1] > tot) {

        tot = sum[i + 1] - sum[i - k + 1];

        left[i] = i - k + 1;

      } else {

        left[i] = left[i - 1];

      }

    }



    // DP for the right interval max sum

    right[n - k] = n - k;

    for (int i = n - 1 - k, tot = sum[n] - sum[n - k]; i >= 0; i--) {

      if (sum[i + k] - sum[i] >= tot) {

        tot = sum[i + k] - sum[i];

        right[i] = i;

      } else {

        right[i] = right[i + 1];

      }

    }



    // Find the max sum by iterating through the middle interval index based on

    // above 2 cache.

    int maxSum = 0;

    for (int i = k; i <= n - 2 * k; i++) {

      int l = left[i - 1], r = right[i + k];

      int tot = sum[l + k] - sum[l] + sum[r + k] - sum[r] + sum[i + k] - sum[i];

      if (tot > maxSum) {

        ret[0] = l;

        ret[1] = i;

        ret[2] = r;

        maxSum = tot;

      }

    }



    return ret;

  }

https://blog.csdn.net/fuxuemingzhu/article/details/82947707

看题目的数据知道需要用O(N)的解法，另外优化最值问题一般都是DP。具体怎么做呢？

把三个数组分别看做左侧，中间，右侧的数组。我们指定了中间数组的位置之后，就在这个位置左侧和右侧分别求一个和最大的子数组，然后三个数组和相加，就得到了总体最大的和。

使用sums数组保存到每个位置的累积和。这样做的好处是我们可以直接根据两个位置相减求出子数组的和。另外需要两个DP数组left和right。

left[i]表示在区间[0, i]范围内长度为k且和最大的子数组的起始位置

right[i]表示在区间[i, n - 1]范围内长度为k且和最大的子数组的起始位置

left的求法是从左到右遍历，right的求法是从右到左遍历。遍历刚开始的K个位置内由于子数组长度小于k，所以left的值是0，right的值是N - k，代表的是能取子区间的边缘情况下索引。更新过程也不难，就是和已有的子数组最大和比较，然后更新索引位置就行了。

求出了每个位置左边和右边的长度为k的子数组之后，需要再次用一个窗口遍历数组，这个窗口就是我们中间的数组。这就成为了在确定中间数组位置的情况下，左边和右边的最大数组和问题，因为我们已经知道了left和right，那么就相当于查表得到位置。

这个题对sums是添加了头部0的，这样的好处是求到目前为止的和的时候可以直接从nums第0个数组开始找前面一个sums+当前的数字。

https://leetcode.com/articles/maximum-sum-of-3-non-overlapping-intervals/
Approach #1: Ad-Hoc [Accepted]

It is natural to consider an array W of each interval's sum, where each interval is the given length K. To create W, we can either use prefix sums, or manage the sum of the interval as a window slides along the array.

From there, we approach the reduced problem: Given some array W and an integer K, what is the lexicographically smallest tuple of indices (i, j, k) with i + K <= j and j + K <= k that maximizes W[i] + W[j] + W[k]?

Suppose we fixed j. We would like to know on the intervals $i \in [0, j-K]$ and $k \in [j+K, \text{len}(W)-1]$, where the largest value of $W[i]$ (and respectively $W[k]$) occurs first. (Here, first means the smaller index.)

We can solve these problems with dynamic programming. For example, if we know that $i$ is where the largest value of $W[i]$ occurs first on $[0, 5]$, then on $[0, 6]$ the first occurrence of the largest $W[i]$ must be either $i$ or $6$. If say, $6$ is better, then we set best = 6.

At the end, left[z] will be the first occurrence of the largest value of W[i] on the interval $i \in [0, z]$, and right[z] will be the same but on the interval $i \in [z, \text{len}(W) - 1]$. This means that for some choice j, the candidate answer must be (left[j-K], j, right[j+K]). We take the candidate that produces the maximum W[i] + W[j] + W[k].

• Time Complexity: $O(N)$, where $N$ is the length of the array. Every loop is bounded in the number of steps by $N$, and does $O(1)$ work.
• Space complexity: $O(N)$. W, left, and right all take $O(N)$ memory.

  public int[] maxSumOfThreeSubarrays(int[] nums, int K) {

    // W is an array of sums of windows

    int[] W = new int[nums.length - K + 1];

    int sum = 0;

    for (int i = 0; i < nums.length; i++) {

      sum += nums[i];

      if (i >= K)

        sum -= nums[i - K];

      if (i >= K - 1)

        W[i - K + 1] = sum;

    }

    int[] left = new int[W.length];

    int best = 0;

    for (int i = 0; i < W.length; i++) {

      if (W[i] > W[best])

        best = i;

      left[i] = best;

    }

    int[] right = new int[W.length];

    best = W.length - 1;

    for (int i = W.length - 1; i >= 0; i--) {

      if (W[i] >= W[best])

        best = i;

      right[i] = best;

    }

    int[] ans = new int[] { -1, -1, -1 };

    for (int j = K; j < W.length - K; j++) {

      int i = left[j - K], k = right[j + K];

      if (ans[0] == -1 || W[i] + W[j] + W[k] > W[ans[0]] + W[ans[1]] + W[ans[2]]) {

        ans[0] = i;

        ans[1] = j;

        ans[2] = k;

      }

    }

    return ans;

  }

https://zhuhan0.blogspot.com/2017/11/leetcode-689-maximum-sum-of-3-non.html

since the answer is
If there are multiple answers, return the lexicographically smallest one.

https://www.jiuzhang.com/solution/maximum-sum-of-3-non-overlapping-subarrays/

1. 首先预处理前缀和，使sum[i]代表以第i个数结尾的长度为k的子串和，方便我们之后的计算某个区间的和
2. 最朴素的方法是对三段的起始位置进行遍历，求和，时间复杂度是O(n^3)
3. 那么如何优化呢？我们先不考虑下标，只考虑答案最大。如果已知前n个字符中符合题意描述“互相不覆盖的长度为k的子串”的1串最大和为sum_max，那么我们加上当前串的值value，就组成了前n+1个串中符合题意描述的2串最大和，为sum_max+value
4. 因此，对于第i个位置的求和，我们考虑从[0,i-k]的状态转移，在已知的子串和中加入新的子串，求得从起始到i位的两串最大值。同理，如果我们从后往前做相同处理，可以得到从后往前的i位两串最大值
5. 换言之，可以考虑将它划分为三个区域[0,i-k] [i,i+k-1][i+k,len)，我们只需要枚举中间的sum[i]，早预处理从左到当前位置的最大前缀和，从右到当前位置的最大后缀和，加起来就必定是当前位置能找到的最大和，遍历一遍就能取得最终解
6. 参考程序给出的left和right分别记录从左到第i位和从右到第i位的最大sum的下标，因为题意要字典序最小，所以在更新right的时候注意符号
7. Follow up question：如果要求n个而不是三个，应该如何解决?

X. https://leetcode.com/problems/maximum-sum-of-3-non-overlapping-subarrays/discuss/108246/C++-O(n)-time-O(n)-space-concise

Let b[i] be contiguous sum of k elements ending with index i. We need to find the max sum of b[x] + b[y] + b[z] where x + 2k <= y + k <= z. We traverse the array, store solutions for cases of 1 sum (delayed by 2*k steps) , 2 sums (delayed by k steps), 3 sums (no delay) and update those each time we visit new element.

    vector<int> maxSumOfThreeSubarrays(vector<int>& a, int k) {
        int n = a.size();
        vector<int> c[3], m(3); //store optimal solutions for 1 sum, 2 sums, 3 sums.
        vector<int> b(n);
        int sm = 0;
        for (int i = 0; i < n; ++i) {
            sm += a[i];
            if (i >=k-1) {
                b[i] = sm;
                sm -= a[i-k+1];
                if (i >= 3 * k-1) {
                    if (b[i-k-k] > m[0]) { // update 1 sum solution
                        m[0] = b[i-k-k];
                        c[0] = {i-k-k};
                    }
                    if (b[i-k] + m[0] > m[1]) { // update 2 sums solution
                        m[1] = b[i-k] + m[0];
                        c[1] = {c[0][0], i-k};
                    }
                    if (b[i] + m[1] > m[2]) { //update 3 sums solution
                        m[2] = m[1] + b[i];
                        c[2] = {c[1][0], c[1][1], i};
                    }
                }
            }
        }
        
        return {c[2][0]-k + 1,c[2][1]-k+1,c[2][2]-k+1};
    }

X. https://www.hrwhisper.me/leetcode-contest-52-solution/

枚举a~b、b~i、i之后的三段O(n^3)，不用看也知道TLE

如何加速?

为了方便描述，下面将a~b、b~i、i之后三段称为a、b、i

如果我们枚举i，对于当前的这个i，那么我们要是知道a、b两段的和的最大值就好了。

换句话说，假设已知a、b两段的和的最大值，那么我们只需要枚举i即可。

因此我们可以用dp[k][i]来表示前i个数字分为k-1段的最大和。

则显然有dp[k][i] = max(dp[k – 1][i – k] + sum[i -k + 1…i], dp[k][i – 1])

最后回溯恢复下标即可

vector<int> maxSumOfThreeSubarrays(vector<int>& nums, int k) {

if (nums.empty()) return vector<int>{};

vector<int> sum(nums.size(), 0);

sum[0] = nums[0];

for (int i = 1; i < nums.size(); ++i)

sum[i] += nums[i] + sum[i - 1];

vector<vector<int>> dp(3, vector<int>(nums.size(), 0));

dp[0][k - 1] = sum[k - 1];

for (int i = k; i < nums.size(); ++i) {

dp[0][i] = max(sum[i] - sum[i - k], dp[0][i - 1]);

if (i >= k) {

dp[1][i] = max(dp[0][i - k] + sum[i] - sum[i - k], dp[1][i - 1]);

if(i >= 2*k)

dp[2][i] = max(dp[1][i - k] + sum[i] - sum[i - k], dp[2][i - 1]);

}

}

vector<int> ans(3, 0);

ans[2] = max_element(dp[2].begin(), dp[2].end()) - dp[2].begin();

for (int i = 1; i >= 0; --i)

ans[i] = find(dp[i].begin(), dp[i].end(), dp[i + 1][ans[i + 1]] - (sum[ans[i + 1]] - sum[ans[i + 1] - k])) - dp[i].begin();

for (int i = 0; i < 3; ++i)

ans[i] -= k - 1;

return ans;

}

https://leetcode.com/problems/maximum-sum-of-3-non-overlapping-subarrays/discuss/108238/Python-o(n)-time-o(1)-space.-Greedy-solution.

A greedy solution using three sliding windows where you keep track of the best indexes/sums as you go.

O(n) time: Since we're only going through the list once and using no complex operations, this is O(n).
O(1) space: Just a fixed set of temp vars. We don't need the extra arrays that the DP solutions have.

    public int[] maxSumOfThreeSubarrays(int[] nums, int k) {
        // Best single, double, and triple sequence found so far
        int bestSeq = 0;
        int[] bestTwoSeq = {0, k};
        int[] bestThreeSeq = {0, k, k*2};

        // Sums of each window
        int seqSum = 0;
        for (int i = 0; i < k; i++) {
            seqSum += nums[i];
        }
        int seqTwoSum = 0;
        for (int i = k; i < k * 2; i++) {
            seqTwoSum += nums[i];
        }
        int seqThreeSum = 0;
        for (int i = k * 2; i < k * 3; i++) {
            seqThreeSum += nums[i];
        }

        // Sums of combined best windows
        int bestSeqSum = seqSum;
        int bestTwoSum = seqSum + seqTwoSum;
        int bestThreeSum = seqSum + seqTwoSum + seqThreeSum;

        // Current window positions
        int seqIndex = 1;
        int twoSeqIndex = k + 1;
        int threeSeqIndex = k*2 + 1;
        while (threeSeqIndex <= nums.length - k) {
            // Update the three sliding windows
            seqSum = seqSum - nums[seqIndex - 1] + nums[seqIndex + k - 1];
            seqTwoSum = seqTwoSum - nums[twoSeqIndex - 1] + nums[twoSeqIndex + k - 1];
            seqThreeSum = seqThreeSum - nums[threeSeqIndex - 1] + nums[threeSeqIndex + k - 1];
            
            // Update best single window
            if (seqSum > bestSeqSum) {
                bestSeq = seqIndex;
                bestSeqSum = seqSum;
            }

            // Update best two windows
            if (seqTwoSum + bestSeqSum > bestTwoSum) {
                bestTwoSeq[0] = bestSeq;
                bestTwoSeq[1] = twoSeqIndex;
                bestTwoSum = seqTwoSum + bestSeqSum;
            }

            // Update best three windows
            if (seqThreeSum + bestTwoSum > bestThreeSum) {
                bestThreeSeq[0] = bestTwoSeq[0];
                bestThreeSeq[1] = bestTwoSeq[1];
                bestThreeSeq[2] = threeSeqIndex;
                bestThreeSum = seqThreeSum + bestTwoSum;
            }

            // Update the current positions
            seqIndex += 1;
            twoSeqIndex += 1;
            threeSeqIndex += 1;
        }

        return bestThreeSeq;
    }

     maintain m(here m is 3) sliding windows
     */
    public int[] maxSumOfThreeSubarrays(int[] nums, int k) {
        int n = nums.length;
        int m = 3;
        
        // sum[i]: 第i个subarray的和
        // max_sum[i]: 前i个subarrays的和
        int[] sum = new int[m+1];
        int[] max_sum = new int[m+1];
        
        // 对于前i个subarrays，sum达到最大时，它们的index开始位置储存在idx.get(i)中
        List<List<Integer>> idx = new ArrayList<>();
        for (int i = 0; i < m; i++) {
            idx.add(new ArrayList<>());
        }
        
        // 初始化上面的各个array
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j <= i; ++j) {
                idx.get(i).add(j*k);
            }
            int tmp = 0;
            for (int l = k * i; l < (i+1)*k; l++) {
                tmp += nums[l];
            }
            sum[i + 1] = tmp;
            max_sum[i + 1] = max_sum[i] + sum[i + 1]; 
        }
        
        // windows整体往右移动时，从左到右update对于1,2,...m个subarray的最优解（即保证sum为最大）
        for (int i = 1; i <= n - m*k; ++i) {
            for (int j = 0; j < m; ++j) {
                sum[j + 1] += nums[i + (j+1)*k - 1] - nums[i + j*k - 1];
                if (sum[j + 1] + max_sum[j] > max_sum[j + 1]) {
                    max_sum[j + 1] = sum[j + 1] + max_sum[j];
                    idx.get(j).set(j, i + j*k);
                    for (int r = 0; r < j; ++r) {
                        idx.get(j).set(r, idx.get(j-1).get(r));
                    } 
                }
            }
        }
        
        // 最后返回对于m个subarrays最优解的index
        int[] res = new int[idx.get(m-1).size()];
        int cnt = 0;
        for (int i : idx.get(m-1)) res[cnt++] = i;
        
        return res;
    }




X. Follow up
https://www.geeksforgeeks.org/k-maximum-sums-non-overlapping-contiguous-sub-arrays/
Given an Array of Integers and an Integer value k, find out k non-overlapping sub-arrays which have k maximum sums.

Kadane’s algorithm finds out only the maximum subarray sum, but using the same algorithm we can find out k maximum non-overlapping subarray sums. The approach is:

• Find out the maximum subarray in the array using Kadane’s algorithm. Also find out its starting and end indices. Print the sum of this subarray.
• Fill each cell of this subarray by -infinity.
• Repeat process 1 and 2 for k times.

Time Complexity: The outer loop runs for k times and kadane’s algorithm in each iteration runs in linear time O(n). Hence the overall time complexity is O(k*n).

    static void kmax(int arr[], int k, int n) {

      

        // In each iteration it will give

        // the ith maximum subarray sum.

        for(int c = 0; c < k; c++)

        { 

            // Kadane's algorithm.

            int max_so_far = Integer.MIN_VALUE;

            int max_here = 0;

      

            // compute starting and ending

            // index of each of the sub-array.

            int start = 0, end = 0, s = 0;

            for(int i = 0; i < n; i++)

            {

                max_here += arr[i];

                if (max_so_far < max_here)

                {

                    max_so_far = max_here;

                    start = s;

                    end = i;

                }

                if (max_here < 0)

                    {

                    max_here = 0;

                    s = i + 1;

                }

            }

      

            // Print out the result.

            System.out.println("Maximum non-overlapping sub-arraysum" +

                                (c + 1) + ": " +  max_so_far + 

                                ", starting index: " + start +

                                ", ending index: " + end + ".");

      

            // Replace all elements of the maximum subarray 

            // by -infinity. Hence these places cannot form 

            // maximum sum subarray again.

            for (int l = start; l <= end; l++)

                arr[l] = Integer.MIN_VALUE;

        }

        System.out.println();

    }




https://github.com/YaokaiYang-assaultmaster/LeetCode/blob/master/GeneralizedMethod/Maximum%20Sum%20of%20n%20Non-Overlapping%20Subarrays.md

This is a generalized method for 689. Maximum Sum of 3 Non-Overlapping Subarrays .

In this solution, dp[i][j] is used for recording for ith interval, what are the max sums for first j numbers in each position. And index[i][j] is used for recording for ith interval, what are the current start index for first j numbers that made up the max sum.

Thus after the searching ends, dp[n][nums.length] stores the max sum we can get and index[n][nums.length] stores the start index of last interval for the max sum. And now we can search backwards for each previous start index based on the start index of current interval. Because the start index of previous interval is the index stored in index[i - 1][current start index], which is the max sum of the subarray before current start index.

Run time complexity is O(n * len) where n is the number of intervals needed and len is the length of input array.

Space complexity is O(n * len) as well.

  /**

   * @param nums input array of numbers

   * @param k    length of each interval

   * @param n    number of intervals

   * @return start index of each interval that has the maximum sum

   */

  public int[] maxSumOfThreeSubarrays(int[] nums, int k, int n) {

    int[][] dp = new int[n + 1][nums.length + 1];

    int[][] index = new int[n + 1][nums.length + 1];

    int tot = 0;

    // prefix sum

    int[] sum = new int[nums.length + 1];

    for (int i = 0; i < nums.length; i++) {

      sum[i + 1] = nums[i] + sum[i];

    }

    for (int i = 1; i <= n; i++) {

      for (int j = k - 1; j < nums.length; j++) {

        int tmpMax = sum[j + 1] - sum[j - k + 1] + dp[i - 1][j - k + 1];

        if (tmpMax > dp[i][j]) {

          dp[i][j + 1] = tmpMax;

          index[i][j + 1] = j - k + 1;

        } else {

          dp[i][j + 1] = dp[i][j];

          index[i][j + 1] = index[i][j];

        }

      }

    }

    int[] ret = new int[n];

    int prev = nums.length;

    for (int i = n; i > 0; i--) {

      ret[i - 1] = index[i][prev];

      prev = ret[i - 1];

    }

    return ret;

  }

https://leetcode.com/problems/maximum-sum-of-3-non-overlapping-subarrays/discuss/108230/Clean-Java-DP-O(n)-Solution.-Easy-extend-to-Sum-of-K-Non-Overlapping-SubArrays.

This is a more general DP solution, and it is similar to that buy and sell stock problem

dp[i][j] stands for in i th sum, the max non-overlap sum we can have from 0 to j
id[i][j] stands for in i th sum, the first starting index for that sum.

    public int[] maxSumOfThreeSubarrays(int[] nums, int k) {
        int[] ans = new int[3];
        int[][] dp = new int[4][nums.length + 1];
        int[][] pi = new int[4][nums.length + 1];
        for (int i = 0; i <= nums.length; i++) {
            dp[0][i] = 0;
        }
        int[] preSum = new int[nums.length + 1];
        preSum[0] = 0;
        int sum = 0;
        for (int i = 0; i < nums.length; i++) {
            sum += nums[i];
            preSum[i + 1] = sum;
        }
        for (int i = 1; i < 4; i++) {
            for (int j = k; j <= nums.length; j++) { // j: interval end, 1-index based due to sequence dp 
                //do not choose j as one of the intervals end
                if (j > 0) {
                    dp[i][j] = dp[i][j - 1];
                    pi[i][j] = pi[i][j - 1];
                }
                int temp = preSum[j] - preSum[j - k] + dp[i - 1][j - k];
                if (temp > dp[i][j]) {
                    dp[i][j] = temp;
                    pi[i][j] = j - k + 1;// interval starting point, 1-index based
                }
            }
        }
        ans[2] = pi[3][nums.length] - 1;
        ans[1] = pi[2][ans[2]] - 1;//ans[2] 0-index based next interval starting point, last interval end point should be up to ans[2] - 1, change to 1-index based ans[2] - 1 + 1
        ans[0] = pi[1][ans[1]] - 1;
        return ans;
    }




http://juliachencoding.blogspot.com/2018/01/leetcode-689-maximum-sum-of-3-non_23.html

X.https://zhuhan0.blogspot.com/2017/11/leetcode-689-maximum-sum-of-3-non.html

https://www.geeksforgeeks.org/maximum-sum-two-non-overlapping-subarrays-of-given-size/

Given an array, we need to find two subarrays with a specific length K such that sum of these subarrays is maximum among all possible choices of subarrays.

Input : arr[] = [2, 5, 1, 2, 7, 3, 0]
        K = 2
Output : 2 5
         7 3
We can choose two arrays of maximum sum
as [2, 5] and [7, 3], the sum of these two 
subarrays is maximum among all possible 
choices of subarrays of length 2.

Input : arr[] = {10, 1, 3, 15, 30, 40, 4, 50, 2, 1}
        K = 3
Output : 3 15 30 
         40 4 50 

We can solve this problem similar to two pointers method. First we store the prefix sum in a separate array so that any subarray sum can be calculated in constant time. After that we will initialize our two subarray from (N – 2K) and (N – K) indices, where N is the length of the array and K is required subarray length. Then we will move from (N – 2K) index towards 0 and each time we will check whether subarray sum at current index and subarray sum at (current index + K) is greater than previously chosen subarray or not if they are, then update the summation. We can see here that as we need to maximize our sum, we can treat both subarrays independently. At each index we will check subarray sum at current index and subarray sum at K distance away and we will choose maximum sum independently and update the final answer as summation of both these array. In below code index is also taken with sum in form of a pair to actually print the subarrays. Total time complexity of solution will be linear.

// Utility method to get sum of subarray

// from index i to j

int getSubarraySum(int sum[], int i, int j)

{

    if (i == 0)

        return sum[j];

    else

        return (sum[j] - sum[i - 1]);

}

  

// Method prints two non-overlapping subarrays of

// length K whose sum is maximum

void maximumSumTwoNonOverlappingSubarray(int arr[],

                                      int N, int K)

{

    int sum[N];

  

    // filling prefix sum array

    sum[0] = arr[0];

    for (int i = 1; i < N; i++)

        sum[i] = sum[i - 1] + arr[i];

  

    //  initializing subarrays from (N-2K) and (N-K) indices

    pair<int, int> resIndex = make_pair(N - 2 * K, N - K);

  

    //  initializing result sum from above subarray sums

    int maxSum2Subarray = getSubarraySum(sum, N - 2 * K, N - K - 1) +

                          getSubarraySum(sum, N - K, N - 1);

  

    //  storing second subarray maximum and its starting index

    pair<int, int> secondSubarrayMax = make_pair(N - K,

                          getSubarraySum(sum, N - K, N - 1));

  

    //  looping from N-2K-1 towards 0

    for (int i = N - 2 * K - 1; i >= 0; i--)

    {

        //  get subarray sum from (current index + K)

        int cur = getSubarraySum(sum, i + K, i + 2  * K - 1);

  

        // if (current index + K) sum is more  then update

        // secondSubarrayMax

        if (cur >= secondSubarrayMax.second)

            secondSubarrayMax = make_pair(i + K, cur);

  

        //  now getting complete sum (sum of both subarrays)

        cur = getSubarraySum(sum, i, i + K - 1) +

              secondSubarrayMax.second;

  

        //  if it is more then update main result

        if (cur >= maxSum2Subarray)

        {

            maxSum2Subarray = cur;

            resIndex = make_pair(i, secondSubarrayMax.first);

        }

    }

  

    //  printing actual subarrays

    for (int i = resIndex.first; i < resIndex.first + K; i++)

        cout << arr[i] << " ";

    cout << endl;

  

    for (int i = resIndex.second; i < resIndex.second + K; i++)

        cout << arr[i] << " ";

    cout << endl;

}




X. https://www.geeksforgeeks.org/max-sum-of-m-non-overlapping-subarrays-of-size-k/

Given an array and two numbers M and K. We need to find sum of max M subarrays of size K (non-overlapping) in the array. (Order of array remains unchanged). K is the size of subarrays and M is the count of subarray. It may be assumed that size of array is more than m*k. If total array size is not multiple of k, then we can take partial last array.

Examples :

Input: N = 7, M = 3, K = 1 
       arr[] = {2, 10, 7, 18, 5, 33, 0}; 
Output: 61 
Explanation: subsets are: 33, 18, 10 (3 subsets of size 1) 

1. We create a presum array, which contains in each index sum of all elements from ‘index‘ to ‘index + K’ in the given array. And size of the sum array will be n+1-k.
2. Now if we include the subarray of size k, then we can not include any of the elements of that subarray again in any other subarray as it will create overlapping subarrays. So we make recursive call by excluding the k elements of included subarray.
3. if we exclude a subarray then we can use the next k-1 elements of that subarray in other subarrays so we will make recursive call by just excluding the first element of that subarray.
4. At last return the max(included sum, excluded sum)

static void calculatePresumArray(int presum[],

                                 int arr[], 

                                 int n, int k)

{ 

    for (int i = 0; i < k; i++)

    presum[0] += arr[i];

  

    // store sum of array index i to i+k 

    // in presum array at index i of it.

    for (int i = 1; i <= n - k; i++) 

    presum[i] += presum[i - 1] + arr[i + k - 1] - 

                                 arr[i - 1];

}

  

// calculating maximum sum of

// m non overlapping array

static int maxSumMnonOverlappingSubarray(int presum[],

                                         int m, int size, 

                                         int k, int start)

{

    // if m is zero then no need 

    // any array of any size so

    // return 0.

    if (m == 0)

        return 0;

  

    // if start is greater then the 

    // size of presum array return 0.

    if (start > size - 1)

        return 0;

  

    int mx = 0;

  

    // if including subarray of size k

    int includeMax = presum[start] + 

            maxSumMnonOverlappingSubarray(presum,

                      m - 1, size, k, start + k);

  

    // if excluding element and searching 

    // in all next possible subarrays

    int excludeMax = 

            maxSumMnonOverlappingSubarray(presum,

                          m, size, k, start + 1);

  

    // return max

    return Math.max(includeMax, excludeMax);

}

https://www.geeksforgeeks.org/k-maximum-sum-overlapping-contiguous-sub-arrays/

Given an Array of Integers and an Integer value k, find out k sub-arrays(may be overlapping) which have k maximum sums.

Examples:

Input : arr = {4, -8, 9, -4, 1, -8, -1, 6}, k = 4
Output : 9 6 6 5

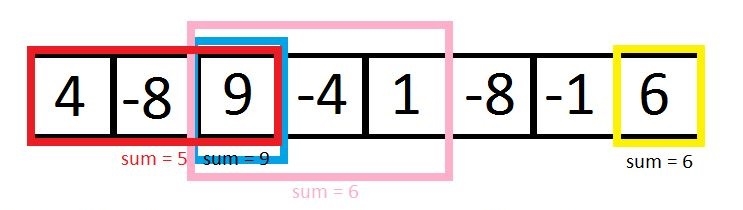
Using Kadane’s Algorithm we can find the maximum contiguous subarray sum of an array. But in the case Kadane’s Algorithm does not work. As whenever we hit an negative number in the array we set the max_ending_here variable to zero, hence we miss the possibilities for second and so on maximums.

Here we is an algorithm presented by Sung Eun Bae and Tadao Takaoka which computes the maximum sub-array sum problem in O(n) time and k maximum sub-array sum problem in O(k*n) time.

First we look at the problem of only maximum sub-array sum using this method:

Prerequisite:
1. Prefix sum array
2. Maximum subarray sum in O(n) using prefix sum

Method for k-maximum sub-arrays:

1. Calculate the prefix sum of the input array.
2. Take cand, maxi and mini as arrays of size k. 
3. Initialize mini[0] = 0 for the same reason as previous.
4. for each value of the prefix_sum[i] do
       (i). update cand[j] value by prefix_sum[i] - mini[j]
       (ii). maxi will be the maximum k elements of maxi and cand
       (iii). if prefix_sum is minimum than all values of mini then 
              include it in mini and remove maximum element form mini
       // After the ith iteration mini holds k minimum prefix sum upto
       // index i and maxi holds k maximum overlapping sub-array sums 
       // upto index i.
5. return maxi 

Throughout this calculation method we keep maxi in non-increasing and mini in non-decreasing order.

Time Complexity: The ‘insertMini’ and ‘maxMerge’ functions runs in O(k) time and it takes O(k) time to update the ‘cand’ array. We do this process for n times. Hence, the overall time complexity is O(k*n).

// Function to compute prefix-sum of the input array

vector<int> prefix_sum(vector<int> arr, int n)

{

    vector<int> pre_sum;

    pre_sum.push_back(arr[0]);

    for (int i = 1; i < n; i++) 

        pre_sum.push_back(pre_sum[i - 1] + arr[i]);    

    return pre_sum;

}

  

// Update maxi by k maximum values from maxi and cand

void maxMerge(vector<int>& maxi, vector<int> cand)

{

    // Here cand and maxi arrays are in non-increasing

    // order beforehand. Now, j is the index of the

    // next cand element and i is the index of next

    // maxi element. Traverse through maxi array.

    // If cand[j] > maxi[i] insert cand[j] at the ith

    // position in the maxi array and remove the minimum

    // element of the maxi array i.e. the last element

    // and increase j by 1 i.e. take the next element

    // from cand.

    int k = maxi.size();

    int j = 0;

    for (int i = 0; i < k; i++) {

        if (cand[j] > maxi[i]) {

            maxi.insert(maxi.begin() + i, cand[j]);

            maxi.erase(maxi.begin() + k);

            j += 1;

        }

    }

}

  

// Insert prefix_sum[i] to mini array if needed

void insertMini(vector<int>& mini, int pre_sum)

{

    // Traverse the mini array from left to right.

    // If prefix_sum[i] is less than any element

    // then insert prefix_sum[i] at that position

    // and delete maximum element of the mini array

    // i.e. the rightmost element from the array.

    int k = mini.size();

    for (int i = 0; i < k; i++) {

        if (pre_sum < mini[i]) {

            mini.insert(mini.begin() + i, pre_sum);

            mini.erase(mini.begin() + k);

            break;

        }

    }

}

  

// Function to compute k maximum overlapping sub-

// array sums

void kMaxOvSubArray(vector<int> arr, int k)

{

    int n = arr.size();

  

    // Compute the prefix sum of the input array.

    vector<int> pre_sum = prefix_sum(arr, n);

  

    // Set all the elements of mini as +infinite

    // except 0th. Set the 0th element as 0.

    vector<int> mini(k, numeric_limits<int>::max());

    mini[0] = 0;

  

    // Set all the elements of maxi as -infinite.

    vector<int> maxi(k, numeric_limits<int>::min());

  

    // Initialize cand array.

    vector<int> cand(k);

  

    // For each element of the prefix_sum array do:

    // compute the cand array.

    // take k maximum values from maxi and cand

    // using maxmerge function.

    // insert prefix_sum[i] to mini array if needed

    // using insertMini function.

    for (int i = 0; i < n; i++) {

        for (int j = 0; j < k; j++) {

             if(pre_sum[i] < 0 && mini[j]==numeric_limits<int>::max())

           cand[j]=(-pre_sum[i])-mini[j];

         else cand[j] = pre_sum[i] - mini[j];

        }

        maxMerge(maxi, cand);

        insertMini(mini, pre_sum[i]);

    }

  

    // Elements of maxi array is the k

    // maximum overlapping sub-array sums.

    // Print out the elements of maxi array.

    for (int ele : maxi)

        cout << ele << " ";

    cout << endl;

}

https://github.com/mintycc/OnlineJudge-Solutions/blob/master/Leetcode/689_Maximum_Sum_of_3_Non_Overlapping_Subarrays.java
1. 分两部分问，先问只有⼀一个subarray求最⼤大和(直接扫⼀一遍array就⾏行行)，
然后是3个subarray和，先让写brute-force，然后再慢慢优化。
2.⽐比如⼀一个数组[1,5,2,-2,3,4], k = 3 它让求两个interval的和的最⼤大值，问
题是，不不是这两个interval分别⻓长k，⽽而是加起来为k……⽐比如k=3就是分成
（1，2）⻓长度的interval（0，3这种不不算）也就是说这道题答案是（5）+
（3+4）= 12
3. follow up, 找三个pairs of numbers that have largest sum, 这三个pairs
互不不重合。ex: [2,1,4,2,1,2,3,5,8] return [4,2], [2,3], [5,8]. 在国⼈人⼤大哥千
⽅方百计提示下才想出了了DP solution， 也不不懂是不不是optimal. ⽅方法是⽤用两
个dp array: dp1[i] 储存i-th element 之前最⼤大的pair 值， dp2[i]储存i-th
element之后最⼤大的pair值。然后再找中间的pair. 假设中间的pair的位置是
j 和 j+1, sum = dp1[j] + dp2[j+1]+array[j] + array[j+1]．