https://www.geeksforgeeks.org/closest-pair-of-points-using-divide-and-conquer-algorithm/
We are given an array of n points in the plane, and the problem is to find out the closest pair of points in the array.
https://www.hackerearth.com/practice/math/geometry/line-sweep-technique/tutorial/
A sweep line is an imaginary vertical line which is swept across the plane rightwards. That's why, the algorithms based on this concept are sometimes also called plane sweep algorithms. We sweep the line based on some events, in order to discretize the sweep.
The events are based on the problem we are considering , we'll see them in the algorithms discussed below. Other than events, we maintain a data structure which stores the events generally sorted by y coordinates (the criteria for ordering of data structure may vary sometimes) which is helpful in the processing when we encounter some event. At any instance, the data structure stores only the active events.
One other thing to note is that the efficiency of this technique depends on the data structures we use. Generally , we can use set in C++ but sometimes we require some extra information to be stored, so we go for balanced binary tree.
For this problem, we can consider the points in the array as our events.
And in a set, we store the already visited points sorted by y coordinate.
So, first we sort the points in x direction as we want our line to move towards right.
Now, suppose we have processed the points from 1 to N-1, and let h be the shortest distance we have got so far. For Nth point, we want to find points whose distance from Nth point is less than or equal to h.
Now, we know we can only go till h distance from to find such point, and in the y direction we can go in h distance upwards and h distance downwards. So, all such points whose x coordinate lie in [] and y coordinates lie in [] are what we are concerned with and these form the active events of the set . All points in the set with x coordinates less than are to be deleted . After this processing, we'll add the Nth point to the set.
One thing to note is that at any instance, the number of points which are active events is O(1)(there can be atmost 5 points around a point which are active excluding the point itself).
Okay, that's a lot of theory, let's see this algo running
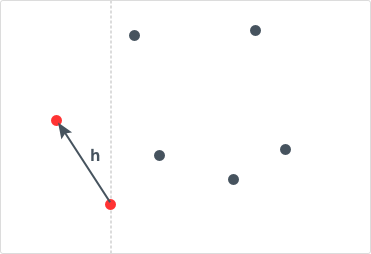

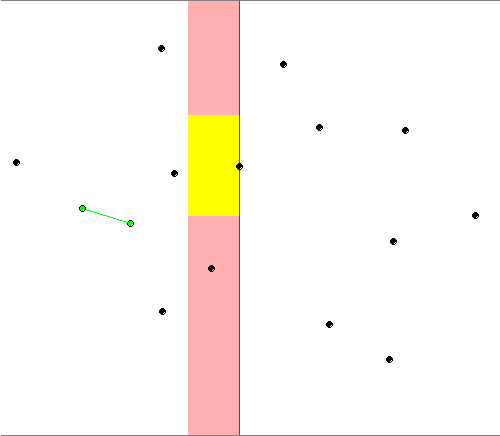
Initialize h as the distance between first two points Update the value of h if present distance between points is less than h
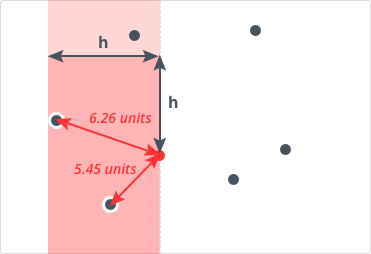
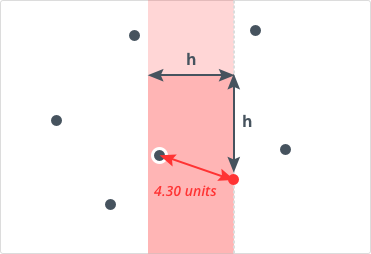
The red region in the image is the region containing points which are to be evaluated with the current point.The points left to this region are removed from the set.
https://www.cs.mcgill.ca/~cs251/ClosestPair/ClosestPairPS.html
X. Divide and Conquer
Following are the detailed steps of a O(n (Logn)^2) algortihm.


https://www.geeksforgeeks.org/closest-pair-of-points-onlogn-implementation/
TODO:
https://en.wikipedia.org/wiki/Closest_pair_of_points_problem
We are given an array of n points in the plane, and the problem is to find out the closest pair of points in the array.
https://www.hackerearth.com/practice/math/geometry/line-sweep-technique/tutorial/
A sweep line is an imaginary vertical line which is swept across the plane rightwards. That's why, the algorithms based on this concept are sometimes also called plane sweep algorithms. We sweep the line based on some events, in order to discretize the sweep.
The events are based on the problem we are considering , we'll see them in the algorithms discussed below. Other than events, we maintain a data structure which stores the events generally sorted by y coordinates (the criteria for ordering of data structure may vary sometimes) which is helpful in the processing when we encounter some event. At any instance, the data structure stores only the active events.
One other thing to note is that the efficiency of this technique depends on the data structures we use. Generally , we can use set in C++ but sometimes we require some extra information to be stored, so we go for balanced binary tree.
For this problem, we can consider the points in the array as our events.
And in a set, we store the already visited points sorted by y coordinate.
So, first we sort the points in x direction as we want our line to move towards right.
Now, suppose we have processed the points from 1 to N-1, and let h be the shortest distance we have got so far. For Nth point, we want to find points whose distance from Nth point is less than or equal to h.
Now, we know we can only go till h distance from to find such point, and in the y direction we can go in h distance upwards and h distance downwards. So, all such points whose x coordinate lie in [] and y coordinates lie in [] are what we are concerned with and these form the active events of the set . All points in the set with x coordinates less than are to be deleted . After this processing, we'll add the Nth point to the set.
One thing to note is that at any instance, the number of points which are active events is O(1)(there can be atmost 5 points around a point which are active excluding the point itself).
Okay, that's a lot of theory, let's see this algo running


Initialize h as the distance between first two points Update the value of h if present distance between points is less than h


The red region in the image is the region containing points which are to be evaluated with the current point.The points left to this region are removed from the set.
Let's break down the points in the code:
1. First ,we have sorted the array of points on x coordinates.
2. Then we inserted the first point in the pnts array to the set box. Note we have defined py as the first in the pair, so set will be sorted by y coordinates.
3. In the loop , for each point in pnts, we are removing the points to the left of the current point whose x coordinate has more distance than h(the current minimum distance) from .This loop runs for overall as we have only N elements in the set. The complexity of erase is . So, the overall complexity of this loop is
4. In the second for loop , we are iterating over all points whose x coordinates lie in [] and y coordinates lie in []. Finding the lower_bound takes and this loop runs for atmost 5 times.
5. For each point, insert into the set. This step takes .
1. First ,we have sorted the array of points on x coordinates.
2. Then we inserted the first point in the pnts array to the set box. Note we have defined py as the first in the pair, so set will be sorted by y coordinates.
3. In the loop , for each point in pnts, we are removing the points to the left of the current point whose x coordinate has more distance than h(the current minimum distance) from .This loop runs for overall as we have only N elements in the set. The complexity of erase is . So, the overall complexity of this loop is
4. In the second for loop , we are iterating over all points whose x coordinates lie in [] and y coordinates lie in []. Finding the lower_bound takes and this loop runs for atmost 5 times.
5. For each point, insert into the set. This step takes .
So, overall time complexity of the algorithm is
#define px second
#define py first
typedef pair<long long, long long> pairll;
pairll pnts [MAX];
int compare(pairll a, pairll b)
{
return a.px<b.px;
}
double closest_pair(pairll pnts[],int n)
{
sort(pnts,pnts+n,compare);
double best=INF;
set<pairll> box;
box.insert(pnts[0]);
int left = 0;
for (int i=1;i<n;++i)
{
while (left<i && pnts[i].px-pnts[left].px > best)
box.erase(pnts[left++]);
for(typeof(box.begin()) it=box.lower_bound(make_pair(pnts[i].py-best, pnts[i].px-best));it!=box.end() && pnts[i].py+best>=it->py;it++)
best = min(best, sqrt(pow(pnts[i].py - it->py, 2.0)+pow(pnts[i].px - it->px, 2.0)));
box.insert(pnts[i]);
}
return best;
}
With that algorithm, we'll sweep the plane from left to right (right to left is also a possibility) and when we reach a point we'll compute all the interesting candidates (the candidates that can be in the closest pair).
For that we'll make the following operations :
- We sort the list of points from left to right in the x axis
- And then for each point :
- We remove from the candidates all the point that are further in x axis that the current min distance
- We take all the candidates that are located more or less current min distance from the current point in y axis
- We test for the min distance all the founded candidates with the current point
- And finally we add the current point to the list of candidates
So when we found a new min distance, we can make the rectangle of candidates smaller in the x axis and smaller in the y axis. So we made a lot less comparisons between the points.
Here is a picture illustrating that :
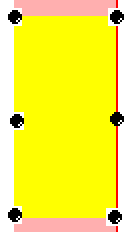
The red points are the closest pair at this time of the algorithm. The red rectangle is the rectangle of the candidates delimited in right by the current point. And the yellow rectangle contains only the candidates interesting for the current point.
There is always a maximum of 6 points in the yellow rectangle, the 4 vertices, the point with the same coordinates as the current point and finally the point in the same y coordinate and in the limit of the x axis. Even if the maximum is 6, you'll almost never have more than 2 points in that list (the maximum is see in my test was 3 with a collection of 1'000'000 random points). You can see this 6 points here :
If all that stuff is not really clear for you, you can watch it in action here in a Java applet.
The candidates must also be always sorted. For that, we'll use a Binary Search Tree for good performances.
If we look at the complexity :
- Sorting all the points in right axis : Cost O(n ln n) with Quick Sort by example
- Shrinking the list of candidates take O(n) from start to end of the algorithm because we add n points to the candidates and we can remove only n points. So this is constant for each point : O(1).
- Searching all the candidates between two values in y axis cost O(ln n) with binary search
- The comparisons with at maximum 6 points are made in O(1)
- Add the candidates and keep the list of candidates sorted cost O(ln n).
So the total complexity is O(n ln(n) + n * ( 1 + ln(n) + 1 + ln(n) ) ) = O(n ln n).
It's really easy to solve. We just have to found the number before which the naive algorithm is quicker than the sweeping and when the size of the points collection is smaller than this pivot number we use the naive implementation. On my computer I found that before 75 elements, the naive implementation was faster than the sweeping algorithm, so we can refactor our method :
public static Point[] closestPair(Point[] points) { if(points.length < 75){ return naiveClosestPair(points); } //No changes }
public static Point[] closestPair(Point[] points) { Point[] closestPair = new Point[2]; //When we start the min distance is the infinity double crtMinDist = Double.POSITIVE_INFINITY; //Get the points and sort them Point[] sorted = Arrays.copyOf(points, points.length); Arrays.sort(sorted, HORIZONTAL_COMPARATOR); //When we start the left most candidate is the first one int leftMostCandidateIndex = 0; //Vertically sorted set of candidates SortedSet<Point> candidates = new TreeSet<Point>(VERTICAL_COMPARATOR); //For each point from left to right for (Point current : sorted) { //Shrink the candidates while (current.x - sorted[leftMostCandidateIndex].x > crtMinDist) { candidates.remove(sorted[leftMostCandidateIndex]); leftMostCandidateIndex++; } //Compute the y head and the y tail of the candidates set Point head = new Point(current.x, (int) (current.y - crtMinDist)); Point tail = new Point(current.x, (int) (current.y + crtMinDist)); //We take only the interesting candidates in the y axis for (Point point : candidates.subSet(head, tail)) { double distance = current.distance(point); //Simple min computation if (distance < crtMinDist) { crtMinDist = distance; closestPair[0] = current; closestPair[1] = point; } } //The current point is now a candidate candidates.add(current); } return closestPair; }
X. Divide and Conquer
Following are the detailed steps of a O(n (Logn)^2) algortihm.
As a pre-processing step, input array is sorted according to x coordinates.
1) Find the middle point in the sorted array, we can take P[n/2] as middle point.
2) Divide the given array in two halves. The first subarray contains points from P[0] to P[n/2]. The second subarray contains points from P[n/2+1] to P[n-1].
3) Recursively find the smallest distances in both subarrays. Let the distances be dl and dr. Find the minimum of dl and dr. Let the minimum be d.

4) From above 3 steps, we have an upper bound d of minimum distance. Now we need to consider the pairs such that one point in pair is from left half and other is from right half. Consider the vertical line passing through passing through P[n/2] and find all points whose x coordinate is closer than d to the middle vertical line. Build an array strip[] of all such points.

5) Sort the array strip[] according to y coordinates. This step is O(nLogn). It can be optimized to O(n) by recursively sorting and merging.
6) Find the smallest distance in strip[]. This is tricky. From first look, it seems to be a O(n^2) step, but it is actually O(n). It can be proved geometrically that for every point in strip, we only need to check at most 7 points after it (note that strip is sorted according to Y coordinate). See this for more analysis.
7) Finally return the minimum of d and distance calculated in above step (step 6)
Time Complexity Let Time complexity of above algorithm be T(n). Let us assume that we use a O(nLogn) sorting algorithm. The above algorithm divides all points in two sets and recursively calls for two sets. After dividing, it finds the strip in O(n) time, sorts the strip in O(nLogn) time and finally finds the closest points in strip in O(n) time. So T(n) can expressed as follows
T(n) = 2T(n/2) + O(n) + O(nLogn) + O(n)
T(n) = 2T(n/2) + O(nLogn)
T(n) = T(n x Logn x Logn)
T(n) = 2T(n/2) + O(n) + O(nLogn) + O(n)
T(n) = 2T(n/2) + O(nLogn)
T(n) = T(n x Logn x Logn)
The great thing about the above approach is, if the array strip[] is sorted according to y coordinate, then we can find the smallest distance in strip[] in O(n) time. In the implementation discussed in previous post, strip[] was explicitly sorted in every recursive call that made the time complexity O(n (Logn)^2), assuming that the sorting step takes O(nLogn) time.
The great thing about the above approach is, if the array strip[] is sorted according to y coordinate, then we can find the smallest distance in strip[] in O(n) time. In the implementation discussed in previous post, strip[] was explicitly sorted in every recursive call that made the time complexity O(n (Logn)^2), assuming that the sorting step takes O(nLogn) time.
In this post, we discuss an implementation where the time complexity is O(nLogn). The idea is to presort all points according to y coordinates. Let the sorted array be Py[]. When we make recursive calls, we need to divide points of Py[] also according to the vertical line. We can do that by simply processing every point and comparing its x coordinate with x coordinate of middle line.
In this post, we discuss an implementation where the time complexity is O(nLogn). The idea is to presort all points according to y coordinates. Let the sorted array be Py[]. When we make recursive calls, we need to divide points of Py[] also according to the vertical line. We can do that by simply processing every point and comparing its x coordinate with x coordinate of middle line.
T(n) = 2T(n/2) + O(n) + O(n) + O(n)
T(n) = 2T(n/2) + O(n)
T(n) = T(nLogn)
T(n) = 2T(n/2) + O(n)
T(n) = T(nLogn)
public ClosestPair(Point2D[] points) {
if (points == null) throw new IllegalArgumentException("constructor argument is null");
for (int i = 0; i < points.length; i++) {
if (points[i] == null) throw new IllegalArgumentException("array element " + i + " is null");
}
int n = points.length;
if (n <= 1) return;
// sort by x-coordinate (breaking ties by y-coordinate)
Point2D[] pointsByX = new Point2D[n];
for (int i = 0; i < n; i++)
pointsByX[i] = points[i];
Arrays.sort(pointsByX, Point2D.X_ORDER);
// check for coincident points
for (int i = 0; i < n-1; i++) {
if (pointsByX[i].equals(pointsByX[i+1])) {
bestDistance = 0.0;
best1 = pointsByX[i];
best2 = pointsByX[i+1];
return;
}
}
// sort by y-coordinate (but not yet sorted)
Point2D[] pointsByY = new Point2D[n];
for (int i = 0; i < n; i++)
pointsByY[i] = pointsByX[i];
// auxiliary array
Point2D[] aux = new Point2D[n];
closest(pointsByX, pointsByY, aux, 0, n-1);
}
// find closest pair of points in pointsByX[lo..hi]
// precondition: pointsByX[lo..hi] and pointsByY[lo..hi] are the same sequence of points
// precondition: pointsByX[lo..hi] sorted by x-coordinate
// postcondition: pointsByY[lo..hi] sorted by y-coordinate
private double closest(Point2D[] pointsByX, Point2D[] pointsByY, Point2D[] aux, int lo, int hi) {
if (hi <= lo) return Double.POSITIVE_INFINITY;
int mid = lo + (hi - lo) / 2;
Point2D median = pointsByX[mid];
// compute closest pair with both endpoints in left subarray or both in right subarray
double delta1 = closest(pointsByX, pointsByY, aux, lo, mid);
double delta2 = closest(pointsByX, pointsByY, aux, mid+1, hi);
double delta = Math.min(delta1, delta2);
// merge back so that pointsByY[lo..hi] are sorted by y-coordinate
merge(pointsByY, aux, lo, mid, hi);
// aux[0..m-1] = sequence of points closer than delta, sorted by y-coordinate
int m = 0;
for (int i = lo; i <= hi; i++) {
if (Math.abs(pointsByY[i].x() - median.x()) < delta)
aux[m++] = pointsByY[i];
}
// compare each point to its neighbors with y-coordinate closer than delta
for (int i = 0; i < m; i++) {
// a geometric packing argument shows that this loop iterates at most 7 times
for (int j = i+1; (j < m) && (aux[j].y() - aux[i].y() < delta); j++) {
double distance = aux[i].distanceTo(aux[j]);
if (distance < delta) {
delta = distance;
if (distance < bestDistance) {
bestDistance = delta;
best1 = aux[i];
best2 = aux[j];
// StdOut.println("better distance = " + delta + " from " + best1 + " to " + best2);
}
}
}
}
return delta;
}
// stably merge a[lo .. mid] with a[mid+1 ..hi] using aux[lo .. hi]
// precondition: a[lo .. mid] and a[mid+1 .. hi] are sorted subarrays
private static void merge(Comparable[] a, Comparable[] aux, int lo, int mid, int hi) {
// copy to aux[]
for (int k = lo; k <= hi; k++) {
aux[k] = a[k];
}
// merge back to a[]
int i = lo, j = mid+1;
for (int k = lo; k <= hi; k++) {
if (i > mid) a[k] = aux[j++];
else if (j > hi) a[k] = aux[i++];
else if (less(aux[j], aux[i])) a[k] = aux[j++];
else a[k] = aux[i++];
}
}
https://en.wikipedia.org/wiki/Closest_pair_of_points_problem
The dynamic version for the closest-pair problem is stated as follows:
- Given a dynamic set of objects, find algorithms and data structures for efficient recalculation of the closest pair of objects each time the objects are inserted or deleted.
If the bounding box for all points is known in advance and the constant-time floor function is available, then the expected O(n) space data structure was suggested that supports expected-time O(log n) insertions and deletions and constant query time. When modified for the algebraic decision tree model, insertions and deletions would require O(log2 n) expected time.[7] It is worth noting, though, that the complexity of the dynamic closest pair algorithm cited above is exponential in the dimension d, and therefore such an algorithm becomes less suitable for high-dimensional problems.
An algorithm for the dynamic closet-pair problem in d dimensional space was developed by Sergey Bespamyatnikh in 1998 [8]. Points can be inserted and deleted in O(logn) time per point (in the worst case).