https://www.codetd.com/article/2798845
经过几个月辛勤的工作,FJ决定让奶牛放假。假期可以在1…N天内任意选择一段(需要连续),每一天都有一个享受指数W。但是奶牛的要求非常苛刻,假期不能短于P天,否则奶牛不能得到足够的休息;假期也不能超过Q天,否则奶牛会玩的腻烦。FJ想知道奶牛们能获得的最大享受指数。
Input
第一行:N,P,Q.
第二行:N个数字,中间用一个空格隔开,每个数都在longint范围内。
第二行:N个数字,中间用一个空格隔开,每个数都在longint范围内。
Output
一个整数,奶牛们能获得的最大享受指数。
Sample Input
5 2 4
-9 -4 -3 8 -6
-9 -4 -3 8 -6
Sample Output
5
Data Constraint
50% 1≤N≤10000
100% 1≤N≤100000
1<=p<=q<=n
Hint
选择第3-4天,享受指数为-3+8=5。
100% 1≤N≤100000
1<=p<=q<=n
Hint
选择第3-4天,享受指数为-3+8=5。
看到区间的问题首先肯定是想到求前缀和,我们把[1,k]的和记为sum[k],可以得到sum[i] = sum[i - 1] + a[i],[l,r]的和即为sum[r] - sum[l - 1](这里视sum[0] = 0)。我们假设选择的区间为[l,r]且r固定,可知r−q+1≤l≤r−p+1r−q+1≤l≤r−p+1,若要使[l,r]区间的值最大,则sum[l - 1]需最小,才可使得sum[r] - sum[l - 1]最小,当i右移一位到i+1,因为p,q为给定不变的值,对应寻找最小sum[l-1]的区间也右移一位,与上题同。
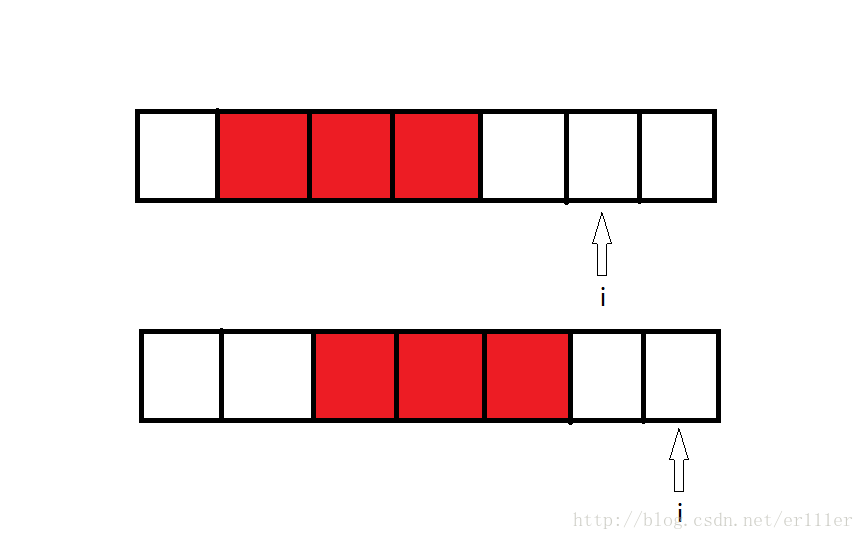
如下图,当p=3,q=5时:
如下图,当p=3,q=5时:

关于单调队列的运用还有很多,例如斜率优化DP等等。总而言之,使用单调队列优化DP,那么必会有求i之前某个范围的极值的操作,这类DP的方程通常为:
F[i]=min(F[j]+a[i]:j<i)F[i]=min(F[j]+a[i]:j<i)
a[i]是与j无关的数。
F[i]=min(F[j]+a[i]:j<i)F[i]=min(F[j]+a[i]:j<i)
a[i]是与j无关的数。
int n,p,q,l,r,head = 1,tail = 0,ans = -2147483647;
int que[100001],a[100001];
long long sum[100001];
int max(long long a,long long b)
{
return a > b ? a : b;
}
int main()
{
sum[0] = 0;
scanf("%d %d %d", &n, &p, &q);
for (int i = 1;i <= n;i++)
{
scanf("%d", &a[i]);
sum[i] = sum[i-1] + a[i]; //记前缀和
}
for (r = p;r <= n;r++)
{
while (head <= tail && sum[que[tail]-1] >= sum[r-p]) tail--; //更优的sum[l - 1]予以插队
que[++tail] = r+1-p; //入队
while (head <= tail && que[head] < r+1-q) head++; //不处于维护范围内的出队
ans = max(ans, sum[r]-sum[que[head]-1]); //更新答案
}
printf("%d\n", ans);
return 0;
}
前缀和 + dp + 单调队列。
写了树状数组。。。。但是树状数组求区间和比前缀和要慢啊。。。
首先前缀和,sum[i] = sum[i - 1] + sum[i – 2];所以对于区间[i,j],区间和sum(i,j) = sum[j] – sum[i],其中j – q <= i <= j – p;这时可以发现,若要sum(i,j)尽量大,那么=sum[i]要尽量小,这时要用单调递增队列维护i的区间,队列中存sum数组的下标。
单调队列满足两个性质:
1.单调队列必须满足从队头到队尾的严格单调性。
2.排在队列前面的比排在队列后面的要先进队。
元素进队列的过程对于单调递增队列,对于一个元素a 如果 a > 队尾元素,那么直接将a扔进队列;如果 a <= 队尾元素 则将队尾元素出队列,直到满足 a 大于队尾元素即可。
枚举j从p到n,即枚举右端点,对于每个枚举的右端点,更新单调队列,首先要保证head始终<= tail,当队尾元素的值sum[que[tail]] > 当前要进队的元素的值sum[j – p]时,队尾的标记tail要前移,tail--;之后队尾元素更新为j – p;对于队首,要保证q[head] > j – q,所以head要++,直到满足。这样更新完成后,队首元素的值就是最小的了,此时在ans与sum[j] – sum[q[head]]间取max。
动态规划,先求一个前缀和sum,ans=max(ans,sum[i]-sum[k])(i-p<=k<=i-q)
根据上式,若ans最大,则sum[k]尽量小,所以单调队列维护区间i-q~i-p的最小值即可。
根据上式,若ans最大,则sum[k]尽量小,所以单调队列维护区间i-q~i-p的最小值即可。
lon n,P,Q,ans=inf,tmp,sum[maxn];
lon head=1,tail,q[maxn];
int main()
{
cin>>n>>P>>Q;
for(int i=1;i<=n;i++)
{
cin>>tmp;
sum[i]=sum[i-1]+tmp;
}
for(int i=P;i<=n;i++)
{
while(head<=tail&&sum[i-P]<sum[q[tail]])
tail--;
q[++tail]=i-P;
while(head<=tail&&q[head]<i-Q)
head++;
ans=max(ans,sum[i]-sum[q[head]]);
}
cout<<ans;
return 0;
}
单调队列 - 有限制的最大和问题
scanf("%d%d%d",&n,&p,&q);
for(int i=1; i<=n; i++)
{
scanf("%lld",&num[i]);
num[i]+=num[i-1];
}
int ans=0x80000000;
std::deque<int> deq; //单调队列
//保存假期的起始点
//单调队列往往保存的是下标
for(int i=p; i<=n; i++)
{
//单调队列第一步:删去非最优解
//这一步最重要
//对于本题而言,如果把之前的数作为起始点还不如把当前点作为起始点,那就删了它
//如果前几个数的和比i-p对应的数还要大,说明num[j]-num[i-p]比num[j]-num[前几个数]要大
while(!deq.empty() && num[deq.back()] > num[i-p])
deq.pop_back();
//单调队列第二步:保存当前解
deq.push_back(i-p); //保存起始位置
//单调队列第三步:删去过时解
//这一步可以放在任何位置,但必须放在更新答案前
while(!deq.empty() && deq.front() < i-q)
deq.pop_front();
//单调队列第四步:更新答案
//答案读取的是front,因为根据之前的操作front是最优解
ans=std::max(ans,int(num[i]-num[deq.front()]));
}
printf("%d",ans);
int main()
{
scanf("%lld %lld %lld", &n, &p, &Q);
rep(i,1,n) scanf("%lld", &a),sum[i] = a + sum[i-1];
rep(i,p,n)
{
while(sum[q[tail]] >= sum[i-p] && head <= tail) tail--;//因为i-p处的元素必须入队,所以队中一切比sum[i-p]大的元素必须出队
q[++tail] = i - p;//把sum[i-p]压入队列
while(q[head] < i - Q) head++;//因为我们最多只能取到i-q这么长的区间,所以在这个区间之前的所有元素必须出列。
f[i] = sum[i] - sum[q[head]];
ans = max(ans, f[i]);
}
printf("%lld\n", ans);
return 0;
}
X.
1.线段树 复杂度(nlogn)
2.单调队列 复杂度(n)
具体实现
1.线段树:
首先预处理出来sum前缀和,
对于每一点i,我们只需要找到符合题意范围内最小的即可
并放入线段树中
对去查询每一个点,用线段树去查询i-q+1~i-p+1之间的最小值
然后去更新最大值
2.单调队列:
构造一个单调队列
当枚举到i的时候,用sum[i-p+1]去更新队列
首先,我们想一想怎么算每个“几天内”的最大值,首先想可以暴力,枚举一次天数,再枚举一次i,时间是 O(n2),爆了。
所以我们还要想一想。
前缀和?可以优化……
线段树?能考虑……
这几个小想法组合起来就可以了,但是好像不是很好想。
我们可以枚举第一个休息日的编号i,我们要算从这个第i天开始,往后的P到Q天里快乐指数最大那一天快乐指数是多少,枚举过后取个max就行了。
按这种方式算的话,如何将时间复杂度优化到最小?
考虑前缀和和线段树。
前缀和数组pre维护的是的快乐指数之和,线段树求的是i+P-1 ~ i+Q-1这一段区间的快乐指数前缀和最大值maxn,我们发现maxn-pre[i]就是从这个第i天开始,往后的P到Q天里快乐指数最大那一天快乐指数是多少。
其实求最大值的部分,用st表或者其他的也行,只不过我觉得线段树更好。
总共的复杂度就是O(nlogn)
所以我们还要想一想。
前缀和?可以优化……
线段树?能考虑……
这几个小想法组合起来就可以了,但是好像不是很好想。
我们可以枚举第一个休息日的编号i,我们要算从这个第i天开始,往后的P到Q天里快乐指数最大那一天快乐指数是多少,枚举过后取个max就行了。
按这种方式算的话,如何将时间复杂度优化到最小?
考虑前缀和和线段树。
前缀和数组pre维护的是的快乐指数之和,线段树求的是i+P-1 ~ i+Q-1这一段区间的快乐指数前缀和最大值maxn,我们发现maxn-pre[i]就是从这个第i天开始,往后的P到Q天里快乐指数最大那一天快乐指数是多少。
其实求最大值的部分,用st表或者其他的也行,只不过我觉得线段树更好。
总共的复杂度就是O(nlogn)