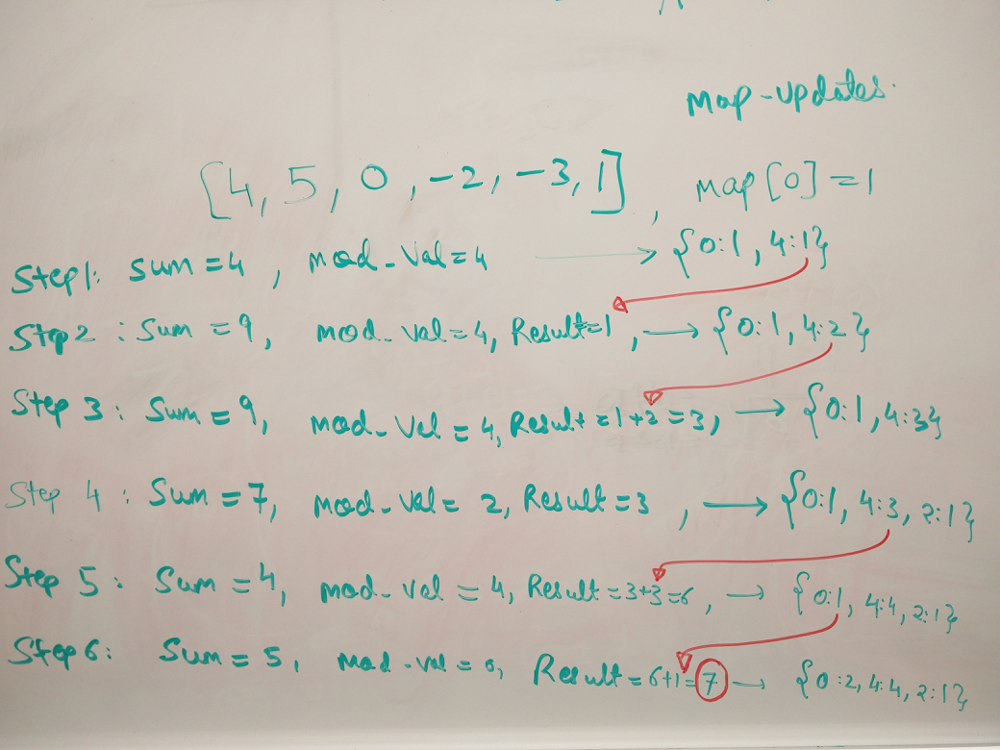Massive Algorithms: LeetCode 974 - Subarray Sums Divisible by K

LeetCode 974 - Subarray Sums Divisible by K

https://leetcode.com/problems/subarray-sums-divisible-by-k/

Given an array A of integers, return the number of (contiguous, non-empty) subarrays that have a sum divisible by K.

Example 1:

Input: A = [4,5,0,-2,-3,1], K = 5
Output: 7
Explanation: There are 7 subarrays with a sum divisible by K = 5:
[4, 5, 0, -2, -3, 1], [5], [5, 0], [5, 0, -2, -3], [0], [0, -2, -3], [-2, -3]

Note:

1 <= A.length <= 30000
-10000 <= A[i] <= 10000
2 <= K <= 10000

Approach 1: Prefix Sums and Counting

As is typical with problems involving subarrays, we use prefix sums to add each subarray. Let P[i+1] = A[0] + A[1] + ... + A[i]. Then, each subarray can be written as P[j] - P[i] (for j > i). Thus, we have P[j] - P[i] equal to 0 modulo K, or equivalently P[i] and P[j] are the same value modulo K.

Algorithm

Count all the P[i]'s modulo K. Let's say there are

C_x

values

P[i] \equiv x \pmod{K}

. Then, there are

\sum_x \binom{C_x}{2}

possible subarrays.

For example, take A = [4,5,0,-2,-3,1]. Then P = [0,4,9,9,7,4,5], and

C_0 = 2, C_2 = 1, C_4 = 4

With $C_0 = 2$ (at $P[0]$ , $P[6]$ ), it indicates $\binom{2}{2} = 1$ subarray with sum divisible by $K$ , namely $A[0:6] = [4, 5, 0, -2, -3, 1]$ .
With $C_4 = 4$ (at $P[1]$ , $P[2]$ , $P[3]$ , $P[5]$ ), it indicates $\binom{4}{2} = 6$ subarrays with sum divisible by $K$ , namely $A[1:2]$ , $A[1:3]$ , $A[1:5]$ , $A[2:3]$ , $A[2:5]$ , $A[3:5]$ .

Time Complexity: $O(N)$ , where $N$ is the length of A.
Space Complexity: $O(N)$ . (However, the solution can be modified to use $O(K)$ space by storing only count.)

public int subarraysDivByK(int[] A, int K) {

int N = A.length;

int[] P = new int[N + 1];

for (int i = 0; i < N; ++i)

P[i + 1] = P[i] + A[i];

int[] count = new int[K];

for (int x : P)

count[(x % K + K) % K]++;

int ans = 0;

for (int v : count)

ans += v * (v - 1) / 2;

return ans;

}

https://www.geeksforgeeks.org/count-sub-arrays-sum-divisible-k/

    static int subCount(int arr[], int n, int k) 

{

        // create auxiliary hash array to 

        // count frequency of remainders 

        int mod[] = new int[k]; 

        Arrays.fill(mod, 0); 

        // Traverse original array and compute cumulative 

        // sum take remainder of this current cumulative 

        // sum and increase count by 1 for this remainder 

        // in mod[] array 

        int cumSum = 0; 

        for (int i = 0; i < n; i++) { 

            cumSum += arr[i]; 

            // as the sum can be negative, taking modulo twice 

            mod[((cumSum % k) + k) % k]++; 

}

        // Initialize result 

        int result = 0; 

        // Traverse mod[] 

        for (int i = 0; i < k; i++) 

            // If there are more than one prefix subarrays 

            // with a particular mod value. 

            if (mod[i] > 1) 

                result += (mod[i] * (mod[i] - 1)) / 2; 

        // add the elements which are divisible by k itself 

        // i.e., the elements whose sum = 0 

        result += mod[0]; 

        return result; 

}

https://www.jianshu.com/p/7d9479ffcd5a

其实上面的解法已经很接近了，但是思考一下为什么会超时？比如K=5，当sum[0]=4时，后面的sum[i]=5*n + 4都符合要求，即不需要判断每个和，只需要判断sum[i]%5的值就好了。
假设：

sum[i]=p*K+ri
sum[j]=q*K+rj

则：

sum[j]-sum[i]=(q-p)*K+rj-ri

若想sum[j]-sum[i]被K整除，只需要rj-ri能够被K整除即可，因为rj和ri都是对K的模，所以只要rj=ri即可。
所以这道题就变成了求对K的每个模的个数，然后对于每个0~i，分别两两组合，假设mod[i]=n，那么其i的个数为n*(n-1)/2.
时间复杂度：O(n)
空间复杂度：O(K)

public int subarraysDivByK(int[] A, int K) {
    int mod[] = new int[K];

    int cumSum = 0;
    for (int i = 0; i < A.length; i++) {
        cumSum += A[i];
        // countSum % K 可能是负数，需要 +K
        mod[((cumSum % K) + K) % K]++;
    }

    int ans = 0;
    for (int i = 0; i < K; i++) {
        if (mod[i] > 1) {
            ans += (mod[i] * (mod[i] - 1)) / 2;
        }
    }

    ans += mod[0];
    return ans;
}

https://blog.csdn.net/dong_beijing/article/details/86444647
大致思路：比如数组A = [1,2,1], K=2，那么1%2 =1，（1+2）%2=1，所以 {2}是符合条件的子数组，而{1}和{1，2}的特点是有共同的余数1。类似的{}和{1，2，1}有共同的余数0，所以{1，2，1}是满足条件的数组。

详细思路：

（1）统计0到A.size()累计和的余数；

（2）统计相同余数的数量；

（3）相同余数的数量累加；

补充，由于题目A为整数，那么要处理负数的情况，负数的余数是A[i]%K+K。

int subarraysDivByK(vector<int>& a, int k) {
int as =a.size();
vector<int> remain(as+1,0);
int sum=0;
for(int i=0;i<as;i++)
{
sum+=a[i];//statistac for remainer
remain[i]=(sum%k+k)%k;//+k for neg
}
vector<int> stat(k,0);
int ret=0;
for(int i=0;i<=as;i++)
{
ret+=stat[remain[i]];//get same remainer counts
stat[remain[i]]++;
}
return ret;
}
X. https://leetcode.com/problems/subarray-sums-divisible-by-k/discuss/217985/JavaC%2B%2B-Count-the-Remainder

Calculate the prefix sum and count it.

Java, use HashMap

    public int subarraysDivByK(int[] A, int K) {
        Map<Integer, Integer> count = new HashMap<>();
        count.put(0, 1);
        int prefix = 0, res = 0;
        for (int a : A) {
            prefix = (prefix + a % K + K) % K;
            res += count.getOrDefault(prefix, 0);
            count.put(prefix, count.getOrDefault(prefix, 0) + 1);
        }
        return res;
    }

Java, Use Array

    public int subarraysDivByK(int[] A, int K) {
        int[] count = new int[K];
        count[0] = 1;
        int prefix = 0, res = 0;
        for (int a : A) {
            prefix = (prefix + a % K + K) % K;
            res += count[prefix]++;
        }
        return res;
    }

https://leetcode.com/problems/subarray-sums-divisible-by-k/discuss/217980/Java-O(N)-with-HashMap-and-prefix-Sum

About the problems - sum of contiguous subarray , prefix sum is a common technique.
Another thing is if sum[0, i] % K == sum[0, j] % K, sum[i + 1, j] is divisible by by K.
So for current index j, we need to find out how many index i (i < j) exit that has the same mod of K.
Now it easy to come up with HashMap <mod, frequency>

Time Complexity: O(N)
Space Complexity: O(K)

Very clever solution with map.put(0,1) to deal with "remainder = 0" situation

    public int subarraysDivByK(int[] A, int K) {
        Map<Integer, Integer> map = new HashMap<>();
        map.put(0, 1);//\\
        int count = 0, sum = 0;
        for(int a : A) {
            sum = (sum + a) % K;
            if(sum < 0) sum += K;  // Because -1 % 5 = -1, but we need the positive mod 4
            count += map.getOrDefault(sum, 0);
            map.put(sum, map.getOrDefault(sum, 0) + 1);
        }
        return count;
    }


we can just use array, which is faster than HashMap.


    public int subarraysDivByK(int[] A, int K) {
        int[] map = new int[K];
  map[0] = 1;
        int count = 0, sum = 0;
        for(int a : A) {
            sum = (sum + a) % K;
            if(sum < 0) sum += K;  // Because -1 % 5 = -1, but we need the positive mod 4
            count += map[sum];
            map[sum]++;
        }
        return count;
    }

https://leetcode.com/problems/subarray-sums-divisible-by-k/discuss/217962/Java-Clean-O(n)-Number-Theory-%2B-Prefix-Sums

I am already going to assume that you know about prefix sums before you read this.
We can all agree that for an array int[] A, where N = len(A), that there are N prefix sums.
prefix[0] = A[0], prefix[1] = A[0] + A[1], ... prefix[i] = prefix[0] + ... + prefix[i].

Then to calculate how many subarrays are divisible by K is logically equivalent to saying, how many ways can we pair up all prefix sum pairs (i,j) where i < j
such that (prefix[j] - prefix[i]) % K == 0.

Just from that information alone we easily get a O(n^2) solution.
Compute all prefix sums, then check all pair to see if k divides the difference between them.

However, if we just exploit some information w.r.t to the remainder of each prefix sum we can manipulate this into a linear algorithm. Here's how.

Number Theory Part
I noted above that we need to find all prefix sum pairs (i,j) such tha (p[j] - p[i]) % K == 0.
But this is only true, if and only if p[j] % K == p[i] % K
Why is this?

According the the division algorithm we can express p[j] and p[i] in the following way.
p[j] = bK + r0 where 0 <= r0 < K
p[i] = aK + r1 where 0<= r1 < K

Then p[j] - p[i] = (b*K + r0) - (a*K + r1)
= b*K - a*K + r0 - r1 = K*(b-a) + r0 - r1
Again: p[j] - p[i] = K*(b-a) + (r0-r1), in other words
K only divides p[j] - p[i] iff r0-r1 = 0 <-> r0 = r1 QED

But we should not forget about elements in the array that do not need a pairing, namely those that are are divisible by K. That's why I add mod[0] at the end.

Also counting pairs => N choose 2 = > n*(n-1) / 2.

https://leetcode.com/problems/subarray-sums-divisible-by-k/discuss/217979/Pictured-Explanation-Python-O(n)-Clean-Solution-8-Lines!

Running Sum[i]%K == Running Sum[j]%k that means we have sum(i,j) which is divisible by K.
Thus, we keep HashMap = {RunningSum%K : Frequency_Count}
Time Complexity : O(n)
Space Complexity : O(K) - As map keys are always Modulus of K with running sum.

X. https://blog.csdn.net/fuxuemingzhu/article/details/86438244
定义DP数组，其中dp[i]代表以i结尾的能被K整除的子数组的最多个数。既然要求子数组的和，那么我们知道，肯定需要求数组累积和sums的。那么，对于sums每个位置i向前找，找到第一个差能被K整除的位置j，就停止即可。此时的dp[i] = dp[j] + 1. 题目要求的结果是sum(dp).

下面分析这个递推公式怎么来的。dp[j]表示以j位置结尾的子数组，该子数组的和能被K整除。那么当我们寻找到(sums[i] - sums[j]) % K == 0的时候，说明子数组sums[i, j]也能被K整除，那么，以i结尾的所有子数组个数等于以j结尾的子数组后面拼接上[i,j]子数组，加上[i,j]子数组.即dp[i] = dp[j] + 1。那么，为什么会break掉呢？这是因为，我们dp的状态是以i结尾的子数组的最大个数，再往前搜索则不是最大的。

这个代码的时间复杂度是O(N^2)的，也AC了，我认为主要是break的功劳。
int subarraysDivByK(vector<int>& A, int K) {
const int N = A.size();
vector<int> sums = {0};
for (int a : A)
sums.push_back(a + sums.back());
vector<int> dp(N + 1, 0);
int res = 0;
for (int i = 1; i <= N; ++i) {
for (int j = i - 1; j >= 0; --j) {
if ((sums[i] - sums[j]) % K == 0) {
dp[i] = dp[j] + 1;
res += dp[i];
break;
}
}
}
return res;
}
前缀和求余
其实，在上面这个做法当中，我们对于每个i位置都向前去查询(sums[i] - sums[j]) % K == 0的j，找到之后立马break，这一步可以更加简化，只要我们使用前缀和，并且相同余数的和。

如果(sums[i] - sums[j]) % K == 0，说明sums[i]和sums[j]都是K的倍数，所以得出sums[i] % K == sums[j] % K。也就是说，我们找到sums[i] % K这个数字的之前的状态即可。根据上面的DP，我们知道只需要找到最后的这个结果，然后break掉的意思就是，我们只需要保存最后的状态。总之，我们需要维护一个hash_map，保存每个余数在每个位置前面，出现的次数。

刚开始时，m[0] = 1，即假设0的出现了1次。然后遍历每个数字，对前缀和+当前数字再求余，在C++里面由于负数求余得到的是负数，所以要把负余数+K才行。把字典中保存的之前的结果累计，就是结果。

想了很久为什么是加的当前数字之前的结果，而不是现在的结果？这是因为，我们当前再次遇到了这个数字，才能说明形成了一个同余的区间。所以加的永远是前面的余数存在了多少次。这样，当某个余数只出现了1次时，并不会计入到结果里。
int subarraysDivByK(vector<int>& A, int K) {
unordered_map<int, int> m;
int preSum = 0;
int res = 0;
m[0] = 1;
for (int a : A) {
preSum = (preSum + a) % K;
if (preSum < 0) preSum += K;
res += m[preSum]++;
}
return res;
}

LeetCode 974 - Subarray Sums Divisible by K

Labels

Popular Posts