https://threads-iiith.quora.com/Tutorial-on-Trie-and-example-problems
https://www.hackerrank.com/challenges/xor-key/topics


 All leaf nodes have winning strategy.
All leaf nodes have winning strategy.
https://www.hackerrank.com/challenges/xor-key/topics
But we will be dealing with numbers here, and particularly in binary bits. We'll see as we solve problems.
Problem1: Given an array of integers, we have to find two elements whose XOR is maximum. Solution: Suppose we have a data structure in which can satisfy two types of queries:
- Insert a number X.
- Given a Y, find maximum XOR of Y with all numbers that have been inserted till now.
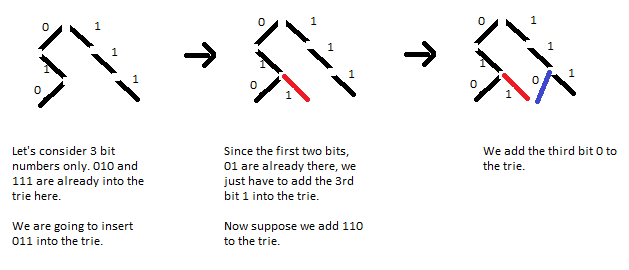
If we have this data structure, we'll insert integers as we go, and with query of type we'll find the maximum XOR. Trie is the data structure we'll use. First, let's see how we insert elements in the trie.

So, we trace the path of the number we have to insert, we don't have to draw the existing path again.
Insertion of an N length key takes O(N) which is log2(MAX) where MAX is the maximum number to be inserted in trie, because there are at maximum log2(MAX) binary bits in a number. This way we store all the data about all the numbers inserted into trie till now. Now, for query of type 2: Let's say our number Y is b1,b2...bn, where b1,b2.. are binary bits. We start from b1. Now for the XOR to be maximum, we'll try to make most significant bit 1 after taking XOR. So, if b1 is 0, we'll need a 1 and vice versa. In the trie, we go to the required bit side. If favorable option is not there, we'll go other side. Doing this all over for i=1 to n, we'll get the maximum XOR possible.

Query too is log2(MAX).
Problem2: Given an array of integers, find the subarray with maximum XOR.
Solution: Let's say F(L,R) is XOR of subarray from L to R. Here we use the property that F(L,R)=F(1,R) XOR F(1,L-1). How? Let's say our subarray with maximum XOR ended at position i. Now, we need to maximise F(L,i) ie. F(1,i) XOR F(1,L-1) where L<=i. Suppose, we inserted F(1,L-1) in our trie for all L<=i, then it's just problem1.
ans=0
pre=0
Trie.insert(0)
for i=1 to N:
pre = pre XOR a[i]
Trie.insert(pre)
ans=max(ans, Trie.query(pre))
print ans
You can try this problem here: ACM-ICPC Live Archive
Problem3: Given an array of positive integers you have to print the number of subarrays whose XOR is less than K.
Solution: This again uses the concepts we have seen till now. We'll just go like previous question. For each index i=1 to N, we can count how many subarrays ending at ith position satisfy the given condition.
ans=0
p=0
for i=1 to N:
q=p XOR A[i]
ans += Trie.query(q,k)
Trie.insert(q)
p=q
query(q,k) returns how many integers already exist into structure which when taken xor with q return an integer less than k. We compare the corresponding bits of q and k, beginning from most significant bits. Suppose p and q are the respective bits we are considering now.
If q is 1, and p is 0, then we do this:

Similarly we can very easily work out other 3 cases ie. (q=1,p=1), (q=0,p=1) and (q=0,p=1).
So, we need to alter our structure here, we also keep the number of leaf nodes reachable from current node if I go to the left side and similarly for right side. Because, otherwise, the complexity will increase, if we traverse the whole tree again and again. We can do this while inserting numbers into the tree very easily.
This problem was set in CodeCraft'14. You can pratice here: SPOJ.com - Problem SUBXOR
Now, let's talk about implementations. For implementation of a trie in C/CPP we can keep nodes and left and right pointers. We can write recursive functions.
insert(root, num, level):
if level==-1: return root
x=level'th bit of num
if x==1:
if root->right is NULL: create root->right
else: insert(root->right,num,level-1)
else:
if root->left is NULL: create root->left
else: insert(root->left,num,level-1)
For queries also, we recursively traverse the tree.
Update: Another problem using Trie(yay! :P). Problem - B - Codeforces
Sub-Problem: Given a group of n non-empty strings. During the game two players build the word together, initially the word is empty. The players move in turns. On his step player must add a single letter in the end of the word, the resulting word must be prefix of at least one string from the group. A player loses if he cannot move.
We need to find which player(first or second) has the winning strategy.
So, the idea here is again to build a trie of all strings. Why? Because a trie stores information about all prefixes. Now, we will try to evaluate for each node if first player has a winning strategy or not. We can do this recursively. For a node v, for each node u such that u is a immediate child of v, if first player has a losing strategy for u, then for node v first player has a winning strategy. For example, say we have "abc", "abd", "acd". Our trie would look like:
 All leaf nodes have winning strategy.
All leaf nodes have winning strategy.