Print Matrix Diagonally

https://www.geeksforgeeks.org/zigzag-or-diagonal-traversal-of-matrix/

Given a 2D matrix, print all elements of the given matrix in diagonal order. For example, consider the following 5 X 4 input matrix.

    1     2     3     4
    5     6     7     8
    9    10    11    12
   13    14    15    16
   17    18    19    20

Diagonal printing of the above matrix is

    1
    5     2
    9     6     3
   13    10     7     4
   17    14    11     8
   18    15    12
   19    16
   20

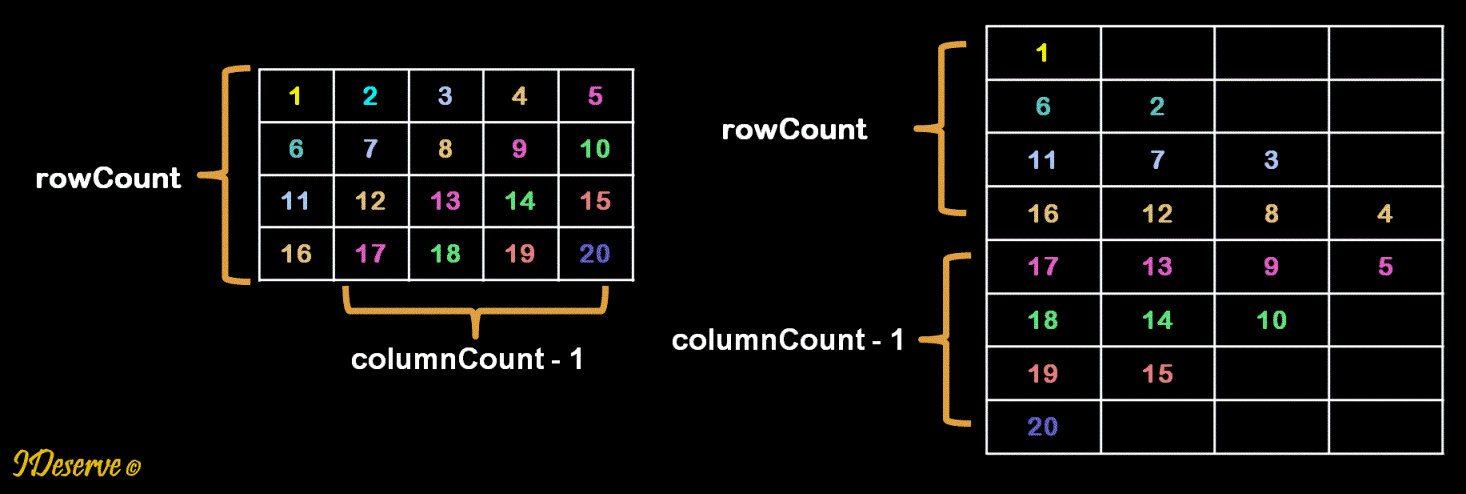
The diagonal printing of a given matrix “matrix[ROW][COL]” always has “ROW + COL – 1” lines in output.

https://www.ideserve.co.in/learn/print-matrix-diagonally

Then, number of diagonals will be = rowCount + columnCount - 1 as depicted in the diagram below.

Step 1 details: Print first rowCount diagonals 
Iterate to print diagonals from row k = 0 to rowCount - 1.
1: Start with row = k and col = 0
2: Print the element matrix[row][col]
3: Decrement row by 1, increment col by 1 till row >= 0 and  col < columnCount

Step 2 details: Print next columnCount - 1 diagonals 
Iterate to print diagonals from column k = 1 to columnCount - 1
1: Start with last row, row = rowCount - 1 and col = k
2: Print the element matrix[row][col]
3: Decrement row by 1, increment col by 1 till row >= 0 and  col < columnCount

    public static void printMatrixDiagonally(int[][] matrix) {

 

        int row, col;

        int rowCount = matrix.length;

        int columnCount = matrix[0].length;

 

        for (int k = 0; k < rowCount; k++) {

            for (row = k, col = 0; row >= 0 && col < columnCount; row--, col++) {

                System.out.print(matrix[row][col] + " ");

            }

            System.out.println();

        }

 

        for (int k = 1; k < columnCount; k++) {

            for (row = rowCount - 1, col = k; row >= 0 && col < columnCount; row--, col++) {

                System.out.print(matrix[row][col] + " ");

            }

            System.out.println();

        }

http://javabypatel.blogspot.com/2016/12/print-matrix-diagonally-or-diagonal.html

// The main function that prints given matrix in diagonal order

void diagonalOrder(int matrix[][COL])

{

    // There will be ROW+COL-1 lines in the output

    for (int line=1; line<=(ROW + COL -1); line++)

    {

        /* Get column index of the first element in this line of output.

           The index is 0 for first ROW lines and line - ROW for remaining

           lines  */

        int start_col =  max(0, line-ROW);

        /* Get count of elements in this line. The count of elements is

           equal to minimum of line number, COL-start_col and ROW */

         int count = min(line, (COL-start_col), ROW);

        /* Print elements of this line */

        for (int j=0; j<count; j++)

            printf("%5d ", matrix[min(ROW, line)-j-1][start_col+j]);

        /* Ptint elements of next diagonal on next line */

        printf("\n");

    }

}

Below is an Alternate Method to solve the above problem.

Matrix =>       1     2     3     4
                5     6     7     8
                9     10    11   12
                13    14    15   16
                17    18    19   20 
   
Observe the sequence
          1 /  2 /  3 /  4
           / 5  /  6 /  7 /  8
               /  9 / 10 / 11 / 12
                   / 13 / 14 / 15 / 16
                       / 17 / 18 / 19 / 20

     public static int R,C;

       

     private static void diagonalOrder(int[][] arr) {

           

             /* through this for loop we choose each element

             of first column as starting point and print 

             diagonal starting at it. arr[0][0], arr[1][0]

             ....arr[R-1][0] are all starting points */

             for (int k = 0; k < R; k++)

             {

                 System.out.print(arr[k][0] + " ");

                   

                 int i = k - 1;    // set row index for next

                                   // point in diagonal

                 int j = 1;       //  set column index for 

                                  // next point in diagonal

            

                 /* Print Diagonally upward */

                 while (isValid(i, j))

                 {

                     System.out.print(arr[i][j] + " ");

                       

                     i--;

                     j++;    // move in upright direction

                 }

                   

                 System.out.println("");

             }

            

             /* through this for loop we choose each element

                of last row as starting point (except the 

                [0][c-1] it has already been processed in 

                previous for loop) and print diagonal 

                starting at it. arr[R-1][0], arr[R-1][1]....

                arr[R-1][c-1] are all starting points */

            

             // Note : we start from k = 1 to C-1;

             for (int k = 1; k < C; k++)

             {

                 System.out.print(arr[R-1][k] + " ");

                   

                 int i = R - 2; // set row index for next 

                                // point in diagonal

                 int j = k + 1; // set column index for  

                                // next point in diagonal

            

                 /* Print Diagonally upward */

                 while (isValid(i, j))

                 {

                     System.out.print(arr[i][j] + " ");

                       

                     i--;

                     j++; // move in upright direction

                 }

                   

                 System.out.println("");

             }

         }

              

    public static  boolean isValid(int i, int j)

     {

         if (i < 0 || i >= R || j >= C || j < 0) return false;

         return true;

     }

Read full article from Print Matrix Diagonally | GeeksforGeeks