http://massivealgorithms.blogspot.com/2014/06/chain-matrix-multiplication.html
https://www.8bitavenue.com/dynamic-programming-matrix-chain-multiplication/
Dynamic Programming | Set 8 (Matrix Chain Multiplication) | GeeksforGeeks
Given a sequence of matrices, find the most efficient way to multiply these matrices together.
let the chain be ABCD, then there are 3 way to place first set of parenthesis: A(BCD), (AB)CD and (ABC)D. So when we place a set of parenthesis, we divide the problem into subproblems of smaller size.
Also check http://en.wikipedia.org/wiki/Matrix_chain_multiplication
Time Complexity: O(n^3)
Auxiliary Space: O(n^2)
https://bruceoutdoors.wordpress.com/2015/11/19/matrix-chain-multiplication-with-c-code-part-2-implementation/
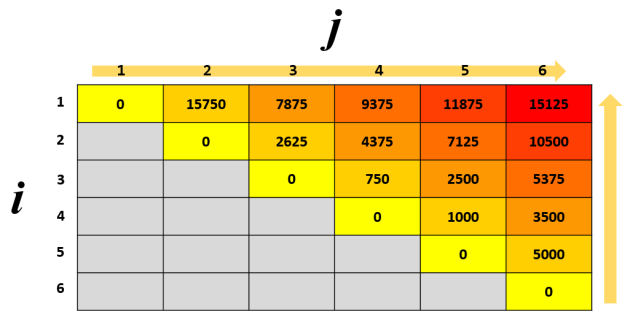
because all the values of all cells where j – i = 1 depends on all cells where j – i = 0. Consequently, all values of all cells where j – i = 2 depends on all cells where j – i = 1 and j – i = 0; you can validate this by plugging in the numbers into the formula. Because all cells aside the base case requires cells below and to its left up until it hits the base case, we can continue filling up the cells of the array DP diagonally until we hit the top right cell.
https://bruceoutdoors.wordpress.com/2015/11/24/matrix-chain-multiplication-with-c-code-part-3-extracting-the-sequence/
http://en.wikipedia.org/wiki/Matrix_chain_multiplication
http://www.sanfoundry.com/java-program-perform-optimal-paranthesization-using-dynamic-programming/
An algorithm published in 1984 by Hu and Shing achieves O(n log n) complexity. They showed how the matrix chain multiplication problem can be transformed (or reduced) into the problem of polygon triangulation.
https://learn.hackerearth.com/tutorial/dynamic-programming/58/matrix-chain-multiplication/
X. Printing brackets in Matrix Chain Multiplication Problem
http://www.geeksforgeeks.org/printing-brackets-matrix-chain-multiplication-problem/
Here we need print parenthssization also.
The idea is to store optimal break point for every subexpression (i, j) in a 2D array bracket[n][n]. Once we have bracket array us constructed, we can print parenthesization
Time Complexity: O(n^3)
Auxiliary Space: O(n^2)
https://bruceoutdoors.wordpress.com/2015/11/24/matrix-chain-multiplication-with-c-code-part-3-extracting-the-sequence/
http://www.8bitavenue.com/2011/11/dynamic-programming-matrix-chain-multiplication/
Read full article from Dynamic Programming | Set 8 (Matrix Chain Multiplication) | GeeksforGeeks
https://www.8bitavenue.com/dynamic-programming-matrix-chain-multiplication/
Dynamic Programming | Set 8 (Matrix Chain Multiplication) | GeeksforGeeks
Given a sequence of matrices, find the most efficient way to multiply these matrices together.
let the chain be ABCD, then there are 3 way to place first set of parenthesis: A(BCD), (AB)CD and (ABC)D. So when we place a set of parenthesis, we divide the problem into subproblems of smaller size.
Input: p[] = {40, 20, 30, 10, 30}
Output: 26000
There are 4 matrices of dimensions 40x20, 20x30, 30x10 and 10x30.
Let the input 4 matrices be A, B, C and D. The minimum number of
multiplications are obtained by putting parenthesis in following way
(A(BC))D --> 20*30*10 + 40*20*10 + 40*10*30
Also check http://en.wikipedia.org/wiki/Matrix_chain_multiplication
Time Complexity: O(n^3)
Auxiliary Space: O(n^2)
https://bruceoutdoors.wordpress.com/2015/11/19/matrix-chain-multiplication-with-c-code-part-2-implementation/
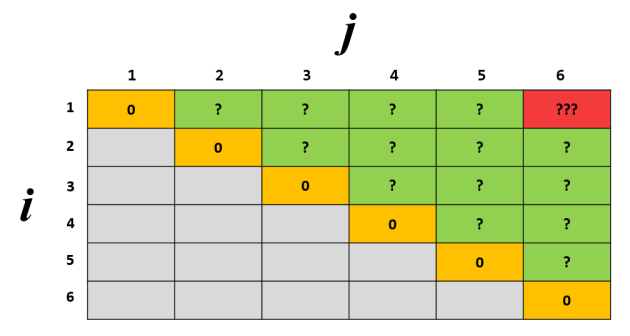
However, this problem is tricky to solve since it involves 2 variables i and j. We need a 2D array to keep track of this. In a single dimensional array ordering is trivial; we simply go from left to right, building the solution from the bottom up, but with 2 dimensions ordering becomes tricky. Which cell do we solve first?
- the base case is when i = j, then B(i, j) = 0.
- i cannot exceed j, so those areas will need to be grayed out.
- B(1, 6) is the solution.
So with that, let us fill up an array DP based on the inputs we have above:
https://bruceoutdoors.wordpress.com/2015/11/24/matrix-chain-multiplication-with-c-code-part-3-extracting-the-sequence/
int MatrixChainOrder(int p[], int n){ int m[n][n]; int i, j, k, L, q; /* m[i,j] = Minimum number of scalar multiplications needed to compute the matrix A[i]A[i+1]...A[j] = A[i..j] where dimention of A[i] is p[i-1] x p[i] */ // cost is zero when multiplying one matrix. for (i = 1; i < n; i++) //\\ m[i][i] = 0; // L is chain length. for (L=2; L<n; L++) { for (i=1; i<=n-L+1; i++) { j = i+L-1; m[i][j] = INT_MAX; for (k=i; k<=j-1; k++) { // q = cost/scalar multiplications q = m[i][k] + m[k+1][j] + p[i-1]*p[k]*p[j]; if (q < m[i][j]) m[i][j] = q; } } } return m[1][n-1];}int MatrixChainOrder(int p[], int i, int j){ if(i == j) return 0; int k; int min = INT_MAX; int count; // place parenthesis at different places between first and last matrix, // recursively calculate count of multiplcations for each parenthesis // placement and return the minimum count for (k = i; k <j; k++) { count = MatrixChainOrder(p, i, k) + MatrixChainOrder(p, k+1, j) + p[i-1]*p[k]*p[j]; if (count < min) min = count; } // Return minimum count return min;}http://www.sanfoundry.com/java-program-perform-optimal-paranthesization-using-dynamic-programming/
public class MatrixOrderOptimization { protected int[][]m; protected int[][]s; public void matrixChainOrder(int[] p) { int n = p.length - 1; m = new int[n][n]; s = new int[n][n]; for (int ii = 1; ii < n; ii++) { for (int i = 0; i < n - ii; i++) { int j = i + ii; m[i][j] = Integer.MAX_VALUE; //\\ for (int k = i; k < j; k++) { int q = m[i][k] + m[k+1][j] + p[i]*p[k+1]*p[j+1]; if (q < m[i][j]) { m[i][j] = q; s[i][j] = k; } } } } } public void printOptimalParenthesizations() { boolean[] inAResult = new boolean[s.length]; printOptimalParenthesizations(s, 0, s.length - 1, inAResult); } void printOptimalParenthesizations(int[][]s, int i, int j, /* for pretty printing: */ boolean[] inAResult) { if (i != j) { printOptimalParenthesizations(s, i, s[i][j], inAResult); printOptimalParenthesizations(s, s[i][j] + 1, j, inAResult); String istr = inAResult[i] ? "_result " : " "; String jstr = inAResult[j] ? "_result " : " "; System.out.println(" A_" + i + istr + "* A_" + j + jstr); inAResult[i] = true; inAResult[j] = true; } } }
An algorithm published in 1984 by Hu and Shing achieves O(n log n) complexity. They showed how the matrix chain multiplication problem can be transformed (or reduced) into the problem of polygon triangulation.
https://learn.hackerearth.com/tutorial/dynamic-programming/58/matrix-chain-multiplication/
X. Printing brackets in Matrix Chain Multiplication Problem
http://www.geeksforgeeks.org/printing-brackets-matrix-chain-multiplication-problem/
Here we need print parenthssization also.
The idea is to store optimal break point for every subexpression (i, j) in a 2D array bracket[n][n]. Once we have bracket array us constructed, we can print parenthesization
Time Complexity: O(n^3)
Auxiliary Space: O(n^2)
https://bruceoutdoors.wordpress.com/2015/11/24/matrix-chain-multiplication-with-c-code-part-3-extracting-the-sequence/
To do this we keep track of the point at which we split up the chain as prefix and suffix: the point k (we define this from the previous post). We do this by storing it in another 2D array of the same size as DP, which we call splits:
1
2
3
4
5
| int ops = DP[i][k] + DP[k + 1][j] + rc[i] * rc[k + 1] * rc[j + 1];if (ops < DP[i][j]) { DP[i][j] = ops; splits[i][j] = k;} |
// Function for printing the optimal// parenthesization of a matrix chain productvoid printParenthesis(int i, int j, int n, int *bracket, char &name){ // If only one matrix left in current segment if (i == j) { cout << name++; return; } cout << "("; // Recursively put brackets around subexpression // from i to bracket[i][j]. // Note that "*((bracket+i*n)+j)" is similar to // bracket[i][j] printParenthesis(i, *((bracket+i*n)+j), n, bracket, name); // Recursively put brackets around subexpression // from bracket[i][j] + 1 to j. printParenthesis(*((bracket+i*n)+j) + 1, j, n, bracket, name); cout << ")";}// Matrix Ai has dimension p[i-1] x p[i] for i = 1..n// Please refer below article for details of this// functionvoid matrixChainOrder(int p[], int n){ /* For simplicity of the program, one extra row and one extra column are allocated in m[][]. 0th row and 0th column of m[][] are not used */ int m[n][n]; // bracket[i][j] stores optimal break point in // subexpression from i to j. int bracket[n][n]; /* m[i,j] = Minimum number of scalar multiplications needed to compute the matrix A[i]A[i+1]...A[j] = A[i..j] where dimension of A[i] is p[i-1] x p[i] */ // cost is zero when multiplying one matrix. for (int i=1; i<n; i++) m[i][i] = 0; // L is chain length. for (int L=2; L<n; L++) { for (int i=1; i<n-L+1; i++) { int j = i+L-1; m[i][j] = INT_MAX; for (int k=i; k<=j-1; k++) { // q = cost/scalar multiplications int q = m[i][k] + m[k+1][j] + p[i-1]*p[k]*p[j]; if (q < m[i][j]) { m[i][j] = q; // Each entry bracket[i,j]=k shows // where to split the product arr // i,i+1....j for the minimum cost. bracket[i][j] = k; } } } } // The first matrix is printed as 'A', next as 'B', // and so on char name = 'A'; cout << "Optimal Parenthesization is : "; printParenthesis(1, n-1, n, (int *)bracket, name); cout << "\nOptimal Cost is : " << m[1][n-1];}Read full article from Dynamic Programming | Set 8 (Matrix Chain Multiplication) | GeeksforGeeks