Viterbi algorithm

https://en.wikipedia.org/wiki/Viterbi_algorithm

The Viterbi algorithm is a dynamic programming algorithm for finding the most likely sequence of hidden states – called the Viterbi path – that results in a sequence of observed events, especially in the context of Markov information sources and hidden Markov models.

Consider a village where all villagers are either healthy or have a fever and only the village doctor can determine whether each has a fever. The doctor diagnoses fever by asking patients how they feel. The villagers may only answer that they feel normal, dizzy, or cold.

The doctor believes that the health condition of his patients operate as a discrete Markov chain. There are two states, "Healthy" and "Fever", but the doctor cannot observe them directly, they are hidden from him. On each day, there is a certain chance that the patient will tell the doctor he/she is "normal", "cold", or "dizzy", depending on her health condition.

The observations (normal, cold, dizzy) along with a hidden state (healthy, fever) form a hidden Markov model (HMM), and can be represented as follows in the Python programming language:

states = ('Healthy', 'Fever')
 
observations = ('normal', 'cold', 'dizzy')
 
start_probability = {'Healthy': 0.6, 'Fever': 0.4}
 
transition_probability = {
   'Healthy' : {'Healthy': 0.7, 'Fever': 0.3},
   'Fever' : {'Healthy': 0.4, 'Fever': 0.6}
   }
 
emission_probability = {
   'Healthy' : {'normal': 0.5, 'cold': 0.4, 'dizzy': 0.1},
   'Fever' : {'normal': 0.1, 'cold': 0.3, 'dizzy': 0.6}
   }

In this piece of code, start_probability represents the doctor's belief about which state the HMM is in when the patient first visits (all he knows is that the patient tends to be healthy). The particular probability distribution used here is not the equilibrium one, which is (given the transition probabilities) approximately {'Healthy': 0.57, 'Fever': 0.43}. The transition_probability represents the change of the health condition in the underlying Markov chain. In this example, there is only a 30% chance that tomorrow the patient will have a fever if he is healthy today. The emission_probability represents how likely the patient is to feel on each day. If he is healthy, there is a 50% chance that he feels normal; if he has a fever, there is a 60% chance that he feels dizzy.

Graphical representation of the given HMM

The patient visits three days in a row and the doctor discovers that on the first day she feels normal, on the second day she feels cold, on the third day she feels dizzy. The doctor has a question: what is the most likely sequence of health conditions of the patient that would explain these observations? This is answered by the Viterbi algorithm.

When implementing Viterbi's algorithm, it should be noted that many languages use floating point arithmetic - as p is small, this may lead tounderflow in the results. A common technique to avoid this is to take the logarithm of the probabilities and use it throughout the computation, the same technique used in the Logarithmic Number System. Once the algorithm has terminated, an accurate value can be obtained by performing the appropriate exponentiation.

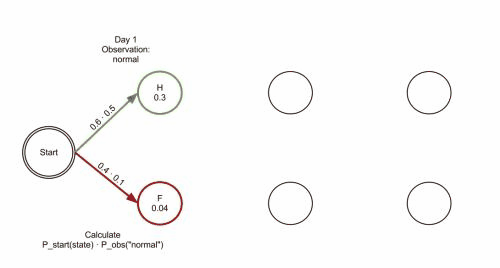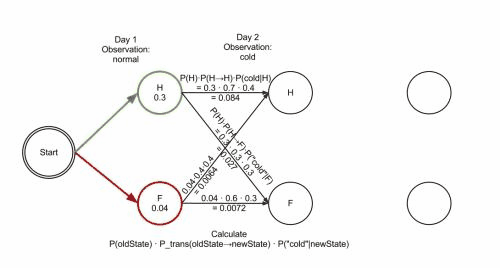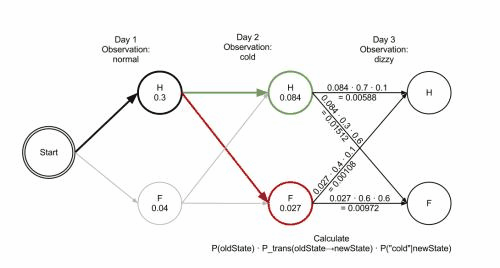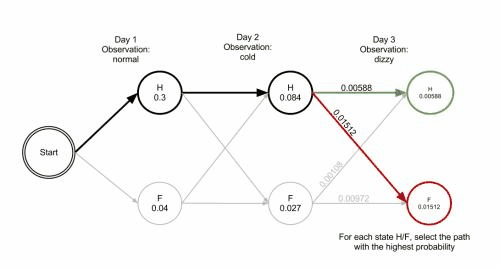
The operation of Viterbi's algorithm can be visualized by means of a trellis diagram. The Viterbi path is essentially the shortest path through this trellis. The trellis for the clinic example is shown below; the corresponding Viterbi path is in bold:

Animation of the trellis diagram for the Viterbi algorithm. After Day 3, the most likely path is['Healthy', 'Healthy', 'Fever']

https://en.wikibooks.org/wiki/Algorithm_Implementation/Viterbi_algorithm

public class Viterbi 
{
 static final String HEALTHY = "Healthy";
 static final String FEVER = "Fever";

 static final String DIZZY = "dizzy";
 static final String COLD = "cold";
 static final String NORMAL = "normal";

 public static void main(String[] args) 
 {
  String[] states = new String[] {HEALTHY, FEVER};
 
  String[] observations = new String[] {DIZZY, COLD, NORMAL};
 
  Hashtable<String, Float> start_probability = new Hashtable<String, Float>();
  start_probability.put(HEALTHY, 0.6f);
  start_probability.put(FEVER, 0.4f);
 
  // transition_probability
  Hashtable<String, Hashtable<String, Float>> transition_probability = 
   new Hashtable<String, Hashtable<String, Float>>();
   Hashtable<String, Float> t1 = new Hashtable<String, Float>();
   t1.put(HEALTHY, 0.7f);
   t1.put(FEVER, 0.3f);
   Hashtable<String, Float> t2 = new Hashtable<String, Float>();
   t2.put(HEALTHY, 0.4f);
   t2.put(FEVER, 0.6f);
  transition_probability.put(HEALTHY, t1);
  transition_probability.put(FEVER, t2);
 
  // emission_probability
  Hashtable<String, Hashtable<String, Float>> emission_probability = 
   new Hashtable<String, Hashtable<String, Float>>();
   Hashtable<String, Float> e1 = new Hashtable<String, Float>();
   e1.put(DIZZY, 0.1f);  
   e1.put(COLD, 0.4f); 
   e1.put(NORMAL, 0.5f);
   Hashtable<String, Float> e2 = new Hashtable<String, Float>();
   e2.put(DIZZY, 0.6f);  
   e2.put(COLD, 0.3f); 
   e2.put(NORMAL, 0.1f);
  emission_probability.put(HEALTHY, e1);
  emission_probability.put(FEVER, e2);
 
  Object[] ret = forward_viterbi(observations,
                           states,
                           start_probability,
                           transition_probability,
                           emission_probability);
  System.out.println(((Float) ret[0]).floatValue());  
  System.out.println((String) ret[1]);
  System.out.println(((Float) ret[2]).floatValue());
 }
 
 public static Object[] forward_viterbi(String[] obs, String[] states,
   Hashtable<String, Float> start_p,
   Hashtable<String, Hashtable<String, Float>> trans_p,
   Hashtable<String, Hashtable<String, Float>> emit_p)
 {
  Hashtable<String, Object[]> T = new Hashtable<String, Object[]>();
  for (String state : states)
   T.put(state, new Object[] {start_p.get(state), state, start_p.get(state)});
 
  for (String output : obs)
  {
   Hashtable<String, Object[]> U = new Hashtable<String, Object[]>();
   for (String next_state : states)
   {
    float total = 0;
    String argmax = "";
    float valmax = 0;
 
    float prob = 1;
    String v_path = "";
    float v_prob = 1; 
 
    for (String source_state : states)
    {
     Object[] objs = T.get(source_state);
     prob = ((Float) objs[0]).floatValue();
     v_path = (String) objs[1];
     v_prob = ((Float) objs[2]).floatValue();
 
     float p = emit_p.get(source_state).get(output) *
         trans_p.get(source_state).get(next_state);
     prob *= p;
     v_prob *= p;
     total += prob;
     if (v_prob > valmax)
     {
      argmax = v_path + "," + next_state;
      valmax = v_prob;
     }
    }
    U.put(next_state, new Object[] {total, argmax, valmax});
   }
   T = U;   
  }
 
  float total = 0;
  String argmax = "";
  float valmax = 0;
 
  float prob;
  String v_path;
  float v_prob;
 
  for (String state : states)
  {
   Object[] objs = T.get(state);
   prob = ((Float) objs[0]).floatValue();
   v_path = (String) objs[1];
   v_prob = ((Float) objs[2]).floatValue();
   total += prob;
   if (v_prob > valmax)
   {
    argmax = v_path;
    valmax = v_prob;
   }
  } 
  return new Object[]{total, argmax, valmax}; 
 }
}

The function viterbi takes the following arguments: obs is the sequence of observations, e.g. ['normal', 'cold', 'dizzy'];states is the set of hidden states; start_p is the start probability; trans_p are the transition probabilities; and emit_p are the emission probabilities. 

http://blog.csdn.net/laoliulaoliu/article/details/7559145

假设你有一个朋友在外地，每天你可以通过电话来了解他每天的活动。他每天只会做三种活动之一——Walk, Shop, Clean。你的朋友从事哪一种活动的概率与当地的气候有关，这里，我们只考虑两种天气——Rainy, Sunny。我们知道，天气与运动的关系如下：

	Rainy	Sunny
Walk	0.1	0.6
Shop	0.4	0.3
Clean	0.5	0.1

例如，在下雨天出去散步的可能性是0.1。

而天气之前互相转换的关系如下，（从行到列）

	Rainy	Sunny
Rainy	0.7	0.3
Sunny	0.4	0.6

例如，从今天是晴天而明天就开始下雨的可能性是0.4 。

同时为了求解问题我们假设初始情况：通话开始的第一天的天气有0.6的概率是Rainy，有0.4概率是Sunny。OK，现在的问题是，如果连续三天，你发现你的朋友的活动是：Walk->Shop->Clean；那么，如何判断你朋友那里这几天的天气是怎样的？

"""
 X = ['Rainy', 'Sunny'] = [0, 1]
 y = ['Walk', 'Shop', 'Clean'] = [0, 1, 2]

  天气状态转移:
  Rainy -> Rainy = 0.7, Rainy -> Sunny = 0.3
  Sunny -> Rainy = 0.4, Sunny -> Sunny = 0.6
  tp = [[0.7, 0.3], [0.4, 0.6]]

  某天气下某行动的概率：
  Walk|Rainy = 0.1, Shop|Rainy = 0.4, Clean|Rainy = 0.5
  Walk|Sunny = 0.6, Shop|Sunny = 0.3, Clean|Sunny = 0.1
  ep = [[0.1, 0.4, 0.5], [0.6, 0.3, 0.1]]

  第一天天气的概率：
  Rainy = 0.6, Sunny = 0.4
  sp = [0.6, 0.4]
"""

def forward_viterbi(y, X, sp, tp, ep):
    T = {}
    for state in X:
        ##  (prob,  V.path, V.prob )
        T[state] = (sp[state], [state], sp[state])
    for output in y:
        U = {}
        for next_state in X:
            total = 0
            argmax = None
            valmax = 0
            for source_state in X:
                (prob, v_path, v_prob) = T[source_state]
                p = ep[source_state][output] * tp[source_state][next_state]
                prob *= p
                v_prob *= p
                total += prob
                if v_prob > valmax:
                    argmax = v_path + [next_state]
                    valmax = v_prob
            U[next_state] = (total, argmax, valmax)
        T = U

    ## apply sum/max to the final states:
    total = 0
    argmax = None
    valmax = 0
    for state in X:
        (prob, v_path, v_prob) = T[state]
        total += prob
        if v_prob > valmax:
            argmax = v_path
            valmax = v_prob
    return (total, argmax, valmax)

if __name__ == '__main__':
    X = [0, 1]
    y = [0, 1, 2]
    sp = [0.6, 0.4]
    tp = [[0.7, 0.3], [0.4, 0.6]]
    ep = [[0.1, 0.4, 0.5], [0.6, 0.3, 0.1]]
    ret = forward_viterbi(y, X, sp, tp, ep)
    print(ret)

output：(0.033611999999999996, [1, 0, 0, 0], 0.009407999999999998)

所以朋友那边这几天最可能的天气情况是Sunny->Rainy->Rainy->Rainy，它有0.009408的概率出现。而我们算法的另一个附带的结论是，我们所观察到的朋友这几天的活动序列：Walk->Shop->Clean在我们的隐马可夫模型之下出现的总概率是0.033612（也是Forward算法的输出）。
算法对于每一个状态要记录一个三元组：(prob, v_path, v_prob)，其中，prob是从开始状态到当前状态所有路径（不仅仅 是最有可能的viterbi路径）的概率加在一起的结果（作为算法附产品，它可以输出一个观察序列在给定HMM下总的出现概率，即forward算法的输出），v_path是从开始状态一直到当前状态的viterbi路径，v_prob则是该路径的概率。
算法开始，初始化T （T是一个Map，将每一种可能状态映射到上面所说的三元组上）
三重循环，对每个一活动y，考虑下一步每一个可能的状态next_state，并重新计算若从T中的当前状态state跃迁到next_state概率会有怎样的变化。跃迁主要考虑天气转移（tp[source_state][next_state]）与该天气下从事某种活动（ep[source_state][output]）的联合概率。所有下一步状态考虑完后，要从T中找出最优的选择viterbi路径——即概率最大的viterbi路径，即上面更新Map U的代码U[next_state] = (total, argmax, valmax)。
算法最后还要对T中的各种情况总结，对total求和，选择其中一条作为最优的viterbi路径。
算法输出四个天气状态，这是因为，计算第三天的概率时，要考虑天气转变到下一天的情况。
http://blog.csdn.net/jinzhichaoshuiping/article/details/47285767

1.马尔可夫模型

这个模型的每一个状态都只依赖于前一个状态，这个条件称之为“马尔可夫假设”。

存在X1, ... , Xn 的一个数列，这些变量的范围，即他们所有可能取值的集合，成为“状态空间”，在天气状况的例子中，X1, ... , Xn表示的是第一天...第n天的天气状况，状态空间为“晴天，阴天，雨天”。

如果Xn+1 满足等式：

                                                        

则称该数列具有马尔可夫性质，这种具有马尔可夫性质的离散随机过程称为马尔可夫过程。

该过程中，每个状态的转移只依赖于之前的 n 个状态，这个过程被称为1个 n 阶的模型，其中 n 是影响转移状态的数目。最简单的马尔科夫过程就是一阶过程，每一个状态的转移只依赖于其之前的那一个状态。注意这和确定性系统不一样，因为这种转移是有概率的，而不是确定性的。

对于天气状况的这个例子来说，所有可能的一阶转移为：

                                                                                  

每一个转移的概率称为状态转移概率，将这些状态转移概率用3*3的状态转移矩阵来表示为：         

                                                       

设每一元素为aij。

                                                                                   

矩阵的约束条件：

                                                                                         

这个矩阵表示，如果昨天是晴天，那么今天有50%的可能是晴天，37.5%的概率是阴天，12.5%的概率会下雨，很明显，矩阵中每一行的和都是1。

为了初始化这样一个系统，我们需要一个初始的概率向量：

                                                                                                          

这个向量表示第一天是晴天。

到这里，我们就为上面的一阶马尔科夫过程定义了以下三个部分：

状态：晴天、阴天和下雨

初始向量：定义系统在时间为0的时候的状态的概率

状态转移矩阵：每种天气转换的概率

所有的能被这样描述的系统都是一个马尔科夫过程。

那么对于一个关在监狱里的人来说，他看不到外面的天气是怎样的，但是聪明的人有自己的办法。研究表明，海藻的状态在某种概率上是和天气的情况相关的。于是监狱里的人便可以通过监狱里藻类的状态来推断外面天气的状态。

在这个事件中，便存在两个状态集合，一个是可观察到的状态的集合（藻类的状态），一个是隐藏的状态（天气状况）。此时的天气状况便成为了一个隐藏的马尔可夫过程。

将一个隐藏的马尔可夫过程和一个与这个隐藏马尔科夫过程概率相关的并且可以观察到的状态集合建立模型，便是隐马尔可夫模型。

                                                          

海藻的状态和天气的状况存在的概率关系称之为混淆矩阵。

                                                                     

这样的隐马尔可夫模型可以用一个5元组来表示，其中 N 表示隐藏状态的数量，我们要么知道确切的值，要么猜测该值，M 表示可观测状态的数量，可以通过训练集获得， π={πi} 为初始状态概率，A={aij} 为隐藏状态的转移矩阵 Pr(xt(i) | xt-1(j))，B={bik} 表示某个时刻因隐藏状态而可观察的状态的概率，即混淆矩阵，Pr(ot(i) | xt(j))。在状态转移矩阵和混淆矩阵中的每个概率都是时间无关的，即当系统演化时，这些矩阵并不随时间改变。对于一个 N 和 M 固定的 HMM 来说，用 λ={ π, A, B } 表示 HMM 参数。

                                         

所以在一个隐马尔可夫模型中存在3个要素：

1.计算给定的一个可观察序列的概率

2.根据可观察序列找到最可能的隐藏状态序列。

3.根据可观察的序列找到最可能的HMM。即求出HMM中的各个参数。

下面就是一一解决这三个问题，分别用到了三个算法：前向算法，Viterbi算法，Baum-Welch算法。

http://blog.csdn.net/jinzhichaoshuiping/article/details/47318513

与之前的前向算法一样，先计算部分概率，然后在计算剩下的概率。与前向算法不同的是在t时刻最可能到达的某个状态的一条路径的概率，而不是所有的概率之和。

每一个状态都存在一个概率最大的路径，这个路径是最优路径。称之为部分最优路径，概率称之为部分概率。对于每一个时刻的每一个状态都存在这样一个路径和这样一个概率。

最后需要的得到的是t=T时刻的每一个状态的部分最优路径和这个路劲的部分概率。选择概率最大的状态的部分最优路径便是全局的最优路径。

1.初始状态t=1时刻部分概率

  这个时候不存路径，所以需要初始状态概率π={πi}乘以混淆矩阵。

                                                                                 

2.计算t>1时刻的部分概率

采用的是递归的计算方法，所以在计算t时刻的部分概率，只需要知道t-1时刻的部分概率。

                                                               

计算所有到状态X的概率，找到其中最可能的路径，只可能是下列三种路径之一。

1.(状态序列)，. . .，A，X

2.(状态序列)，. . .，B，X

3.(状态序列)，. . .，C，X

计算公式：Pr (到达A的最优路径) . Pr (X | A) . Pr (观察状态 | X)

                           

Pr（it-1）：t-1时刻某一状态的部分概率

Pr（X|i）：t时刻在t-1时刻状态为i的条件下，状态为x的概率。也就是HMM中的状态转移矩阵。

Pr（observationt |X）：t时刻的观察状态在隐藏状态为x条件下的概率，也就是HMM中的混淆矩阵。

于是得到下列公式：

                                                                      

2.3后向指针

通过之前的过程，得出的是最优路径的概率，但是最优的路径是怎样的，还是不清楚，我们需要一个方法得到最优路径的每一个节点，这便需要用到后向指针。

                                                               

δt-1 (j)：t-1时刻状态为j的最优概率

aij ：由状态t-1时刻的状态j转移到t时刻状态i的状态转移概率

http://blog.csdn.net/jeiwt/article/details/8076739
寻找最可能的隐藏状态序列 (Finding most probable sequence of hidden states)
对于一个特殊的隐马尔科夫模型(HMM)及一个相应的观察序列，我们常常希望能找到生成此序列最可能的隐藏状态序列。