Remove BST keys outside the given range

Related: LeetCode 669 - Trim a Binary Search Tree
Remove BST keys outside the given range | GeeksforGeeks

Given a Binary Search Tree (BST) and a range [min, max], remove all keys which are outside the given range. The modified tree should also be BST. For example, consider the following BST and range [-10, 13].

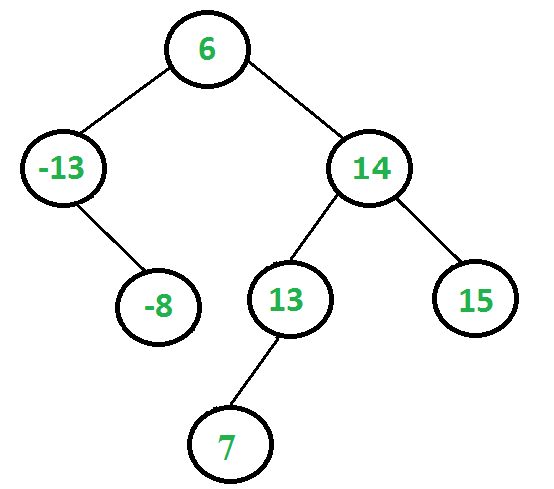
The given tree should be changed to following. Note that all keys outside the range [-10, 13] are removed and modified tree is BST.

There are two possible cases for every node.
1) Node’s key is outside the given range. This case has two sub-cases.
…….a) Node’s key is smaller than the min value.
…….b) Node’s key is greater that the max value.
2) Node’s key is in range.

We don’t need to do anything for case 2. In case 1, we need to remove the node and change root of sub-tree rooted with this node.
The idea is to fix the tree in Postorder fashion. When we visit a node, we make sure that its left and right sub-trees are already fixed. In case 1.a), we simply remove root and return right sub-tree as new root. In case 1.b), we remove root and return left sub-tree as new root.

https://prismoskills.appspot.com/lessons/Binary_Trees/Remove_nodes_outside_a_given_range.jsp

https://www.ideserve.co.in/learn/remove-out-of-range-bst-nodes

    private BinarySearchTreeNode removeOutOfRangeNodes(BinarySearchTreeNode currentNode, int min, int max)

    {

        if (currentNode == null)

        {

            return null;

        }

         

        // correct left and right sub-trees first

        currentNode.left  = removeOutOfRangeNodes(currentNode.left, min, max);

        currentNode.right = removeOutOfRangeNodes(currentNode.right, min, max);

         

        /*

         * if currentNode's value is less than min threshold, it's left sub-tree would already be null

         * simply return reference to right sub-tree

         */

        if (currentNode.data < min)

        {

            return currentNode.right;

        }

 

        /*

         * if currentNode's value is more than max threshold, it's right sub-tree would already be null

         * simply return reference to left sub-tree

         */

        if (currentNode.data > max)

        {

            return currentNode.left;

        }

         

        return currentNode;

    }

     

https://www.techiedelight.com/remove-nodes-bst-keys-outside-valid-range/

public static Node truncate(Node root, int min, int max)

{

// base case

if (root == null) {

return root;

}

// recursively truncate left and right subtree first

root.left = truncate(root.left, min, max);

root.right = truncate(root.right, min, max);

// if root's key is smaller than the minimum allowed, delete it

if (root.data < min) {

root = root.right;

}

// if root's key is larger than the maximum allowed, delete it

else if (root.data > max) {

root = root.left;

}

return root;

}

http://www.ardendertat.com/2012/01/17/programming-interview-questions-26-trim-binary-search-tree/
The complexity of this algorithm is O(N), where N is the number of nodes in the tree. Because we basically perform a post-order traversal of the tree, visiting each and every node one. This is optimal because we should visit every node at least once. - See more at: http://www.ardendertat.com/2012/01/17/programming-interview-questions-26-trim-binary-search-tree/#sthash.7FiPp7EY.dpuf

    private static Node removeOutsideRange(Node root, 

                                           int min, int max) 

    {

        // BASE CASE

        if(root == null)

        {

            return null;

        }

          

        // FIRST FIX THE LEFT AND

        // RIGHT SUBTREE OF ROOT

        root.left = removeOutsideRange(root.left, 

                                       min, max);

        root.right = removeOutsideRange(root.right, 

                                        min, max);

          

        // NOW FIX THE ROOT. THERE ARE 

        // TWO POSSIBLE CASES FOR THE ROOT

        // 1. a) Root's key is smaller than

        // min value(root is not in range)

        if(root.key < min) 

        {

            Node rchild = root.right;

            root = null;

            return rchild;

        }

          

        // 1. b) Root's key is greater than 

        // max value (Root is not in range)

        if(root.key > max) 

        {

            Node lchild = root.left;

            root = null;

            return lchild;

        }

          

        // 2. Root in range

        return root;

    }

Read full article from Remove BST keys outside the given range | GeeksforGeeks