Massive Algorithms: LeetCode 426 - Convert BST to Sorted Doubly Linked List

LeetCode 426 - Convert BST to Sorted Doubly Linked List

Convert a BST to a sorted circular doubly-linked list in-place.
http://tech-queries.blogspot.com/2011/08/convert-binary-tree-in-circular-doubly.html
http://leetcode.com/2010/11/convert-binary-search-tree-bst-to.html
http://shibaili.blogspot.com/2018/08/convert-binary-search-tree-to-sorted.html

Convert a BST to a sorted circular doubly-linked list in-place. Think of the left and right pointers as synonymous to the previous and next pointers in a doubly-linked list.

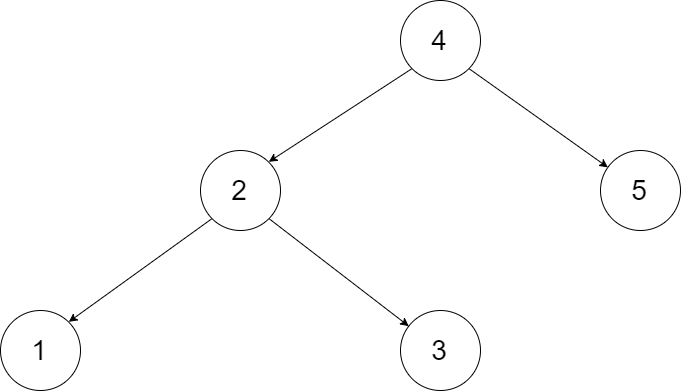
Let's take the following BST as an example, it may help you understand the problem better:

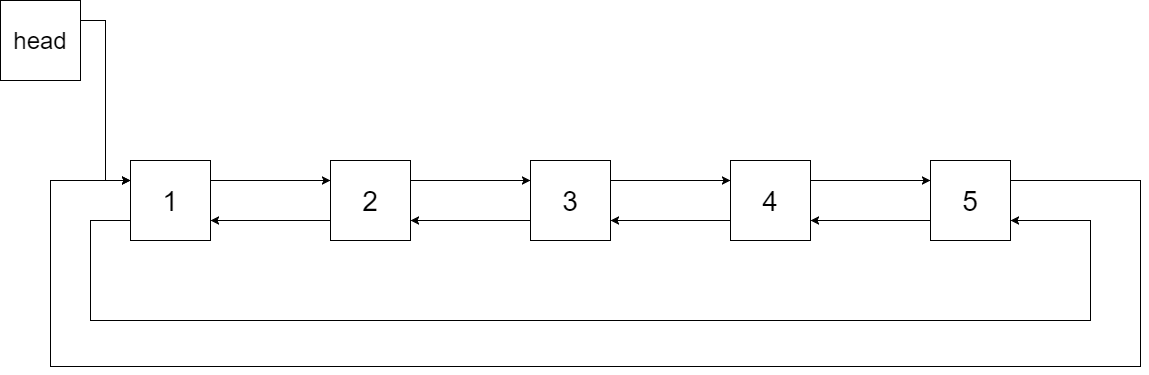
We want to transform this BST into a circular doubly linked list. Each node in a doubly linked list has a predecessor and successor. For a circular doubly linked list, the predecessor of the first element is the last element, and the successor of the last element is the first element.

The figure below shows the circular doubly linked list for the BST above. The "head" symbol means the node it points to is the smallest element of the linked list.

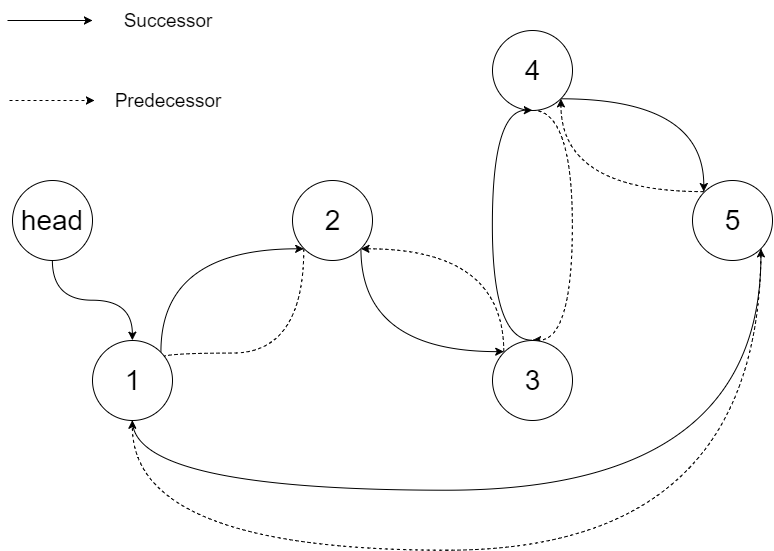
Specifically, we want to do the transformation in place. After the transformation, the left pointer of the tree node should point to its predecessor, and the right pointer should point to its successor. We should return the pointer to the first element of the linked list.

The figure below shows the transformed BST. The solid line indicates the successor relationship, while the dashed line means the predecessor relationship.

http://www.cnblogs.com/grandyang/p/9615871.html

这道题给了我们一个二叉搜索树，让我们将其转化为双向链表。并且题目中给了我们一个带图的例子，帮助我们来理解。题目本身并不难理解，我们需要仔细观察下给的示例图。首先，转化成双向链表的每个结点都有left和right指针指向左右两个结点，不管其原来是否是叶结点还是根结点，转换后统统没有区别。其次，我们发现这是个循环双向链表，即首尾结点是相连的，原先的二叉搜索树中的最左结点和最右结点，现在也互相连接起来了。最后，我们发现返回的结点不再是原二叉搜索树的根结点root了，而是最左结点，即最小值结点。

好，发现了上述规律后，我们来考虑如何破题。根据博主多年经验，跟二叉搜索树有关的题，肯定要利用其性质，即左<根<右，即左子结点值小于根结点值小于右子结点值。而且十有八九都得用中序遍历来解，因为中序遍历的顺序就是左根右啊，跟性质吻合。我们观察原二叉搜索树中结点4连接着结点2和结点5，而在双向链表中，连接的是结点3和结点5，这就是为啥我们要用中序遍历了，因为只有中序遍历，结点3之后才会遍历到结点4，这时候我们可以将结点3和结点4串起来。决定了用中序遍历之后，就要考虑是迭代还是递归的写法，博主建议写递归的，一般写起来都比较简洁，而且递归是解树类问题的神器啊，十有八九都是用递归，一定要熟练掌握。再写中序遍历之前，其实还有难点，因为我们需要把相邻的结点连接起来，所以我们需要知道上一个遍历到的结点是什么，所以用一个变量pre，来记录上一个遍历到的结点。还需要一个变量head，来记录最左结点，这样的话，在递归函数中，先判空，之后对左子结点调用递归，这样会先一直递归到最左结点，此时如果head为空的话，说明当前就是最左结点，赋值给head和pre，对于之后的遍历到的结点，那么可以和pre相互连接上，然后pre赋值为当前结点node，再对右子结点调用递归即可

https://blog.csdn.net/BigFatSheep/article/details/83239067

Node prev = null;

public Node treeToDoublyList(Node root) {

if (root == null){

return null;

}

Node dummy = new Node(0, null, null);

prev = dummy;

helper(root);

//connect tail with head;

prev.right = dummy.right;

dummy.right.left = prev;

return dummy.right;

}

private void helper(Node cur){

if (cur == null){

return;

}

helper(cur.left);

prev.right = cur;

cur.left = prev;

prev = cur;

helper(cur.right);

}

http://shibaili.blogspot.com/2018/08/convert-binary-search-tree-to-sorted.html

    private Node pre = null;

    private Node head = null;

    public Node treeToDoublyList(Node root) {

        if (root == null) return null;

        inorder(root);

        head.left = pre;

        pre.right = head;

        return head;

}

    private void inorder(Node root) {

        if (root == null) {

            return;

}

        inorder(root.left);        

        if (pre == null) {

            head = root;

        }else {

            pre.right = root;

            root.left = pre;    

}

        pre = root;

        inorder(root.right);        

}

X. Divide and conquer

这道题还有一种使用分治法Divide and Conquer来做的方法。分治法，顾名思义，就是把一项任务分成两半，用相同的逻辑去分别处理，之后再粘合起来。混合排序Merge Sort用的也是这种思路。那么我们可以对左右子结点调用递归函数，suppose我们得到了两个各自循环的有序双向链表，然后我们把根结点跟左右子结点断开，将其左右指针均指向自己，这样就形成了一个单个结点的有序双向链表，虽然只是个光杆司令，但人家仍然是有序双向链表，不是沙雕，就问你叼不叼。那么此时我们只要再写一个连接两个有序双向链表的子函数，就可以将这三个有序双向链表按顺序链接起来了。

而链接两个有序双向链表的子函数也简单，首先判空，若一个为空，则返回另一个。如果两个都不为空，则把第一个链表的尾结点的右指针链上第二个链表的首结点，同时第二个链表的首结点的左指针链上第一个链表的尾结点。同理，把第二个链表的尾结点的右指针链上第一个链表的首结点，同时第一个链表的首结点的左指针链上第二个链表的尾结点。有木有读晕，可以自己画图，其实很好理解的诶

https://segmentfault.com/a/1190000016762566
https://www.geeksforgeeks.org/convert-a-binary-tree-to-a-circular-doubly-link-list/

    public Node treeToDoublyList(Node root) {
        if (root == null) return null;
        Node left = treeToDoublyList(root.left);
        Node right = treeToDoublyList(root.right);
        root.left = root;
        root.right = root;
        return join( join(left, root), right );
    }
    private Node join(Node left, Node right) {
        if (left == null) return right;
        if (right == null) return left;
        Node lastLeft = left.left;
        Node lastRight = right.left;
        
        lastLeft.right = right;
        right.left = lastLeft;
        lastRight.right = left;
        left.left = lastRight;
        
        return left;
    }

X. Stack

    Node* treeToDoublyList(Node* root) {
        if (!root) return NULL;
        Node *head = NULL, *pre = NULL;
        stack<Node*> st;
        while (root || !st.empty()) {
            while (root) {
                st.push(root);
                root = root->left;
            }
            root = st.top(); st.pop();
            if (!head) head = root;
            if (pre) {
                pre->right = root;
                root->left = pre;
            }
            pre = root;
            root = root->right;
        }
        head->left = pre;
        pre->right = head;
        return head;
    }

https://www.jianshu.com/p/584ce6519820?utm_campaign=maleskine&utm_content=note&utm_medium=seo_notes&utm_source=recommendation

1 因为要将一个binary search tree转换成一个有序的doubly linked list，因为是sorted的，所以其实就是binary search tree的inorder traversal
2 中序遍历有递归和迭代两种写法
3 双向链表有无环双向链表和有环双向链表两种，有可能会有follow up的问题
4 思路是每访问一个新的tree node，构建一个新的list node，一一对应上
5 因为是双向的，所以当建立一个新的list node后，我们需要建立与前后list node的连接，将新list node的previous pointer指向之前建立的list node，再将之前建立的list node的next pointer指向新建的这个list node
6 同时，我们需要记录一个state对象，state.pre记录之前的list node，state.head记录链表的头结点。但是怎么定义head呢，假如head之前没有节点了，也就是Null，就说明这是head，这是针对无环双向链表
7 由于是双向链表，所以最后，需要将首尾连接起来
8 建立 traverse函数，输入参数是node，返回基于这个node的tree建立的DLL的head和tail。所以使用递归函数后，traverse(root)，返回整个DLL的head和tail，然后把head和tail链接起来
9 返回head就是返回整个DLL
10 对于traverse函数，首先初始化head和tail为root。对于左子树和右子树，首先递归调用得到相应的head和tail，将root给tail.right，将tail给root.left，如果不存在左子树
11 对于traverse函数，如果输入node不存在左子树和右子树，则head和tail都是node自己；分左子树和右子树讨论后，对于左子树的情况，递归调用traverse函数，得到head和tail，这时将node给tail.right，同时将tail给node.left。同理，对于node.right，

You are supposed to play with pointers only. Assume left and right pointers of tree as previous and next pointers of doubly-linked list.

As we traverse the tree in-order, we can modify a node’s left pointer to point to its predecessor. We also have to modify the predecessor’s right pointer to point to the current node to maintain the doubly linked list behavior.

In this manner, we will be creating a list but that won’t be circular. We can solve this problem by creating a circular doubly linked list at every step in place of creating only doubly linked list. For this, we need to update the current node’s right pointer to point back to the head and the head’s left pointer to point to current node in each recursive call. As the recursion ends, the list’s head and tail would be automatically updated with the correct pointers.

i) an ordered binary tree (BST) storing numbers from 1 – 5.

// This is a modified in-order traversal adapted to this problem.

// prev (init to NULL) is used to keep track of previously traversed node.

// head pointer is updated with the list's head as recursion ends.

void treeToDoublyList(Node *p, Node *& prev, Node *& head) {

  if (!p) return;

  treeToDoublyList(p->left, prev, head);

  // current node's left points to previous node

  p->left = prev;

  if (prev)

    prev->right = p;  // previous node's right points to current node

  else

    head = p; // current node (smallest element) is head of

              // the list if previous node is not available

  // as soon as the recursion ends, the head's left pointer 

  // points to the last node, and the last node's right pointer

  // points to the head pointer.

  Node *right = p->right;

  head->left = p;

  p->right = head;

  // updates previous node

  prev = p;

  treeToDoublyList(right, prev, head);

}

// Given an ordered binary tree, returns a sorted circular

// doubly-linked list. The conversion is done in-place.

Node* treeToDoublyList(Node *root) {

  Node *prev = NULL;

  Node *head = NULL;

  treeToDoublyList(root, prev, head);

  return head;

}

The most important method is treeToList() and the helper methods join() and append(). Here are the lessons I see in the two solutions...

Trust that the recursive calls return correct output when fed correct input -- make the leap of faith. Look at the partial results that the recursive calls give you, and construct the full result from them. If you try to step into the recursive calls to think how they are working, you'll go crazy.
Decomposing out well defined helper functions is a good idea. Writing the list-append code separately helps you concentrate on the recursion which is complex enough on its own.

/*
helper function -- given two list nodes, join them
together so the second immediately follow the first.
Sets the .next of the first and the .previous of the second.
*/
public static void join(Node a, Node b) {
a.large = b;
b.small = a;
}

/*
helper function -- given two circular doubly linked
lists, append them and return the new list.
*/
public static Node append(Node a, Node b) {
// if either is null, return the other
if (a==null) return(b);
if (b==null) return(a);

// find the last node in each using the .previous pointer
Node aLast = a.small;
Node bLast = b.small;

// join the two together to make it connected and circular
join(aLast, b);
join(bLast, a);

return(a);
}
public static Node treeToList(Node root) {
// base case: empty tree -> empty list
if (root==null) return(null);

// Recursively do the subtrees (leap of faith!)
Node aList = treeToList(root.small);
Node bList = treeToList(root.large);

// Make the single root node into a list length-1
// in preparation for the appending
root.small = root;
root.large = root;

// At this point we have three lists, and it's
// just a matter of appending them together
// in the right order (aList, root, bList)
aList = append(aList, root);
aList = append(aList, bList);

return(aList);
}
http://sudhansu-codezone.blogspot.com/2012/01/binary-tree-to-circular-doubly-linked.html

EPI Solution: BSTToSortedDoublyList.java
public static BinaryTree<Integer> bstToDoublyLinkedList(
BinaryTree<Integer> n) {
// Empty subtree.
if (n == null) {
return null;
}

// Recursively build the list from left and right subtrees.
BinaryTree<Integer> lHead = bstToDoublyLinkedList(n.getLeft());
BinaryTree<Integer> rHead = bstToDoublyLinkedList(n.getRight());

// Append n to the list from left subtree.
BinaryTree<Integer> lTail = null;
if (lHead != null) {
lTail = lHead.getLeft();
lTail.setRight(n);
n.setLeft(lTail);
lTail = n;
} else {
lHead = lTail = n;
}

// Append the list from right subtree to n.
BinaryTree<Integer> rTail = null;
if (rHead != null) {
rTail = rHead.getLeft();
lTail.setRight(rHead);
rHead.setLeft(lTail);
} else {
rTail = lTail;
}
rTail.setRight(lHead);
lHead.setLeft(rTail);

return lHead;
}
http://coding-interview-archives.blogspot.com/2013/09/convert-given-binary-search-tree-into.html

Convert the left subtree recursively into DLL left_list.
Convert the right subtree recursively into DLL right_list.
Make the root's left and right point to itself thus making it a circular DLL of one node.
Merge root into left_list.
Merge right_list into left_list.
Return left_list.

Read full article from Convert Binary Search Tree (BST) to Sorted Doubly-Linked List | LeetCode

LeetCode 426 - Convert BST to Sorted Doubly Linked List

Labels

Popular Posts