LeetCode 699 - Falling Squares

https://leetcode.com/problems/falling-squares/solution/

On an infinite number line (x-axis), we drop given squares in the order they are given.

The i-th square dropped (positions[i] = (left, side_length)) is a square with the left-most point being positions[i][0]and sidelength positions[i][1].

The square is dropped with the bottom edge parallel to the number line, and from a higher height than all currently landed squares. We wait for each square to stick before dropping the next.

The squares are infinitely sticky on their bottom edge, and will remain fixed to any positive length surface they touch (either the number line or another square). Squares dropped adjacent to each other will not stick together prematurely.

Return a list ans of heights. Each height ans[i] represents the current highest height of any square we have dropped, after dropping squares represented by positions[0], positions[1], ..., positions[i].

Example 1:

Input: [[1, 2], [2, 3], [6, 1]]
Output: [2, 5, 5]
Explanation:

After the first drop of positions[0] = [1, 2]:
_aa
_aa
-------
The maximum height of any square is 2.


After the second drop of positions[1] = [2, 3]:
__aaa
__aaa
__aaa
_aa__
_aa__
--------------
The maximum height of any square is 5.  
The larger square stays on top of the smaller square despite where its center
of gravity is, because squares are infinitely sticky on their bottom edge.


After the third drop of positions[1] = [6, 1]:
__aaa
__aaa
__aaa
_aa
_aa___a
--------------
The maximum height of any square is still 5.

Thus, we return an answer of [2, 5, 5].

Example 2:

Input: [[100, 100], [200, 100]]
Output: [100, 100]
Explanation: Adjacent squares don't get stuck prematurely - only their bottom edge can stick to surfaces.

Note:

1 <= positions.length <= 1000.

1 <= positions[i][0] <= 10^8.

1 <= positions[i][1] <= 10^6.

Hint: If positions = [[10, 20], [20, 30]], this is the same as [[1, 2], [2, 3]]. Currently, the values of positions are very large. Can you generalize this approach so as to make the values in positions manageable?
https://leetcode.com/articles/falling-squares/
Intuitively, there are two operations: update, which updates our notion of the board (number line) after dropping a square; and query, which finds the largest height in the current board on some interval.

Coordinate Compression

In the below approaches, since there are only up to 2 * len(positions) critical points, namely the left and right edges of each square, we can use a technique called coordinate compression to map these critical points to adjacent integers

Set<Integer> coords = new HashSet();
for (int[] pos: positions) {
    coords.add(pos[0]);
    coords.add(pos[0] + pos[1] - 1);
}
List<Integer> sortedCoords = new ArrayList(coords);
Collections.sort(sortedCoords);

Map<Integer, Integer> index = new HashMap();
int t = 0;
for (int coord: sortedCoords) index.put(coord, t++);

Approach #4: Segment Tree with Lazy Propagation [Accepted]

If we were familiar with the idea of a segment tree (which supports queries and updates on intervals), we can immediately crack the problem.

Algorithm

Segment trees work by breaking intervals into a disjoint sum of component intervals, whose number is at most log(width). The motivation is that when we change an element, we only need to change log(width) many intervals that aggregate on an interval containing that element.

When we want to update an interval all at once, we need to use lazy propagation to ensure good run-time complexity. This topic is covered in more depth here.

With such an implementation in hand, the problem falls out immediately.

https://blog.csdn.net/u013007900/article/details/81065441
这种问题可以归结为，区间更新，区间查询。

如果是之前有一定竞赛基础的人就明显能感觉出来，这种东西要用线段树做。但是一看数据范围：L≤108L≤108。这就意味着至少需要2×1082×108的节点才能存下一棵线段树，会超过内存。

所以需要离散化，或者一些其他的写法进行优化。姿势有挺多的，我提供两种。

    class Node {
        public int l, r;
        public int max, value;
        public Node left, right;


        public Node(int l, int r, int max, int val) {
            this.l = l;
            this.r = r;
            this.max = max;
            this.value = val;
            this.right = null;
            this.left = null;
        }
    }

    private boolean intersect(Node n, int l, int r) {
        if (r <= n.l || l >= n.r) {
            return false;
        }
        return true;
    }

    private Node insert(Node root, int l, int r, int val) {
        if(root == null)
        {
            return new Node(l, r, r, val);
        }
        if(l <= root.l)
        {
            root.left = insert(root.left, l, r, val);
        }
        else
        {
            root.right = insert(root.right, l, r, val);
        }
        root.max = Math.max(r, root.max);
        return root;
    }

    private int query(Node root, int l, int r) {
        if(root == null || l >= root.max) {
            return 0;
        }

        int ans = 0;
        if(intersect(root, l, r)) {
            ans = root.value;
        }

        ans = Math.max(ans, query(root.left, l, r));

        if(r > root.l) {
            ans = Math.max(ans, query(root.right, l, r));
        }

        return ans;
    }

    public List<Integer> fallingSquares(int[][] positions) {
        List<Integer> ans = new ArrayList<>();
        Node root = null;
        int prev = 0;

        for (int i = 0; i < positions.length; i++) {
            int l = positions[i][0];
            int r = positions[i][0] + positions[i][1];
            int currentHeight = query(root, l, r);
            root = insert(root, l, r, currentHeight + positions[i][1]);
            prev = Math.max(prev, currentHeight + positions[i][1]);
            ans.add(prev);
        }
        return ans;
    }


https://leetcode.com/articles/a-recursive-approach-to-segment-trees-range-sum-queries-lazy-propagation/

https://leetcode.com/problems/falling-squares/discuss/112678/Treemap-solution-and-Segment-tree-(Java)-solution-with-lazy-propagation-and-coordinates-compression

    public List<Integer> fallingSquares(int[][] positions) {
        int n = positions.length;
        Map<Integer, Integer> cc = coorCompression(positions);
        int best = 0;
        List<Integer> res = new ArrayList<>();
        SegmentTree tree = new SegmentTree(cc.size());
        for (int[] pos : positions) {
            int L = cc.get(pos[0]);
            int R = cc.get(pos[0] + pos[1] - 1);
            int h = tree.query(L, R) + pos[1];
            tree.update(L, R, h);
            best = Math.max(best, h);
            res.add(best);
        }
        return res;
    }
    
    private Map<Integer, Integer> coorCompression(int[][] positions) {
        Set<Integer> set = new HashSet<>();
        for (int[] pos : positions) {
            set.add(pos[0]);
            set.add(pos[0] + pos[1] - 1);
        }
        List<Integer> list = new ArrayList<>(set);
        Collections.sort(list);
        Map<Integer, Integer> map = new HashMap<>();
        int t = 0;
        for (int pos : list) map.put(pos, t++);
        return map;
    }
    
    class SegmentTree {
        int[] tree;
        int N;
        
        SegmentTree(int N) {
            this.N = N;
            int n = (1 << ((int) Math.ceil(Math.log(N) / Math.log(2)) + 1));
            tree = new int[n];
        }
        
        public int query(int L, int R) {
            return queryUtil(1, 0, N - 1, L, R);
        }
        
        private int queryUtil(int index, int s, int e, int L, int R) {
            // out of range
            if (s > e || s > R || e < L) {
                return 0;
            }
            // [L, R] cover [s, e]
            if (s >= L && e <= R) {
                return tree[index];
            }
            // Overlapped
            int mid = s + (e - s) / 2;
            return Math.max(queryUtil(2 * index, s, mid, L, R), queryUtil(2 * index + 1, mid + 1, e, L, R));
        }
        
        public void update(int L, int R, int h) {
            updateUtil(1, 0, N - 1, L, R, h);
        }
        
        private void updateUtil(int index, int s, int e, int L, int R, int h) {
            // out of range
            if (s > e || s > R || e < L) {
                return;
            }
            tree[index] = Math.max(tree[index], h);
            if (s != e) {
                int mid = s + (e - s) / 2;
                updateUtil(2 * index, s, mid, L, R, h);
                updateUtil(2 * index + 1, mid + 1, e, L, R, h);
            }
        }
    }




Approach #3: Block (Square Root) Decomposition [Accepted]

Whenever we perform operations (like update and query) on some interval in a domain, we could segment that domain with size $W$ into blocks of size $\sqrt{W}$.

Then, instead of a typical brute force where we update our array heights representing the board, we will also hold another array blocks, where blocks[i] represents the $B = \lfloor \sqrt{W} \rfloor$ elements heights[B*i], heights[B*i + 1], ..., heights[B*i + B-1]. This allows us to write to the array in $O(B)$ operations.

Algorithm

Let's get into the details. We actually need another array, blocks_read. When we update some element iin block b = i / B, we'll also update blocks_read[b]. If later we want to read the entire block, we can read from here (and stuff written to the whole block in blocks[b].)

When we write to a block, we'll write in blocks[b]. Later, when we want to read from an element i in block b = i / B, we'll read from heights[i] and blocks[b].

Our process for managing query and update will be similar. While left isn't a multiple of B, we'll proceed with a brute-force-like approach, and similarly for right. At the end, [left, right+1) will represent a series of contiguous blocks: the interval will have length which is a multiple of B, and left will also be a multiple of B.

• Time Complexity: $O(N\sqrt{N})$, where $N$ is the length of positions. Each query and update has complexity $O(\sqrt{N})$.
• Space Complexity: $O(N)$, the space used by heights.

Approach #2: Brute Force with Coordinate Compression [Accepted]

Let N = len(positions). After mapping the board to a board of length at most $2* N \leq 2000$, we can brute force the answer by simulating each square's drop directly.

Our answer is either the current answer or the height of the square that was just dropped, and we'll update it appropriately.

• Time Complexity: $O(N^2)$, where $N$ is the length of positions. We use two for-loops, each of complexity $O(N)$ (because of coordinate compression.)
• Space Complexity: $O(N)$, the space used by heights.

    int[] heights;

    public int query(int L, int R) {
        int ans = 0;
        for (int i = L; i <= R; i++) {
            ans = Math.max(ans, heights[i]);
        }
        return ans;
    }

    public void update(int L, int R, int h) {
        for (int i = L; i <= R; i++) {
            heights[i] = Math.max(heights[i], h);
        }
    }

    public List<Integer> fallingSquares(int[][] positions) {
        //Coordinate Compression
        //HashMap<Integer, Integer> index = ...;
        //int t = ...;

        heights = new int[t];
        int best = 0;
        List<Integer> ans = new ArrayList();

        for (int[] pos: positions) {
            int L = index.get(pos[0]);
            int R = index.get(pos[0] + pos[1] - 1);
            int h = query(L, R) + pos[1];
            update(L, R, h);
            best = Math.max(best, h);
            ans.add(best);
        }
        return ans;
    }

Approach #1: Offline Propagation [Accepted]

Instead of asking the question "what squares affect this query?", lets ask the question "what queries are affected by this square?"

Let qans[i] be the maximum height of the interval specified by positions[i]. At the end, we'll return a running max of qans.

For each square positions[i], the maximum height will get higher by the size of the square we drop. Then, for any future squares that intersect the interval [left, right) (where left = positions[i][0], right = positions[i][0] + positions[i][1]), we'll update the maximum height of that interval.

• Time Complexity: $O(N^2)$, where $N$ is the length of positions. We use two for-loops, each of complexity $O(N)$.
• Space Complexity: $O(N)$, the space used by qans and ans.

    public List<Integer> fallingSquares(int[][] positions) {
        int[] qans = new int[positions.length];
        for (int i = 0; i < positions.length; i++) {
            int left = positions[i][0];
            int size = positions[i][1];
            int right = left + size;
            qans[i] += size;

            for (int j = i+1; j < positions.length; j++) {
                int left2 = positions[j][0];
                int size2 = positions[j][1];
                int right2 = left2 + size2;
                if (left2 < right && left < right2) { //intersect
                    qans[j] = Math.max(qans[j], qans[i]);
                }
            }
        }

        List<Integer> ans = new ArrayList();
        int cur = -1;
        for (int x: qans) {
            cur = Math.max(cur, x);
            ans.add(cur);
        }
        return ans;
    }

X. TreeMap
https://leetcode.com/problems/falling-squares/discuss/112678/Treemap-solution-and-Segment-tree-(Java)-solution-with-lazy-propagation-and-coordinates-compression
https://www.geeksforgeeks.org/lazy-propagation-in-segment-tree/

TreeMap Solution: The basic idea here is pretty simple, for each square i, I will find all the maximum height from previously dropped squares range from floorKey(i_start) (inclusive) to end (exclusive), then I will update the height and delete all the old heights.

    public List<Integer> fallingSquares(int[][] positions) {
        List<Integer> res = new ArrayList<>();
        TreeMap<Integer, Integer> startHeight = new TreeMap<>();
        startHeight.put(0, 0); 
        int max = 0;
        for (int[] pos : positions) {
            int start = pos[0], end = start + pos[1];
            Integer from = startHeight.floorKey(start);
            int height = startHeight.subMap(from, end).values().stream().max(Integer::compare).get() + pos[1];
            max = Math.max(height, max);
            res.add(max);
            // remove interval within [start, end)
            int lastHeight = startHeight.floorEntry(end).getValue();
            startHeight.put(start, height);
            startHeight.put(end, lastHeight);
            startHeight.keySet().removeAll(new HashSet<>(startHeight.subMap(start, false, end, false).keySet()));
        }
        return res;
    }

https://leetcode.com/problems/falling-squares/discuss/108775/Easy-Understood-TreeMap-Solution

The squares divide the number line into many segments with different heights. Therefore we can use a TreeMap to store the number line. The key is the starting point of each segment and the value is the height of the segment. For every new falling square (s, l), we update those segments between s and s + l.

    public List<Integer> fallingSquares(int[][] positions) {
        List<Integer> list = new ArrayList<>();
        TreeMap<Integer, Integer> map = new TreeMap<>();

        // at first, there is only one segment starting from 0 with height 0
        map.put(0, 0);
        
        // The global max height is 0
        int max = 0;

        for(int[] position : positions) {

            // the new segment 
            int start = position[0], end = start + position[1];

            // find the height among this range
            Integer key = map.floorKey(start);
            int h = map.get(key);
            key = map.higherKey(key);
            while(key != null && key < end) {
                h = Math.max(h, map.get(key));
                key = map.higherKey(key);
            }
            h += position[1];

            // update global max height
            max = Math.max(max, h);
            list.add(max);

            // update new segment and delete previous segments among the range
            int tail = map.floorEntry(end).getValue();
            map.put(start, h);
            map.put(end, tail);
            key = map.higherKey(start);
            while(key != null && key < end) {
                map.remove(key);
                key = map.higherKey(key);
            }
        }
        return list;
    }

https://leetcode.com/problems/falling-squares/discuss/108769/C++-O(nlogn)
Similar to skyline concept, going from left to right the path is decomposed to consecutive segments, and each segment has a height. Each time we drop a new square, then update the level map by erasing & creating some new segments with possibly new height. There are at most 2n segments that are created / removed throughout the process, and the time complexity for each add/remove operation is O(log(n)).
X. https://leetcode.com/problems/falling-squares/discuss/108766/Easy-Understood-O(n2)-Solution-with-explanation

The idea is quite simple, we use intervals to represent the square. the initial height we set to the square cur is pos[1]. That means we assume that all the square will fall down to the land. we iterate the previous squares, check is there any square i beneath my cur square. If we found that we have squares i intersect with us, which means my current square will go above to that square i. My target is to find the highest square and put square cur onto square i, and set the height of the square cur as

cur.height = cur.height + previousMaxHeight;

    private class Interval {
        int start, end, height;
        public Interval(int start, int end, int height) {
            this.start = start;
            this.end = end;
            this.height = height;
        }
    }
    public List<Integer> fallingSquares(int[][] positions) {
        List<Interval> intervals = new ArrayList<>();
        List<Integer> res = new ArrayList<>();
        int h = 0;
        for (int[] pos : positions) {
            Interval cur = new Interval(pos[0], pos[0] + pos[1] - 1, pos[1]);
            h = Math.max(h, getHeight(intervals, cur));
            res.add(h);
        }
        return res;
    }
    private int getHeight(List<Interval> intervals, Interval cur) {
        int preMaxHeight = 0;
        for (Interval i : intervals) {
            // Interval i does not intersect with cur
            if (i.end < cur.start) continue;
            if (i.start > cur.end) continue;
            // find the max height beneath cur
            preMaxHeight = Math.max(preMaxHeight, i.height);
        }
        cur.height += preMaxHeight;
        intervals.add(cur);
        return cur.height;
    }

https://blog.csdn.net/u014688145/article/details/78243313

有点几何题的味道，实际上正方形往上叠总共就5种情况，如下：

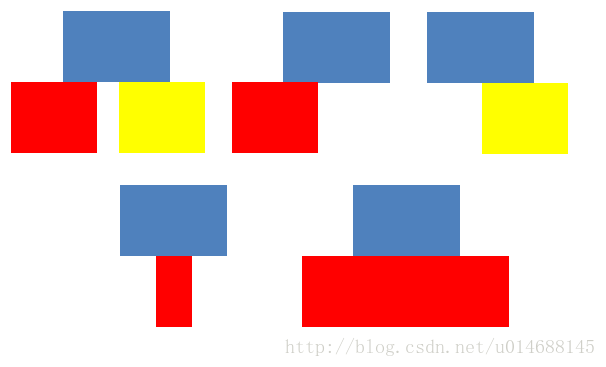
前四种情况，可以合并成一种情况处理，只需要搜索蓝色两条边界内是否存在对应的边，如果有，则说明需要叠加。第五种情况需要特殊处理，直接扫描所有正方形，包含蓝色矩形块则更新高度。

    public List<Integer> fallingSquares(int[][] positions) {
        int n = positions.length;
        List<Integer> ans = new ArrayList<>();

        TreeMap<Double, Integer> map = new TreeMap<>();
        List<Edge> heights = new ArrayList<Edge>();
        int max = 0;

        for (int i = 0; i < n; ++i) {
            int x = positions[i][0];
            int h = positions[i][1];
            int y = h + x - 1;


            int h_max = 0;
            for (Double e : map.subMap(x - 0.1, y + 0.1).keySet()) {
                h_max = Math.max(h_max, map.get(e));
            }

            for (Edge edge : heights) {
                if (edge.x <= x && edge.y >= y) {
                    h_max = Math.max(h_max, edge.h);
                }
            }

            h_max += h;

            map.put(x * 1.0, h_max);
            map.put(y * 1.0, h_max);
            heights.add(new Edge(x, y, h_max));

            max = Math.max(max, h_max);
            ans.add(max);
        }
        return ans;
    }       

public List<Integer> fallingSquares(int[][] positions) { int n = positions.length; List<Integer> ans = new ArrayList<>(); TreeMap<Double, Integer> map = new TreeMap<>(); for (int[] pos : positions) { int x = pos[0]; int h = pos[1]; int y = x + h - 1; map.put(x * 1.0, 0); map.put(y * 1.0, 0); } int max = 0; for (int i = 0; i < n; ++i) { int x = positions[i][0]; int h = positions[i][1]; int y = h + x - 1; int h_max = 0; for (Double e : map.subMap(x - 0.1, y + 0.1).keySet()) { h_max = Math.max(h_max, map.get(e)); } h_max += h; for (Double e : map.subMap(x - 0.1, y + 0.1).keySet()) { map.put(e, h_max); } max = Math.max(max, h_max); ans.add(max); } return ans; }
X. Interval Tree
https://leetcode.com/problems/falling-squares/discuss/108765/Java-14ms-beats-99.38-using-interval-tree

    class Node {
        public int l;
        public int r;
        public int max;
        public int height;
        public Node left;
        public Node right;
        
        public Node (int l, int r, int max, int height) {
            this.l = l;
            this.r = r;
            this.max = max;
            this.height = height;
        }
    }
    
    
    private boolean intersect(Node n, int l, int r) {
        if (r <= n.l || l >= n.r) {
            return false;
        }
        return true;
    }
    
    private Node insert(Node root, int l, int r, int height) {
        if (root == null) {
            return new Node(l, r, r, height);
        }
        
        if (l <= root.l) {
            root.left = insert(root.left, l, r, height);
        } else {
             // l > root.l
            root.right = insert(root.right, l, r, height);
        }
        root.max = Math.max(r, root.max);
        return root;
    }
    
    // return the max height for interval (l, r)
    private int maxHeight(Node root, int l, int r) {
        if (root == null || l >= root.max) {
            return 0;
        }
        
        int res = 0;
        if (intersect(root, l, r)) {
            res = root.height;
        }
        if (r > root.l) {
            res = Math.max(res, maxHeight(root.right, l, r));
        }
        res = Math.max(res, maxHeight(root.left, l, r));
        return res;
    }
    
    public List<Integer> fallingSquares(int[][] positions) {
        Node root = null;
        List<Integer> res = new ArrayList<>();
        int prev = 0;
        
        for (int i = 0; i < positions.length; ++i) {
            int l = positions[i][0];
            int r = positions[i][0] + positions[i][1];
            int currentHeight = maxHeight(root, l, r);
            root = insert(root, l, r, currentHeight + positions[i][1]);
            prev = Math.max(prev, currentHeight + positions[i][1]);
            res.add(prev);
        }
        
        return res;
    }

https://blog.csdn.net/u013007900/article/details/81065441
常规想法1
发现NN非常小，所以从NN着手考虑。

对于每一次新落下的方块，当前方块的高度等于，所有之前落下的并和它有重叠部分的最高高度，加上当前落下方块的高度。

假设当前处理到了ii，我们从ii往00扫描，找到和他有重叠的最高高度，就是这个方块的高度，我们将这个值记录为height[i]height[i]。

最终答案显而易见的就是对heightheight数组做一次取前缀最大值。

时间复杂度为O(N2)O(N2)。

多考虑一下就会发现，这种重叠部分可以被当做一个个区间。一个区间内的高度是一致的，所以我们只需要去维护一个个区间就能知道当前方块的高度。

这里可以估算一下区间的个数，不超过2×N2×N，所以也可以用上面那种O(N2)O(N2)的方式去解决。

假设处理到了ii，我们扫描区间数列找到所有重合的区间，除开头尾可能没有完全覆盖的区间要进行拆分，其他的区间都要更新为重合区间中的最大值加上S[i]S[i]的数。（关于这儿对于完全覆盖区间的处理，可以选择删除，也可以选择留着然后仍然维护，区别不大）

常规想法3
上面的想法是扫描区间数列得到重合的区间，如果维护区间数列的时候，是按照顺序来的排列的，则可以进行两次二分查找，找到上下界即可。