http://bookshadow.com/weblog/2017/11/05/leetcode-candy-crush/
这道题目本身并不难,算法框架分为两步:1)标记出所有需要被crash掉的元素;2)将这些元素置为0,并且crash。但是我感觉难的地方是如何确定哪些元素需要被crash。例如在题目中给出的例子中,5个“2”需要被crash,但是只有4个“1”需要被crash,而board[8][0]位置上的1不可以被crash(这也是我开始写的程序怎么都跑不对的原因)。为了解决这一问题,我的思路是:如果一个元素可以被crash,则我们首先将其置为负数。这样在判断某个元素是否可以被crash的时候,我们就判断它的纵向或者横向是否存在三个连续的位置,其值不为0,并且绝对值相同。如果可以被crash,则将其置为原数对应的负数。这样在后面crash的时候,我们只需要保留正数,而将所有的非正数都置为0。
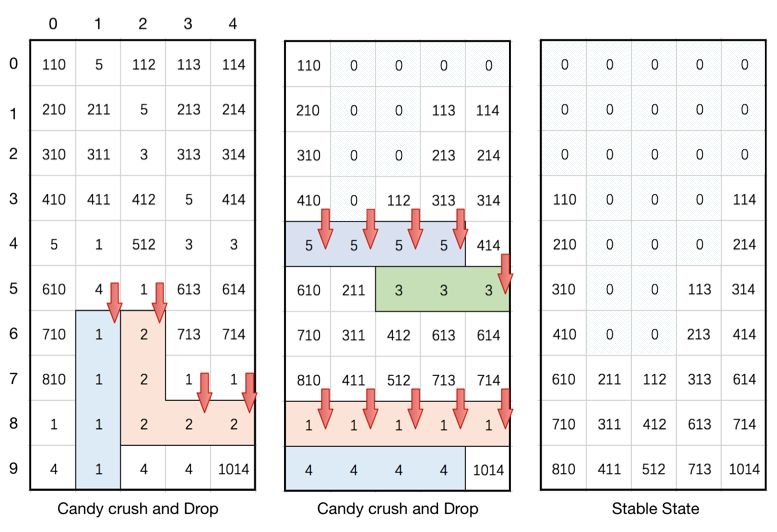
这道题就是糖果消消乐,博主刚开始做的时候,没有看清楚题意,以为就像游戏中的那样,每次只能点击一个地方,然后消除后糖果落下,这样会导致一个问题,就是原本其他可以消除的地方在糖果落下后可能就没有了,所以博主在想点击的顺序肯定会影响最终的stable的状态,可是题目怎么没有要求返回所剩糖果最少的状态?后来发现,其实这道题一次消除table中所有可消除的糖果,然后才下落,形成新的table,这样消除后得到的结果就是统一的了,这样也大大的降低了难度。下面就来看如何找到要消除的糖果,可能有人会想像之前的岛屿的题目一样找连通区域,可是这道题的有限制条件,只有横向或竖向相同的糖果数达到三个才能消除,并不是所有的连通区域都能消除,所以找连通区域不是一个好办法。最好的办法其实是每个糖果单独检查其是否能被消除,然后把所有能被删除的糖果都标记出来统一删除,然后在下落糖果,然后再次查找,直到无法找出能够消除的糖果时达到稳定状态。好,那么我们用一个数组来保存可以被消除的糖果的位置坐标,判断某个位置上的糖果能否被消除的方法就是检查其横向和纵向的最大相同糖果的个数,只要有一个方向达到三个了,当前糖果就可以被消除。所以我们对当前糖果的上下左右四个方向进行查看,用四个变量x0, x1, y0, y1,其中x0表示上方相同的糖果的最大位置,x1表示下方相同糖果的最大位置,y0表示左边相同糖果的最大位置,y1表示右边相同糖果的最大位置,均初始化为当前糖果的位置,然后使用while循环向每个方向遍历,注意我们并不需要遍历到头,而是只要遍历三个糖果就行了,因为一旦查到了三个相同的,就说明当前的糖果已经可以消除了,没必要再往下查了。查的过程还要注意处理越界情况,好,我们得到了上下左右的最大的位置,分别让相同方向的做差,如果水平和竖直方向任意一个大于3了,就说明可以消除,将坐标加入数组del中。注意这里一定要大于3,是因为当发现不相等退出while循环时,坐标值已经改变了,所以已经多加了或者减了一个,所以差值要大于3。遍历完成后,如果数组del为空,说明已经stable了,直接break掉,否则将要消除的糖果位置都标记为0,然后进行下落处理。下落处理实际上是把数组中的0都移动到开头,那么就从数组的末尾开始遍历,用一个变量t先指向末尾,然后然后当遇到非0的数,就将其和t位置上的数置换,然后t自减1,这样t一路减下来都是非0的数,而0都被置换到数组开头了
画图模拟比较好理解.
vector<vector<int>> candyCrush(vector<vector<int>>& board) { int m = board.size(); int n = board[0].size(); while (true) { vector<pair<int, int>> to_crash; for (int i = 0; i < m; i++) { for (int j = 0; j < n; j++) { if (board[i][j]) { //为了减小计算量,元素为0的略过 int i1 = i, i0 = i, j1 = j, j0 = j; // i1,i0,j1,j0分别为向下,向上,向右,向左的检测 //对每个点(i,j),以其为中心,向上下或左右方向扩展,看是否有连续 while (i1 < m && i1 < i+3 && board[i1][j] == board[i][j]) i1++; while (i0 >= 0 && i0 > i-3 && board[i0][j] == board[i][j]) i0--; while (j1 < n && j1 < j+3 && board[i][j1] == board[i][j]) j1++; while (j0 >= 0 && j0 > j-3 && board[i][j0] == board[i][j]) j0--; if (i1-i0 > 3 || j1-j0 > 3) to_crash.push_back({i,j}); //上下或左右连续元素超过3,即符合 } } } if (to_crash.empty()) break; for (auto t : to_crash) board[t.first][t.second] = 0; //重点:将所有标记位置置0 for (int j = 0; j < n; j++) { //由于是自上往下消除,因此外层对j(纵坐标)循环 int t = m-1; //t用于记录新board的横坐标 for (int i = m-1; i >= 0; i--) { //从下往上,非0元素参与交换,每次交换后t上移 if (board[i][j]) swap(board[i][j], board[t--][j]); } } } return board; }
https://www.cnblogs.com/jxr041100/p/8440349.html
X. http://storypku.com/2017/11/leetcode-question-723-candy-crush/
This question is about implementing a basic elimination algorithm for Candy Crush.
Given a 2D integer array
board representing the grid of candy, different positive integers board[i][j]represent different types of candies. A value of board[i][j] = 0 represents that the cell at position (i, j) is empty. The given board represents the state of the game following the player's move. Now, you need to restore the board to a stable state by crushing candies according to the following rules:- If three or more candies of the same type are adjacent vertically or horizontally, "crush" them all at the same time - these positions become empty.
- After crushing all candies simultaneously, if an empty space on the board has candies on top of itself, then these candies will drop until they hit a candy or bottom at the same time. (No new candies will drop outside the top boundary.)
- After the above steps, there may exist more candies that can be crushed. If so, you need to repeat the above steps.
- If there does not exist more candies that can be crushed (ie. the board is stable), then return the current board.
You need to perform the above rules until the board becomes stable, then return the current board.
Example 1:
Note:
- The length of
boardwill be in the range [3, 50]. - The length of
board[i]will be in the range [3, 50]. - Each
board[i][j]will initially start as an integer in the range [1, 2000].
模拟实现游戏“糖果粉碎传奇”
给定二维数组board,每行、列中3个或以上连续相同的数字都可以被消去(变为0表示空位),消去后位于上方的数字会填充空位。
重复直到没有更多的数字可以被消去。
https://blog.csdn.net/magicbean2/article/details/79331607这道题目本身并不难,算法框架分为两步:1)标记出所有需要被crash掉的元素;2)将这些元素置为0,并且crash。但是我感觉难的地方是如何确定哪些元素需要被crash。例如在题目中给出的例子中,5个“2”需要被crash,但是只有4个“1”需要被crash,而board[8][0]位置上的1不可以被crash(这也是我开始写的程序怎么都跑不对的原因)。为了解决这一问题,我的思路是:如果一个元素可以被crash,则我们首先将其置为负数。这样在判断某个元素是否可以被crash的时候,我们就判断它的纵向或者横向是否存在三个连续的位置,其值不为0,并且绝对值相同。如果可以被crash,则将其置为原数对应的负数。这样在后面crash的时候,我们只需要保留正数,而将所有的非正数都置为0。
模拟题
循环,把拟被消去的数字替换为其相反数,遍历每一列,自底向上遍历每一行,将负数消去。
当某一次消去未找到任何数字时,循环终止。
https://github.com/joy32812/leetcode/blob/master/src/com/leetcode/P723_CandyCrush.java
int m, n;
int[][] B;
public int[][] candyCrush(int[][] board) {
B = board;
m = B.length;
n = B[0].length;
while (crash()) {
drop();
}
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
System.out.print(B[i][j] + " ");
}
System.out.println();
}
return B;
}
private boolean crash() {
boolean[][] c = new boolean[m][n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (B[i][j] == 0)
continue;
int cnt = 1;
// right
for (int k = j + 1; k < n; k++) {
if (B[i][k] == B[i][j])
cnt++;
else
break;
}
if (cnt >= 3) {
for (int k = j; k < n && k < j + cnt; k++) {
c[i][k] = true;
}
}
// down
cnt = 1;
for (int k = i + 1; k < m; k++) {
if (B[i][j] == B[k][j])
cnt++;
else
break;
}
if (cnt >= 3) {
for (int k = i; k < m && k < i + cnt; k++) {
c[k][j] = true;
}
}
}
}
boolean crash = false;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (c[i][j]) {
crash = true;
B[i][j] = 0;
}
}
}
return crash;
}
private void drop() {
for (int j = 0; j < n; j++) {
int now = m - 1;
for (int i = m - 1; i >= 0; i--) {
if (B[i][j] == 0)
continue;
int tp = B[i][j];
B[i][j] = B[now][j];
B[now][j] = tp;
now--;
}
}
}
http://www.cnblogs.com/grandyang/p/7858414.html这道题就是糖果消消乐,博主刚开始做的时候,没有看清楚题意,以为就像游戏中的那样,每次只能点击一个地方,然后消除后糖果落下,这样会导致一个问题,就是原本其他可以消除的地方在糖果落下后可能就没有了,所以博主在想点击的顺序肯定会影响最终的stable的状态,可是题目怎么没有要求返回所剩糖果最少的状态?后来发现,其实这道题一次消除table中所有可消除的糖果,然后才下落,形成新的table,这样消除后得到的结果就是统一的了,这样也大大的降低了难度。下面就来看如何找到要消除的糖果,可能有人会想像之前的岛屿的题目一样找连通区域,可是这道题的有限制条件,只有横向或竖向相同的糖果数达到三个才能消除,并不是所有的连通区域都能消除,所以找连通区域不是一个好办法。最好的办法其实是每个糖果单独检查其是否能被消除,然后把所有能被删除的糖果都标记出来统一删除,然后在下落糖果,然后再次查找,直到无法找出能够消除的糖果时达到稳定状态。好,那么我们用一个数组来保存可以被消除的糖果的位置坐标,判断某个位置上的糖果能否被消除的方法就是检查其横向和纵向的最大相同糖果的个数,只要有一个方向达到三个了,当前糖果就可以被消除。所以我们对当前糖果的上下左右四个方向进行查看,用四个变量x0, x1, y0, y1,其中x0表示上方相同的糖果的最大位置,x1表示下方相同糖果的最大位置,y0表示左边相同糖果的最大位置,y1表示右边相同糖果的最大位置,均初始化为当前糖果的位置,然后使用while循环向每个方向遍历,注意我们并不需要遍历到头,而是只要遍历三个糖果就行了,因为一旦查到了三个相同的,就说明当前的糖果已经可以消除了,没必要再往下查了。查的过程还要注意处理越界情况,好,我们得到了上下左右的最大的位置,分别让相同方向的做差,如果水平和竖直方向任意一个大于3了,就说明可以消除,将坐标加入数组del中。注意这里一定要大于3,是因为当发现不相等退出while循环时,坐标值已经改变了,所以已经多加了或者减了一个,所以差值要大于3。遍历完成后,如果数组del为空,说明已经stable了,直接break掉,否则将要消除的糖果位置都标记为0,然后进行下落处理。下落处理实际上是把数组中的0都移动到开头,那么就从数组的末尾开始遍历,用一个变量t先指向末尾,然后然后当遇到非0的数,就将其和t位置上的数置换,然后t自减1,这样t一路减下来都是非0的数,而0都被置换到数组开头了
vector<vector<int>> candyCrush(vector<vector<int>>& board) { int m = board.size(), n = board[0].size(); while (true) { vector<pair<int, int>> del; for (int i = 0; i < m; ++i) { for (int j = 0; j < n; ++j) { if (board[i][j] == 0) continue; int x0 = i, x1 = i, y0 = j, y1 = j; while (x0 >= 0 && x0 > i - 3 && board[x0][j] == board[i][j]) --x0; while (x1 < m && x1 < i + 3 && board[x1][j] == board[i][j]) ++x1; while (y0 >= 0 && y0 > j - 3 && board[i][y0] == board[i][j]) --y0; while (y1 < n && y1 < j + 3 && board[i][y1] == board[i][j]) ++y1; if (x1 - x0 > 3 || y1 - y0 > 3) del.push_back({i, j}); } } if (del.empty()) break; for (auto a : del) board[a.first][a.second] = 0; for (int j = 0; j < n; ++j) { int t = m - 1; for (int i = m - 1; i >= 0; --i) { if (board[i][j]) swap(board[t--][j], board[i][j]); } } } return board; }https://www.codetd.com/article/154114
画图模拟比较好理解.
vector<vector<int>> candyCrush(vector<vector<int>>& board) { int m = board.size(); int n = board[0].size(); while (true) { vector<pair<int, int>> to_crash; for (int i = 0; i < m; i++) { for (int j = 0; j < n; j++) { if (board[i][j]) { //为了减小计算量,元素为0的略过 int i1 = i, i0 = i, j1 = j, j0 = j; // i1,i0,j1,j0分别为向下,向上,向右,向左的检测 //对每个点(i,j),以其为中心,向上下或左右方向扩展,看是否有连续 while (i1 < m && i1 < i+3 && board[i1][j] == board[i][j]) i1++; while (i0 >= 0 && i0 > i-3 && board[i0][j] == board[i][j]) i0--; while (j1 < n && j1 < j+3 && board[i][j1] == board[i][j]) j1++; while (j0 >= 0 && j0 > j-3 && board[i][j0] == board[i][j]) j0--; if (i1-i0 > 3 || j1-j0 > 3) to_crash.push_back({i,j}); //上下或左右连续元素超过3,即符合 } } } if (to_crash.empty()) break; for (auto t : to_crash) board[t.first][t.second] = 0; //重点:将所有标记位置置0 for (int j = 0; j < n; j++) { //由于是自上往下消除,因此外层对j(纵坐标)循环 int t = m-1; //t用于记录新board的横坐标 for (int i = m-1; i >= 0; i--) { //从下往上,非0元素参与交换,每次交换后t上移 if (board[i][j]) swap(board[i][j], board[t--][j]); } } } return board; }
https://www.cnblogs.com/jxr041100/p/8440349.html
public int[][] candyCrush(int[][] board) { if (board == null || board.length == 0 || board[0].length == 0) return board; int cnt = 0; int m = board.length, n = board[0].length; for (int i = 0; i < m; i++) { for (int j = 0; j < n; j++) { if (board[i][j] == 0) continue; if ( (i > 0 && Math.abs(board[i-1][j]) == board[i][j] && (i < m - 1 && board[i+1][j] == board[i][j])) || (i > 1 && Math.abs(board[i-1][j]) == board[i][j] && Math.abs(board[i-2][j]) == board[i][j]) || (i < m - 2 && board[i+1][j] == board[i][j] && board[i+2][j] == board[i][j]) || (j > 0 && Math.abs(board[i][j-1]) == board[i][j] && (j < n - 1 && board[i][j+1] == board[i][j])) || (j > 1 && Math.abs(board[i][j-1]) == board[i][j] && Math.abs(board[i][j-2]) == board[i][j]) || (j < n - 2 && board[i][j+1] == board[i][j] && board[i][j+2] == board[i][j])) { cnt++; board[i][j] = -board[i][j]; } } } for (int j = 0; j < n; j++) { int ptr = m - 1; for (int i = m - 1; i >= 0; i--) { if (board[i][j] > 0) { board[ptr--][j] = board[i][j]; } } for (int i = ptr; i >= 0; i--) { board[i][j] = 0; } } if (cnt == 0) { return board; } else { return candyCrush(board); } }https://www.cnblogs.com/lightwindy/p/9744174.html
vector<vector<int>> candyCrush(vector<vector<int>>& board) { const auto R = board.size(), C = board[0].size(); bool changed = true; while (changed) { changed = false; for (int r = 0; r < R; ++r) { for (int c = 0; c + 2 < C; ++c) { auto v = abs(board[r][c]); if (v != 0 && v == abs(board[r][c + 1]) && v == abs(board[r][c + 2])) { board[r][c] = board[r][c + 1] = board[r][c + 2] = -v; changed = true; } } } for (int r = 0; r + 2 < R; ++r) { for (int c = 0; c < C; ++c) { auto v = abs(board[r][c]); if (v != 0 && v == abs(board[r + 1][c]) && v == abs(board[r + 2][c])) { board[r][c] = board[r + 1][c] = board[r + 2][c] = -v; changed = true; } } } for (int c = 0; c < C; ++c) { int empty_r = R - 1; for (int r = R - 1; r >= 0; --r) { if (board[r][c] > 0) { board[empty_r--][c] = board[r][c]; } } for (int r = empty_r; r >= 0; --r) { board[r][c] = 0; } } } return board; }
X. http://storypku.com/2017/11/leetcode-question-723-candy-crush/
vector<vector<int>> candyCrush(vector<vector<int>>& board) {
int m = board.size(), n = board[0].size();
bool toBeContinued = false;
for (int i = 0; i < m; ++i) { // horizontal crushing
for (int j = 0; j + 2 < n; ++j) {
int& v1 = board[i][j];
int& v2 = board[i][j+1];
int& v3 = board[i][j+2];
int v0 = std::abs(v1);
if (v0 && v0 == std::abs(v2) && v0 == std::abs(v3)) {
v1 = v2 = v3 = - v0;
toBeContinued = true;
}
}
}
for (int i = 0; i + 2 < m; ++i) { // vertical crushing
for (int j = 0; j < n; ++j) {
int& v1 = board[i][j];
int& v2 = board[i+1][j];
int& v3 = board[i+2][j];
int v0 = std::abs(v1);
if (v0 && v0 == std::abs(v2) && v0 == std::abs(v3)) {
v1 = v2 = v3 = -v0;
toBeContinued = true;
}
}
}
for (int j = 0; j < n; ++j) { // gravity step
int dropTo = m - 1;
for (int i = m - 1; i >= 0; --i) {
if (board[i][j] >= 0) {
board[dropTo--][j] = board[i][j];
}
}
for (int i = dropTo; i >= 0; i--) {
board[i][j] = 0;
}
}
return toBeContinued ? candyCrush(board) : board;
}