LeetCode 688 - Knight Probability in Chessboard

https://leetcode.com/problems/knight-probability-in-chessboard/

On an NxN chessboard, a knight starts at the r-th row and c-th column and attempts to make exactly K moves. The rows and columns are 0 indexed, so the top-left square is (0, 0), and the bottom-right square is (N-1, N-1).

A chess knight has 8 possible moves it can make, as illustrated below. Each move is two squares in a cardinal direction, then one square in an orthogonal direction.

Each time the knight is to move, it chooses one of eight possible moves uniformly at random (even if the piece would go off the chessboard) and moves there.

The knight continues moving until it has made exactly K moves or has moved off the chessboard. Return the probability that the knight remains on the board after it has stopped moving.

Example:

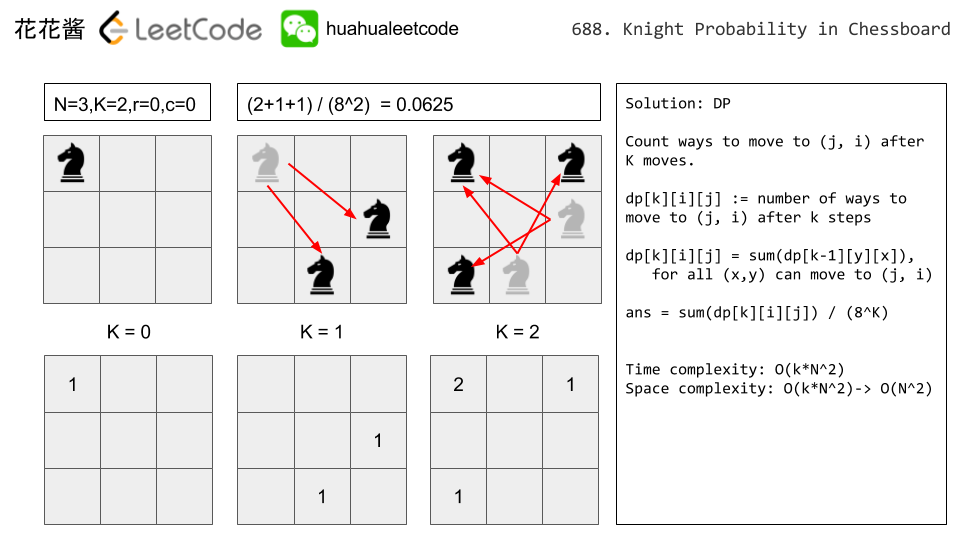
Input: 3, 2, 0, 0
Output: 0.0625
Explanation: There are two moves (to (1,2), (2,1)) that will keep the knight on the board.
From each of those positions, there are also two moves that will keep the knight on the board.
The total probability the knight stays on the board is 0.0625.

Note:

N will be between 1 and 25.

K will be between 0 and 100.

The knight always initially starts on the board.

X.
https://zxi.mytechroad.com/blog/dynamic-programming/688-knight-probability-in-chessboard/

Time Complexity: O(k*n^2)

Space Complexity: O(n^2)

https://github.com/cherryljr/LeetCode/blob/master/Knight%20Probability%20in%20Chessboard.java

 * 至此我们已经写出了 记忆化搜索 的方法了...其实已经写出 DP 的方法了。
 * 不过在最后，还是带着大家分析一遍直接从 DP 入手的话该怎么做吧。
 * 我们发现这是一个 无后效性 问题，当 位置 和 剩余步数 这两个信息确定之后，
 * 走完所有步数并且还留在棋盘上的方案数（结果）就已经确定了，与如何到达该位置并无关系。
 * 因此我们可以将原来的 DFS 方法改为 DP 方法。
 * dp[i][j][step] 代表骑士当前在 [i, j] 的位置，走Step步留在棋盘上的方案数。
 * 经过 以上分析（好吧，其实也没分析什么...）我们可以知道当前位置的信息 dp[i][j] 依赖于：
 * dp[i + dir[0]][j + dir[1]][step - 1] 这 8 个位置的信息。（如果有效的话）
 * 最终结果为：dp[r][c][step]
 * 对此我们需要对 dp[][] 进行一个初始化，当 step == 0 时，则 dp[i][j] = 1.
 * 因为这里的位置信息只依赖于 上一步 的信息。这就意味着原本的 三维矩阵 中的 Step 这一维的空间其实可以被优化掉。
 * 即我们使用 两个 二维矩阵的空间就够了(实际上就是一个滚动数组)。
 *
 * 时间复杂度：O(N^2*K)
 * 空间复杂度：O(N^2)
 */
class Solution {
    public double knightProbability(int N, int K, int r, int c) {
        double[][] dp = new double[N][N];
        // Initialize
        for (double[] row : dp) {
            Arrays.fill(row, 1);
        }
        int[][] dirs = new int[][]{{-1, -2}, {-2,  -1}, {-2, 1}, {-1, 2}, {1, -2}, {2, -1}, {2, 1}, {1, 2}};

        for (int k = 0; k < K; k++) {
            // Create the temp dp[][] to store message.
            double[][] dp2 = new double[N][N];
            for (int i = 0; i < N; i++) {
                for (int j = 0; j < N; j++) {
                    for (int[] dir : dirs) {
                        int nextRow = i + dir[0];
                        int nextCol = j + dir[1];
                        if (isOnBoard(nextRow, nextCol, N)) {
                            dp2[i][j] += dp[nextRow][nextCol];
                        }
                    }
                }
            }
            // Update the dp[][] message.
            dp = dp2;
        }

        return dp[r][c] / Math.pow(8, K);
    }

    private boolean isOnBoard(int row, int col, int N) {
        if (row < 0 || row >= N || col < 0 || col >= N) {
            return false;
        }
        return true;
    }

https://blog.csdn.net/XX_123_1_RJ/article/details/81149267
令 f[r][c][steps]表示， 经过steps步之后落在棋盘(r, c) 上的概率。则dp递推方程如下：
f[r][c][steps]=∑dr,dcf[ri+dr][cj+dc][steps−1]/8
f[r][c][steps]=∑dr,dcf[ri+dr][cj+dc][steps−1]/8

dr, dc 表示下一步要走的偏量，且r = ri+dr，c = cj+dc，也就是，只要在steps-1的步骤中，所有可能的位置到达steps步骤中的(r, c)，的概率总和，就是steps步骤中(r, c)的概率。最后只要求出在最后一步棋盘上所有位置上概率的总和就是题目要求的结果。
问题：为什么要除以8？因为每次有八分之一的概率选择一个方向，也就是每个位置被选择的概率是1/8。
问题：出界的概率怎么办？这个不用考虑，因为，只求界内的概率，所以不用考虑出界的概率。
现在看看优化问题，很显然，在每一个steps步骤中，只需要当前步骤steps的数据，和前一个steps-1的数据，就可以完成计算，所以f[r][c][steps] 这个3维数组，完全可以用两个2维数组代替。
所以用，dp2表示 f[][][steps]，用dp表示f[][][steps-1]。

    def knightProbability(self, N, K, r, c):
        dp = [[0] * N for _ in range(N)]  # 初始化dp
        dp[r][c] = 1
        for _ in range(K):
            dp2 = [[0] * N for _ in range(N)]  # 初始化当前dp
            for r in range(N):
                for c in range(N):
                    for dr, dc in zip((2, 2, -2, -2, 1, 1, -1, -1), (1, -1, 1, -1, 2, -2, 2, -2)):  # 八个方向
                        if 0 <= r + dr < N and 0 <= c + dc < N:  # 判断是否出界
                            dp2[r+dr][c+dc] += dp[r][c] / 8.0  # 保留棋盘内的概率（除以8，是因为有八个方向，每个方向是八分之一）
            dp = dp2  # 更新steps-1步骤中的棋盘概率数据
        return sum(map(sum, dp))  # 把落在棋盘上的所有位置的概率加起来，就是最后落在棋盘上的概率
http://www.ciaoshen.com/algorithm/leetcode/2018/12/05/leetcode-knight-probability-in-chessboard.html

    private int size;
    private double[][] oldBoard, newBoard;

    private void init(int size) {
        this.size = size;
        oldBoard = new double[size][size];
        newBoard = new double[size][size];
    }
    public double knightProbability(int N, int K, int r, int c) {
        if (K == 0) return 1.0;
        init(N);
        for (int i = 0; i < N; i++) Arrays.fill(oldBoard[i], 1.0);
        for (int i = 0; i < K - 1; i++) {
            for (int j = 0; j < N; j++) {
                for (int k = 0; k < N; k++) {
                    newBoard[j][k] = sumProb(j, k, oldBoard);
                }
            }
            double[][] temp = oldBoard;
            oldBoard = newBoard;
            newBoard = temp;
        }
        return sumProb(r, c, oldBoard);
    }

    private double sumProb(int r, int c, double[][] board) {
        double sum = 0;
        sum  += (onTheBoard(r + 1, c + 2))? board[r + 1][c + 2] : 0;
        sum  += (onTheBoard(r + 2, c + 1))? board[r + 2][c + 1] : 0;
        sum  += (onTheBoard(r + 2, c - 1))? board[r + 2][c - 1] : 0;
        sum  += (onTheBoard(r + 1, c - 2))? board[r + 1][c - 2] : 0;
        sum  += (onTheBoard(r - 1, c - 2))? board[r - 1][c - 2] : 0;
        sum  += (onTheBoard(r - 2, c - 1))? board[r - 2][c - 1] : 0;
        sum  += (onTheBoard(r - 2, c + 1))? board[r - 2][c + 1] : 0;
        sum  += (onTheBoard(r - 1, c + 2))? board[r - 1][c + 2] : 0;
        return sum / 8;
    }

    private boolean onTheBoard(int r, int c) {
        return r >= 0 && r < size && c >= 0 && c < size;
    }

https://leetcode.com/problems/knight-probability-in-chessboard/solution/

Let f[r][c][steps] be the probability of being on square (r, c) after steps steps. Based on how a knight moves, we have the following recursion:

$f[r][c][steps] = \sum_{dr, dc} f[r+dr][c+dc][steps-1] / 8.0$

where the sum is taken over the eight $(dr, dc)$ pairs $(2, 1),$ $(2, -1),$ $(-2, 1),$ $(-2, -1),$ $(1, 2),$ $(1, -2),$ $(-1, 2),$ $(-1, -2)$.

Instead of using a three-dimensional array f, we will use two two-dimensional ones dp and dp2, storing the result of the two most recent layers we are working on. dp2 will represent f[][][steps], and dp will represent f[][][steps-1].

• Time Complexity: $O(N^2 K)$ where $N, K$ are defined as in the problem. We do $O(1)$ work on each layer dp of $N^2$ elements, and there are $K$ layers considered.
• Space Complexity: $O(N^2)$, the size of dp and dp2.

https://leetcode.com/problems/knight-probability-in-chessboard/discuss/108181/My-accepted-DP-solution

It's no need to create 'double[][] dp1' inside the loop. Create it outside and reuse it, swap 'dp0' and 'dp1' after calculating.

    public double knightProbability(int N, int K, int sr, int sc) {

        double[][] dp = new double[N][N];

        int[] dr = new int[]{2, 2, 1, 1, -1, -1, -2, -2};

        int[] dc = new int[]{1, -1, 2, -2, 2, -2, 1, -1};

        dp[sr][sc] = 1;

        for (; K > 0; K--) {

            double[][] dp2 = new double[N][N];

            for (int r = 0; r < N; r++) {

                for (int c = 0; c < N; c++) {

                    for (int k = 0; k < 8; k++) {

                        int cr = r + dr[k];

                        int cc = c + dc[k];

                        if (0 <= cr && cr < N && 0 <= cc && cc < N) {

                            dp2[cr][cc] += dp[r][c] / 8.0;

                        }

                    }

                }

            }

            dp = dp2;

        }

        double ans = 0.0;

        for (double[] row: dp) {

            for (double x: row) ans += x;

        }

        return ans;

    }

https://leetcode.com/problems/knight-probability-in-chessboard/discuss/108214/My-easy-understand-dp-solution

    private int[][] dirs = new int[][]{{1, 2}, {2, 1}, {2, -1}, {1, -2}, {-1, -2}, {-2, -1}, {-2, 1}, {-1, 2}};
    public double knightProbability(int N, int K, int r, int c) {
        double[][][] dp = new double[K + 1][N][N];
        dp[0][r][c] = 1;
        for (int step = 1; step <= K; step++) {
            for (int i = 0; i < N; i++) {
                for (int j = 0; j < N; j++) {
                    for (int[] dir : dirs) {
                        int x = dir[0] + i;
                        int y = dir[1] + j;
                        if (x < 0 || x >= N || y < 0 || y >= N) continue;
                        dp[step][i][j] += dp[step - 1][x][y] * 0.125;
                    }
                }
            }
        }
        double res = 0;
        for (int i = 0; i < N; i++) {
            for (int j = 0; j < N; j++) {
                res += dp[K][i][j];
            }
        }
        return res;
    }

X.  http://www.cnblogs.com/grandyang/p/7639153.html

这道题给了我们一个大小为NxN国际象棋棋盘，上面有个骑士，相当于我们中国象棋中的马，能走‘日’字，给了我们一个起始位置，然后说允许我们走K步，问走完K步之后还能留在棋盘上的概率是多少。那么要求概率，我们必须要先分别求出分子和分母，其中分子是走完K步还在棋盘上的走法，分母是没有限制条件的总共的走法。那么分母最好算，每步走有8种跳法，那么K步就是8的K次方种了。关键是要求出分子，博主开始向的方法是以给定位置为起始点，然后进行BFS，每步遍历8种情况，遇到在棋盘上的就计数器加1，结果TLE了。上论坛看大家的解法，结果发现都是换了一个角度来解决问题的，并不很关心骑士的起始位置，而是把棋盘上所有位置上经过K步还留在棋盘上的走法总和都算出来，那么最后直接返回需要的值即可。跟之前那道Out of Boundary Paths没啥本质上的区别，又是换了一个马甲就不会了系列。还是要用DP来做，我们可以用三维DP数组，也可以用二维DP数组来做，这里为了省空间，我们就用二维DP数组来做，其中dp[i][j]表示在棋盘(i, j)位置上走完当前步骤还留在棋盘上的走法总和，初始化为1，我们其实将步骤这个维度当成了时间维度在不停更新。好，下面我们先写出8种‘日’字走法的位置的坐标，就像之前遍历迷宫上下左右四个方向坐标一样，这不过这次位置变了而已。然后我们一步一步来遍历，每一步都需要完整遍历一遍棋盘的每个位置，新建一个临时数组t，大小和dp数组相同，但是初始化为0，然后对于遍历到的棋盘上的每一个格子，我们都遍历8中解法，如果新的位置不在棋盘上了，直接跳过，否则就加上上一步中的dp数组中对应的值，遍历完棋盘后，将dp数组更新为这个临时数组t.

https://www.geeksforgeeks.org/probability-knight-remain-chessboard/

One thing that we can observe is that at every step the Knight has 8 choices to choose from. Suppose, the Knight has to take k steps and after taking the Kth step the knight reaches (x,y). There are 8 different positions from where the Knight can reach to (x,y) in one step, and they are: (x+1,y+2), (x+2,y+1), (x+2,y-1), (x+1,y-2), (x-1,y-2), (x-2,y-1), (x-2,y+1), (x-1,y+2).
What if we already knew the probabilities of reaching these 8 positions after K-1 steps? Then, the final probability after K steps will simply be equal to the (Σ probability of reaching each of these 8 positions after K-1 steps)/8;
Here we are dividing by 8 because each of these 8 positions have 8 choices and position (x,y) is one of the choice.
For the positions that lie outside the board, we will either take their probabilities as 0 or simply neglect it.

Since, we need to keep track of the probabilities at each position for every number of steps, we need Dynamic Programming to solve this problem.
We are going to take an array dp[x][y][steps] which will store the probability of reaching (x,y) after (steps) number of moves.
Base case : if number of steps is 0, then the probability that the Knight will remain inside the board is 1.

https://leetcode.com/problems/knight-probability-in-chessboard/discuss/113954/Evolve-from-recursive-to-dpbeats-94

https://leetcode.com/problems/knight-probability-in-chessboard/discuss/113955/Solution-with-DP-and-Memoization

recursive version(TLE):

class Solution {
    private int[][]dir = new int[][]{{-2,-1},{-1,-2},{1,-2},{2,-1},{2,1},{1,2},{-1,2},{-2,1}};
    public double knightProbability(int N, int K, int r, int c) {
        return find(N,K,r,c);
    }
    public double find(int N,int K,int r,int c){
        if(r < 0 || r > N - 1 || c < 0 || c > N - 1) return 0;
        if(K == 0)  return 1;
        double rate = 0;
        for(int i = 0;i < dir.length;i++){
            rate += 0.125 * find(N,K - 1,r + dir[i][0],c + dir[i][1]);
        }
        return rate;
    }
}

DFS + cache version:

class Solution {
    private int[][]dir = new int[][]{{-2,-1},{-1,-2},{1,-2},{2,-1},{2,1},{1,2},{-1,2},{-2,1}};
    private double[][][] dp;
    public double knightProbability(int N, int K, int r, int c) {
        dp = new double[N][N][K + 1];
        return find(N,K,r,c);
    }
    public double find(int N,int K,int r,int c){
        if(r < 0 || r > N - 1 || c < 0 || c > N - 1) return 0;
        if(K == 0)  return 1;
        if(dp[r][c][K] != 0) return dp[r][c][K];
        double rate = 0;
        for(int i = 0;i < dir.length;i++)   rate += 0.125 * find(N,K - 1,r + dir[i][0],c + dir[i][1]);
        dp[r][c][K] = rate;
        return rate;
    }
}

https://github.com/cherryljr/LeetCode/blob/master/Knight%20Probability%20in%20Chessboard.java

 * Approach 3: DFS with Memoization
 * 因为 Approach 2 的暴力方法挂了...分析发现各个位置存在大量重复计算。
 * 因此使用一个数组将其计算结果存储起来即可，当有需要时就可以直接调用，即 记忆化搜索。
 * 我们需要记录的状态信息有：行坐标，列坐标，以及步数信息。
 * 因此我们开辟了一个 三维数组 dp[][][].来存储相应的信息。
 * 当前状态依赖于下一步的 8 个状态（走法）。K 指的是 剩余步数
 * 即：dp[row][col][K] += dp[nextRow][nextCol][K - 1];    // 步数-1
 *
 * 时间复杂度：O(N^2*K)
 * 空间复杂度：O(N^2*K)

    class Mesg {
        int row, col;
        int leftStep;

        public Mesg(int row, int col, int leftStep) {
            this.row = row;
            this.col = col;
            this.leftStep = leftStep;
        }
    }

    public double knightProbability(int N, int K, int r, int c) {
        Queue<Mesg> queue = new LinkedList<>();
        queue.offer(new Mesg(r, c, K));
        int[][] dirs = new int[][]{{-1, -2}, {-2,  -1}, {-2, 1}, {-1, 2}, {1, -2}, {2, -1}, {2, 1}, {1, 2}};

        double inBoard = 0;
        while (!queue.isEmpty()) {
            Mesg curr = queue.poll();
            if (curr.leftStep == 0) {
                inBoard += 1;
                continue;
            }

            for (int[] dir : dirs) {
                int nextRow = curr.row + dir[0];
                int nextCol = curr.col + dir[1];
                if (nextRow < 0 || nextRow >= N || nextCol < 0 || nextCol >= N || curr.leftStep <= 0) {
                    continue;
                }
                queue.offer(new Mesg(nextRow, nextCol, curr.leftStep - 1));
            }
        }

        return inBoard / Math.pow(8, K);
    }

https://www.acwing.com/solution/LeetCode/content/699/

X. BFS

 * Approach 1: BFS (Time Limit Exceeded)
 * 相当暴力的做法...利用 BFS 的模板写就行了。
 * 因为我们需要 位置信息 和 剩余次数信息 来进行判断，所以这里建立了一个 Mesg类。
 * 当然这个做法会超时...(这个解法直接跳过也无所谓...只是某人要看就写出来了...)
    class Mesg {
        int row, col;
        int leftStep;

        public Mesg(int row, int col, int leftStep) {
            this.row = row;
            this.col = col;
            this.leftStep = leftStep;
        }
    }

    public double knightProbability(int N, int K, int r, int c) {
        Queue<Mesg> queue = new LinkedList<>();
        queue.offer(new Mesg(r, c, K));
        int[][] dirs = new int[][]{{-1, -2}, {-2,  -1}, {-2, 1}, {-1, 2}, {1, -2}, {2, -1}, {2, 1}, {1, 2}};

        double inBoard = 0;
        while (!queue.isEmpty()) {
            Mesg curr = queue.poll();
            if (curr.leftStep == 0) {
                inBoard += 1;
                continue;
            }

            for (int[] dir : dirs) {
                int nextRow = curr.row + dir[0];
                int nextCol = curr.col + dir[1];
                if (nextRow < 0 || nextRow >= N || nextCol < 0 || nextCol >= N || curr.leftStep <= 0) {
                    continue;
                }
                queue.offer(new Mesg(nextRow, nextCol, curr.leftStep - 1));
            }
        }

        return inBoard / Math.pow(8, K);
    }

X. BFS + Path Compression
https://leetcode.com/problems/knight-probability-in-chessboard/discuss/245509/Easy-python-BFS-beat-85
- same as dp

    def knightProbability(self, N, K, r, c):
        if K == 0:
            return 1.0
        cnt = 0
        cur = {(r,c):1}
        for move in range(K):
            visited = {}
            for coord in cur:
                for i,j in ((-1, -2), (-2, -1), (-2, 1), (-1, 2), (1, 2), (2, 1), (2, -1), (1, -2)):
                    ni,nj = coord[0]+i,coord[1]+j
                    if ni >= 0 and ni < N and nj >= 0 and nj < N:
                        if (ni,nj) in visited:
                            visited[(ni,nj)] += cur[coord]
                        else:
                            visited[(ni,nj)] = cur[coord]
            cur = visited
        return float(sum(visited.values()))/8**K

private static final int[][] direction = new int[][] { { 1, 2 }, { 1, -2 }, { -1, 2 }, { -1, -2 }, { 2, 1 }, { 2, -1 }, { -2, 1 },

    { -2, -1 } };

// k moves, n*n board, starts at r, c

// n, k starts with 1

public double knightProbability(int n, int k, int r, int c) {

  Queue<Element> queue = new ArrayDeque<>();

  queue.add(new Element(r, c, 1));

  while (k > 0) {

    k--;

    int size = queue.size();

    Map<Integer, Double> cache = new HashMap<>();

    for (int i = 0; i < size; i++) {

      Element cur = queue.poll();

      for (int j = 0; j < direction.length; j++) {

        int newRol = cur.row + direction[j][0];

        int newCol = cur.col + direction[j][1];

        if (isValid(newRol, newCol, n)) {

          int key = newRol * n + newCol;

          cache.put(key, cache.getOrDefault(key, 0d) + cur.prob / 8);

        }

        // queue.add(new Element(newRol, newCol, cur.step + 1, cur.prob / 8));

      }

    }

    for (Entry<Integer, Double> entry : cache.entrySet()) {

      queue.add(new Element(entry.getKey() / n, entry.getKey() % n, entry.getValue()));

    }

  }

  double totalPro = 0;

  // for (int i = 0; i < queue.size(); i++) {

  while (!queue.isEmpty()) {

    totalPro += queue.poll().prob;

  }

  return totalPro;

}

private boolean isValid(int row, int col, int n) {

  return row >= 0 && row <= n - 1 && col >= 0 && col <= n - 1;

}

private static class Element {

  public final int row, col;

  public double prob;

  public Element(int row, int col, double prob) {

    super();

    this.row = row;

    this.col = col;

    this.prob = prob;

  }

  @Override

  public String toString() {

    return "Element [row=" + row + ", col=" + col + ", prob=" + prob + "]";

  }

}
https://blog.csdn.net/u014688145/article/details/78153497

一开始采用BFS来遍历所有情况，但在OJ上内存溢出且超时了，主要原因在于BFS把所有的状态都跑一边，而此处K相对较大，N却较小，所以骑士在经过k步之后，很有可能在图中经过相同的点，只是对应的k不同罢了。

这里遇到重复子问题的多次计算，定义问题为f(i, j, k)表示当前坐标(i, j)下，骑士k次移动后的概率。如何划分子问题呢？因为它有八个方向可以移动，所以有：f(i + d[x][0], j + d[x][1], k - 1), x = 1,2,...,8，表示移动到八个位置的其中一个后，原问题变成了如上子问题。

所以，我们有递归+记忆化的手段
// wrong answer
    int[][] dir = {{2, 1},{2, -1},{-2, -1},{-2, 1},{1, 2},{1, -2},{-1, 2},{-1, -2}};

    class Pair{
        int id;
        double pro;

        Pair(int id, double pro){
            this.id = id;
            this.pro = pro;
        }
    }

    public double knightProbability(int N, int K, int r, int c) {

        Queue<Pair> queue = new ArrayDeque<>();
        queue.offer(new Pair(r * N + c, 1));

        int turn = 0;
        while (!queue.isEmpty()) {
            int size = queue.size();
            for (int i = 0; i < size; ++i) {
                Pair p = queue.poll();
                int cnt = 0;
                List<Integer> tmp = new ArrayList<>();
                for (int[] d : dir) {
                    int nx = d[0] + p.id / N;
                    int ny = d[1] + p.id % N;
                    if (check(nx, ny, N)) {
                        cnt ++;
                        tmp.add(nx * N + ny);
                    }
                }
                for (int j = 0; j < tmp.size(); ++j) {
                    queue.offer(new Pair(tmp.get(j), p.pro * cnt / 8));
                }
            }
            turn ++;
            if (turn == K) break;
        }

        double ans = 0;
        int size = queue.size();
        while (!queue.isEmpty()) {
            ans += (queue.poll().pro / size);
        }

        return ans;
    }

    boolean check(int i, int j, int N) {
        return i >= 0 && i < N && j >= 0 && j < N;
    }

X. Approach #2: Matrix Exponentiation

The recurrence expressed in Approach #1 expressed states that transitioned to a linear combination of other states. Any time this happens, we can represent the entire transition as a matrix of those linear combinations. Then, the $n$-th power of this matrix represents the transition of $n$ moves, and thus we can reduce the problem to a problem of matrix exponentiation.

Algorithm

First, there is a lot of symmetry on the board that we can exploit. Naively, there are $N^2$ possible states the knight can be in (assuming it is on the board). Because of symmetry through the horizontal, vertical, and diagonal axes, we can assume that the knight is in the top-left quadrant of the board, and that the column number is equal to or larger than the row number. For any square, the square that is found by reflecting about these axes to satisfy these conditions will be the canonical index of that square.

This will reduce the number of states from $N^2$ to approximately $\frac{N^2}{8}$, which makes the following (cubic) matrix exponentiation on this $O(\frac{N^2}{8}) \times O(\frac{N^2}{8})$ matrix approximately $8^3$ times faster.

Now, if we know that every state becomes some linear combination of states after one move, then let's write a transition matrix $\mathcal{T}$ of them, where the $i$-th row of $\mathcal{T}$ represents the linear combination of states that the $i$-th state goes to. Then, $\mathcal{T}^n$ represents a transition of $n$ moves, for which we want the sum of the $i$-th row, where $i$is the index of the starting square.

• Time Complexity: $O(N^6 \log(K))$ where $N, K$ are defined as in the problem. There are approximately $\frac{N^2}{8}$canonical states, which makes our matrix multiplication $O(N^6)$. To find the $K$-th power of this matrix, we make $O(\log(K))$ matrix multiplications.
• Space Complexity: $O(N^4)$. The matrix has approximately $\frac{N^4}{64}$ elements.

    public double knightProbability(int N, int K, int sr, int sc) {

        int[] dr = new int[]{-1, -1, 1, 1, -2, -2, 2, 2};

        int[] dc = new int[]{2, -2, 2, -2, 1, -1, 1, -1};

        int[] index = new int[N * N];

        int t = 0;

        for (int r = 0; r < N; r++) {

            for (int c = 0; c < N; c++) {

                if (r * N + c == canonical(r, c, N)) {

                    index[r * N + c] = t;

                    t++;

                } else {

                    index[r * N + c] = index[canonical(r, c, N)];

                }

            }

        }

        double[][] T = new double[t][t];

        int curRow = 0;

        for (int r = 0; r < N; r++) {

            for (int c = 0; c < N; c++) {

                if (r * N + c == canonical(r, c, N)) {

                    for (int k = 0; k < 8; k++) {

                        int cr = r + dr[k], cc = c + dc[k];

                        if (0 <= cr && cr < N && 0 <= cc && cc < N) {

                            T[curRow][index[canonical(cr, cc, N)]] += 0.125;

                        }

                    }

                    curRow++;

                }

            }

        }

        double[] row = matrixExpo(T, K)[index[sr*N + sc]];

        double ans = 0.0;

        for (double x: row) ans += x;

        return ans;

    }

    public int canonical(int r, int c, int N) {

        if (2*r > N) r = N-1-r;

        if (2*c > N) c = N-1-c;

        if (r > c) {

            int t = r;

            r = c;

            c = t;

        }

        return r * N + c;

    }

    public double[][] matrixMult(double[][] A, double[][] B) {

        double[][] ans = new double[A.length][A.length];

        for (int i = 0; i < A.length; i++) {

            for (int j = 0; j < B[0].length; j++) {

                for (int k = 0; k < B.length; k++) {

                    ans[i][j] += A[i][k] * B[k][j];

                }

            }

        }

        return ans;

    }

    public double[][] matrixExpo(double[][] A, int pow) {

        double[][] ans = new double[A.length][A.length];

        for (int i = 0; i < A.length; i++) ans[i][i] = 1;

        if (pow == 0) return ans;

        if (pow == 1) return A;

        if (pow % 2 == 1) return matrixMult(matrixExpo(A, pow-1), A);

        double[][] B = matrixExpo(A, pow / 2);

        return matrixMult(B, B);

    }

然后还有时间，说再问⼀一个题，只说思路路即可，问了了⼀一个Horse在棋盘上
的dp，⽤用bottom up dp做，⾯面试官说convinced，问了了复杂度，就没有
写。
求⻢马⾛走⼏几步可以到达特定⽬目的地，棋盘⽆无限⼤大，中间有些位置不不能⾛走。
⽆无限⼤大棋盘 给两个格⼦子 ⼀一些格⼦子上有障碍物不不能⾛走 问两格⼦子的最短路路
（注意⽆无解情况）
脸书伦敦店面
https://www.1point3acres.com/bbs/forum.php?mod=viewthread&tid=446777
来扣留拔霸，稍有不同，求马走几步可以到达特定目的地，棋盘无限大，中间有些位置不能走。
BFS解决，可是习惯性的觉得马除非被挡，否则肯定能走到目的地，忘了考虑棋盘无限大这个情况，在目的地被挡的情况下，会陷入无限循环。经提示后想到这种情况，但已经没时间给方案了。其实方案也很简单，两头一起开始BFS

因为有两种情况是马不能到达目的地，一是马被不能走的位置包围起来，二是目的地被不能走的位置包围起来。从两头同时出发BFS，他们会在中途相遇（有到达路线），或者其中一边穷举所有能走的路线之后发现被挡住了（没有路线