Massive Algorithms: LeetCode 687 - Longest Univalue Path

LeetCode 687 - Longest Univalue Path

https://leetcode.com/problems/longest-univalue-path/description/

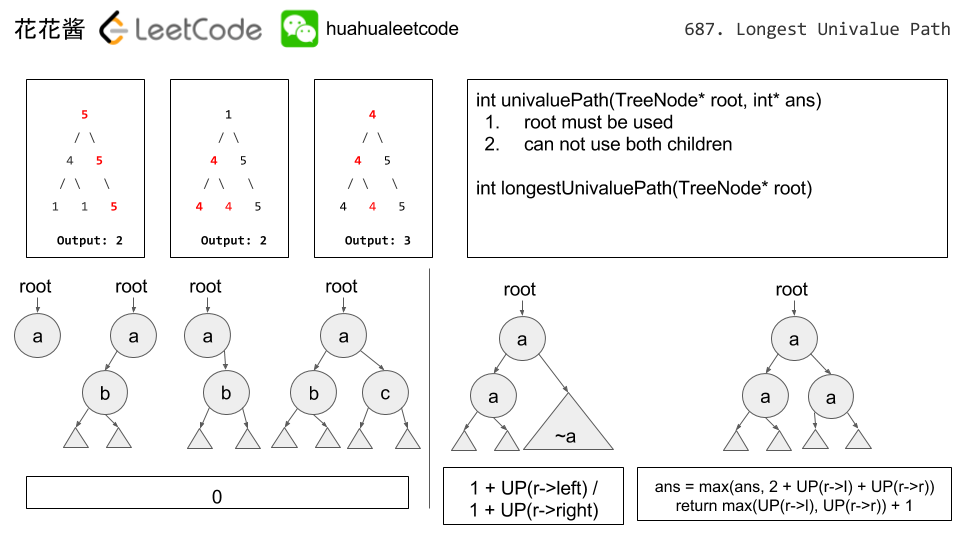
Given a binary tree, find the length of the longest path where each node in the path has the same value. This path may or may not pass through the root.

Note: The length of path between two nodes is represented by the number of edges between them.

Example 1:

Input:

Output:

Example 2:

Input:

Output:

Note: The given binary tree has not more than 10000 nodes. The height of the tree is not more than 1000.

https://medium.com/@rebeccahezhang/leetcode-687-longest-univalue-path-c7791a03c4a0

Intuition: to solve binary tree problem, we can use recursion. We can start analyze three nodes from the leaf node.

                      1 (return:0)
return: max(1,1)=1 //   \\1
       (max:1+1) 4         5
              0// \\0       \\0
               4     4         5
            0// \\0    ...     ...
         null    null

As long as we get the longest path length from the left child and right child, we check if the parent node value = left child value or = right child value. If equal, means the longest path extended by 1.

We then return max (leftMaxLenSoFar, rightMaxLenSoFar) to the parent’s parent node as the longest path so far (only through one side is valid path)

At the same time, we update the global max(the longest path among every candidate path) with max(max, leftMaxLenSoFar + rightMaxLenSoFar).

int max;

public int longestUnivaluePath(TreeNode root) {

max = 0;

longestPath(root);

return max;

}

public int longestPath(TreeNode node) {

// Base case: if null node, return 0

if (node == null) {

return 0;

}

// Get the max length from left and right

int maxLeft = longestPath(node.left);

int maxRight = longestPath(node.right);

// Calculate the current max length

int maxLeftSoFar = 0;

int maxRightSoFar = 0;

// Compare parent node with child node

// If they are the same, extend the max length by one

if (node.left != null && node.left.val == node.val) {

maxLeftSoFar = maxLeft + 1;

}

if (node.right != null && node.right.val == node.val) {

maxRightSoFar = maxRight + 1;

}

// Update the max with the sum of left and right length

max = Math.max(max, maxLeftSoFar + maxRightSoFar);

// Return the max from left and right to upper node

// since only one side path is valid

return Math.max(maxLeftSoFar, maxRightSoFar);

}

https://blog.csdn.net/fuxuemingzhu/article/details/79248926

定义的DFS函数是获得在通过root节点的情况下，最长单臂路径。其中更新的res是左右臂都算上的。所以这个题和普通的题是有点不一样。

要有一种大局观，一个方法给我返回单独子树的最大长度，然后自己比较根节点和左右子树根节点的值就可以了。

http://www.cnblogs.com/grandyang/p/7636259.html

这道题让我们求最长的相同值路径，跟之前那道 Count Univalue Subtrees 十分的类似，解法也很类似。对于这种树的路径问题，递归是不二之选。在递归函数中，我们首先对其左右子结点调用递归函数，得到其左右子树的最大相同值路径长度，下面就要来看当前结点和其左右子结点之间的关系了，如果其左子结点存在且和当前节点值相同，则left自增1，否则left重置0；同理，如果其右子结点存在且和当前节点值相同，则right自增1，否则right重置0。然后用left+right来更新结果res。而调用当前节点值的函数只能返回left和right中的较大值，因为如果还要跟父节点组path，就只能在左右子节点中选一条path，当然选值大的那个了，什么意思呢，举个例子来说吧，比如下面的这棵二叉树：

若此时的node是只有两个结点的第二层的那个结点4，那么分别对其左右子结点调用递归，会得到 left = 1, right = 0，因为此时要跟结点4组成path，所以肯定挑左子结点（有两个4的那条边），那你会问为啥不能连上右子结点的那个4，这整条长度为3的path（left+right，此时的left和right已经分别自增1了，left=2，right=1）其实我们已经用来更新过结果res了。需要注意的是我们的递归函数helper返回值的意义，并不是经过某个结点的最长路径的长度，最长路径长度保存在了结果res中，不是返回值，返回的是以该结点为终点的最长路径长度，这样回溯的时候，我们还可以继续连上其父结点，比如若根结点也是4的话，那么回溯到根结点的时候，路径长度又可以增加了

https://leetcode.com/problems/longest-univalue-path/discuss/108136/JavaC%2B%2B-Clean-Code

Longest-Univalue-Path of a tree is among those Longest-Univalue-Path-Across at each node;
Longest-Univalue-Path-Across a node is sum of { Longest-Univalue-Path-Start-At each child with same value } + 1
Let an dfs to return Longest-Univalue-Path-Start-At each node, the Longest-Univalue-Path-Across node can be calculated by combine the Longest-Univalue-Path-Start-At of its 2 child; and we can use an global variable res to hold the max value and compare with each intermediate result.

l is the length of single direction Longest-Univalue-Path start from left-child,
r is the length of single direction Longest-Univalue-Path start from right-child,
resl is the length of single direction Longest-Univalue-Path start from parent go left,
resr is the length of single direction Longest-Univalue-Path start from parent go right.
int dfs(node) returns the Longest-Univalue-Path-Start-At that node, and update the result of Longest-Univalue-Path-Across that node through side effect.
It is really hard to name those variables to reflect these concept.

Example:

                ...
               /   
              4 (res = resl + resr = 3)
  (resl = 2) / \ (resr= 1)
    (l = 1) 4   4 (r = 0)
           /     
          4

resl is Longest-Univalue-Path-Start-At left node + 1,
resr is Longest-Univalue-Path-Start-At right node + 1,
in here the local result of Longest-Univalue-Path-Across at this node is the sum of the 2

    public int longestUnivaluePath(TreeNode root) {
        int[] res = new int[1];
        if (root != null) dfs(root, res);
        return res[0];
    }

    private int dfs(TreeNode node, int[] res) {
        int l = node.left != null ? dfs(node.left, res) : 0; // Longest-Univalue-Path-Start-At - left child
        int r = node.right != null ? dfs(node.right, res) : 0; // Longest-Univalue-Path-Start-At - right child
        int resl = node.left != null && node.left.val == node.val ? l + 1 : 0; // Longest-Univalue-Path-Start-At - node, and go left
        int resr = node.right != null && node.right.val == node.val ? r + 1 : 0; // Longest-Univalue-Path-Start-At - node, and go right
        res[0] = Math.max(res[0], resl + resr); // Longest-Univalue-Path-Across - node
        return Math.max(resl, resr);
    }

We can think of any path (of nodes with the same values) as up to two arrows extending from it's root.

Specifically, the root of a path will be the unique node such that the parent of that node does not appear in the path, and an arrow will be a path where the root only has one child node in the path.

Then, for each node, we want to know what is the longest possible arrow extending left, and the longest possible arrow extending right? We can solve this using recursion.

Algorithm

Let arrow_length(node) be the length of the longest arrow that extends from the node. That will be 1 + arrow_length(node.left) if node.left exists and has the same value as node. Similarly for the node.right case.

While we are computing arrow lengths, each candidate answer will be the sum of the arrows in both directions from that node. We record these candidate answers and return the best one.

int ans;
public int longestUnivaluePath(TreeNode root) {
ans = 0;
arrowLength(root);
return ans;
}
public int arrowLength(TreeNode node) {
if (node == null) return 0;
int left = arrowLength(node.left)
int right = arrowLength(node.right);
int arrowLeft = 0, arrowRight = 0;
if (node.left != null && node.left.val == node.val) {
arrowLeft += left + 1;
}
if (node.right != null && node.right.val == node.val) {
arrowRight += right + 1;
}
ans = Math.max(ans, arrowLeft + arrowRight);
return Math.max(arrowLeft, arrowRight);
}

https://leetcode.com/problems/longest-univalue-path/discuss/108136/JavaC++-Clean-Code

Longest-Univalue-Path of a tree is among those Longest-Univalue-Path-Across at each node;
Longest-Univalue-Path-Across a node is sum of { Longest-Univalue-Path-Start-At each child with same value } + 1
Let an dfs to return Longest-Univalue-Path-Start-At each node, the Longest-Univalue-Path-Across node can be calculated by combine the Longest-Univalue-Path-Start-At of its 2 child; and we can use an global variable res to hold the max value and compare with each intermediate result.

Example:

                ...
               /   
              4 (res = resl + resr = 3)
  (resl = 2) / \ (resr= 1)
    (l = 1) 4   4 (r = 0)
           /     
          4

    public int longestUnivaluePath(TreeNode root) {
        int[] res = new int[1];
        if (root != null) dfs(root, res);
        return res[0];
    }

    private int dfs(TreeNode node, int[] res) {
        int l = node.left != null ? dfs(node.left, res) : 0; // Longest-Univalue-Path-Start-At - left child
        int r = node.right != null ? dfs(node.right, res) : 0; // Longest-Univalue-Path-Start-At - right child
        int resl = node.left != null && node.left.val == node.val ? l + 1 : 0; // Longest-Univalue-Path-Start-At - node, and go left
        int resr = node.right != null && node.right.val == node.val ? r + 1 : 0; // Longest-Univalue-Path-Start-At - node, and go right
        res[0] = Math.max(res[0], resl + resr); // Longest-Univalue-Path-Across - node
        return Math.max(resl, resr);
    }

    int longestUnivaluePath(TreeNode* root) {
        int res = 0;
        if (root) helper(root, root->val, res);
        return res;
    }
    int helper(TreeNode* node, int parent, int& res) {
        if (!node) return 0;
        int left = helper(node->left, node->val, res);
        int right = helper(node->right, node->val, res);
        res = max(res, left + right);
        if (node->val == parent) return max(left, right) + 1;
        return 0;
    }

https://leetcode.com/problems/longest-univalue-path/discuss/130315/Java-Solution-With-Explanation

What we need is a longest path with same number and this path could pass through any node. So we must visit each node and workout a logic to know the longest path at that node, while we are at the given node, we keep updating max known path so far.

Visiting each node
this is just tree traversal

Logic for longest path at the given node
Two parts here
One is to update maxLength at this node. There are three possibilites:

longest path is in the left subtree but doesn't connect to me
longest path is in the right subtree but doesn't connect to me
longest path goes through me

All of these are captured by l+r in the code.

Second pat is what we need to return to our caller/parent node
Since this is a simple path problem, for the caller we must tell which path we are choosing from 1 & 2 above. Why? Because path cannot be in Y shape. So we choose the max in left and right paths. But remember the whole path has to carry the same value - so now make use of the parent value to compare our value, if yes add 1 to the max chosen in the previous statement or return 0 (why? As this node cut the streak of longest path with same value)

int len = 0;
    public int longestUnivaluePath(TreeNode root) {
        if(root != null)         
            longestUnivaluePath(root, -1);
        return len;
    }
    private int longestUnivaluePath(TreeNode curr, int val){
        if(curr == null) return 0;
        int l = longestUnivaluePath(curr.left, curr.val), r = longestUnivaluePath(curr.right, curr.val), count = 0;
        len = Math.max(len, l+r); //l is "valid" connecting edges to me from left
        if(curr.val == val)
            count = 1+Math.max(l,r); //give it to caller max path with same number, include me
        return count;
    }

X. TODO
下面这种解法使用了两个递归函数，使得写法更加简洁了，首先还是先判断root是否为空，是的话返回0。然后对左右子节点分别调用当前函数，取其中较大值保存到变量sub中，表示左右子树中最长的相同值路径，然后就是要跟当前树的最长相同值路径比较，计算方法是对左右子结点调用一个helper函数，并把当前结点值传进去，把返回值加起来和sub比较，取较大值返回。顺便提一下，这里的helper函数的返回值的意义跟解法二中的是一样的。在helper函数里，若当前结点为空，或者当前节点值不等于父结点值的话，返回0。否则结返回对左右子结点分别调用helper递归函数中的较大值加1，我们发现这种写法跟求树的最大深度很像

    int longestUnivaluePath(TreeNode* root) {
        if (!root) return 0;
        int sub = max(longestUnivaluePath(root->left), longestUnivaluePath(root->right));
        return max(sub, helper(root->left, root->val) + helper(root->right, root->val));
    }
    int helper(TreeNode* node, int parent) {
        if (!node || node->val != parent) return 0;
        return 1 + max(helper(node->left, node->val), helper(node->right, node->val));
    }

LeetCode 687 - Longest Univalue Path

Labels

Popular Posts