LeetCode 121 - Best Time to Buy and Sell Stock

LeetCode 121 - Best Time to Buy and Sell Stock
LeetCode - Best Time to Buy and Sell Stock II
LeetCode - Best Time to Buy and Sell Stock III
LeetCode 188 - Best Time to Buy and Sell Stock IV
Leetcode 309 - Best Time to Buy and Sell Stock with Cooldown
https://leetcode.com/problems/best-time-to-buy-and-sell-stock/

Say you have an array for which the ith element is the price of a given stock on day i.

If you were only permitted to complete at most one transaction (ie, buy one and sell one share of the stock), design an algorithm to find the maximum profit.

Example 1:

Input: [7, 1, 5, 3, 6, 4]
Output: 5

max. difference = 6-1 = 5 (not 7-1 = 6, as selling price needs to be larger than buying price)

Example 2:

Input: [7, 6, 4, 3, 1]
Output: 0

In this case, no transaction is done, i.e. max profit = 0.

X. https://leetcode.com/problems/best-time-to-buy-and-sell-stock/discuss/39062/my-jave-accepted-solution-with-on-time-and-o1-space
https://leetcode.com/articles/best-time-to-buy-and-sell-stock/

Say the given array is:

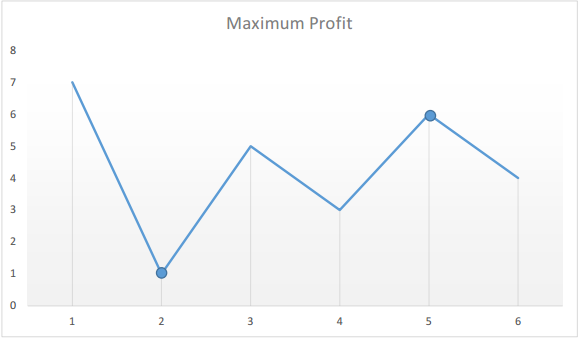
[7, 1, 5, 3, 6, 4]

If we plot the numbers of the given array on a graph, we get:

The points of interest are the peaks and valleys in the given graph. We need to find the largest peak following the smallest valley. We can maintain two variables - minprice and maxprofit corresponding to the smallest valley and maximum profit (maximum difference between selling price and minprice) obtained so far respectively.

    public int maxProfit(int prices[]) {
        int minprice = Integer.MAX_VALUE;
        int maxprofit = 0;
        for (int i = 0; i < prices.length; i++) {
            if (prices[i] < minprice)
                minprice = prices[i];
            else if (prices[i] - minprice > maxprofit)
                maxprofit = prices[i] - minprice;
        }
        return maxprofit;
    }

X. Using Kadane’s Algorithm
https://leetcode.com/problems/best-time-to-buy-and-sell-stock/discuss/39038/Kadane's-Algorithm-Since-no-one-has-mentioned-about-this-so-far-%3A)-(In-case-if-interviewer-twists-the-input)

The logic to solve this problem is same as "max subarray problem" using Kadane's Algorithm. Since no body has mentioned this so far, I thought it's a good thing for everybody to know.

All the straight forward solution should work, but if the interviewer twists the question slightly by giving the difference array of prices, Ex: for {1, 7, 4, 11}, if he gives {0, 6, -3, 7}, you might end up being confused.

Here, the logic is to calculate the difference (maxCur += prices[i] - prices[i-1]) of the original array, and find a contiguous subarray giving maximum profit. If the difference falls below 0, reset it to zero.

    public int maxProfit(int[] prices) {
        int maxCur = 0, maxSoFar = 0;
        for(int i = 1; i < prices.length; i++) {
            maxCur = Math.max(0, maxCur += prices[i] - prices[i-1]);
            maxSoFar = Math.max(maxCur, maxSoFar);
        }
        return maxSoFar;
    }

*maxCur = current maximum value

*maxSoFar = maximum value found so far

• Time complexity : $O(n^2)$. Loop runs $\frac{n (n-1)}{2}$ times.
• Space complexity : $O(1)$. Only two variables - maxprofit and profit are used.

    public int maxProfit(int prices[]) {
        int maxprofit = 0;
        for (int i = 0; i < prices.length - 1; i++) {
            for (int j = i + 1; j < prices.length; j++) {
                int profit = prices[j] - prices[i];
                if (profit > maxprofit)
                    maxprofit = profit;
            }
        }
        return maxprofit;
    }

http://leetcode.com/2010/11/best-time-to-buy-and-sell-stock.html
If you were only permitted to buy one share of the stock and sell one share of the stock, design an algorithm to find the best times to buy and sell.
Find i and j that maximizes Aj – Ai, where i < j.
To solve this problem efficiently, you would need to track the minimum value’s index. As you traverse, update the minimum value’s index when a new minimum is met. Then, compare the difference of the current element with the minimum value. Save the buy and sell time when the difference exceeds our maximum difference (also update the maximum difference).

void getBestTime(int stocks[], int sz, int &buy, int &sell) {

  int min = 0;

  int maxDiff = 0;

  buy = sell = 0;

  for (int i = 0; i < sz; i++) {

    if (stocks[i] < stocks[min])

      min = i;

    int diff = stocks[i] - stocks[min];

    if (diff > maxDiff) {

      buy = min;

      sell = i;

      maxDiff = diff;

    }

  }

}

http://blog.csdn.net/u013027996/article/details/19414967
You may complete as many transactions as you like (ie, buy one and sell one share of the stock multiple times).
However, you may not engage in multiple transactions at the same time (ie, you must sell the stock before you buy again).
http://www.geeksforgeeks.org/stock-buy-sell/
1. Find the local minima and store it as starting index. If not exists, return.
2. Find the local maxima. and store it as ending index. If we reach the end, set the end as ending index.
3. Update the solution (Increment count of buy sell pairs)
4. Repeat the above steps if end is not reached.

1.     public int maxProfit(int[] prices) {  
2.         if(prices == null || prices.length == 0){  
3.             return 0;  
4.         }  
5.         int len = prices.length;  
6.         int maxProfit = 0;  
7.         for(int i = 1; i < len; i++){  
8.             int tempProfit = prices[i] - prices[i-1];  
9.             if(tempProfit > 0){  
10.                 maxProfit += tempProfit;  
11.             }  
12.         }  
13.         return maxProfit;  
14.     } 

void stockBuySell(int price[], int n)

{

    // Prices must be given for at least two days

    if (n == 1)

        return;

    int count = 0; // count of solution pairs

    // solution vector

    Interval sol[n/2 + 1];

    // Traverse through given price array

    int i = 0;

    while (i < n-1)

    {

        // Find Local Minima. Note that the limit is (n-2) as we are

        // comparing present element to the next element.

        while ((i < n-1) && (price[i+1] <= price[i]))

            i++;

        // If we reached the end, break as no further solution possible

        if (i == n-1)

            break;

        // Store the index of minima

        sol[count].buy = i++;

        // Find Local Maxima.  Note that the limit is (n-1) as we are

        // comparing to previous element

        while ((i < n) && (price[i] >= price[i-1]))

            i++;

        // Store the index of maxima

        sol[count].sell = i-1;

        // Increment count of buy/sell pairs

        count++;

    }

    return;

}

http://n00tc0d3r.blogspot.com/2013/01/best-time-to-buy-and-sell-stock.html

In this case, we are allowed to make multiple transactions. So, we can buy the stock at "local valley" (ie minimal) and sell it at "local peak" (ie. maximal) so as to maximize our profit.

 public int maxProfit(int[] prices) {  

   int totalProfit = 0, curProfit = 0, buyDay = 0, sellDay = 1;  

   while (sellDay < prices.length) {  

     if (prices[sellDay] <= prices[sellDay-1]) {  

       totalProfit += curProfit;  

       curProfit = 0;  

       buyDay = sellDay;  

       sellDay++;  

     } else 

       curProfit = Math.max(curProfit, (prices[sellDay++] - prices[buyDay]));  

   } // end-while  

   totalProfit += curProfit;  

   return totalProfit;  

 } 

Best Time to Buy and Sell Stock III
You may complete at most two transactions.
we can use two arrays f[i] and b[i] to record the maximum profit for price[0...i−1] and price[i...n−1] , respectively. After that, we just need to find the maximum of f[i]+b[i].
)
Maximum profit by buying and selling a share at most twice
O(n):

1) Create a table profit[0..n-1] and initialize all values in it 0.

2) Traverse price[] from right to left and update profit[i] such that profit[i] stores maximum profit achievable from one transaction in subarray price[i..n-1]

3) Traverse price[] from left to right and update profit[i] such that profit[i] stores maximum profit such that profit[i] contains maximum achievable profit from two transactions in subarray price[0..i].

4) Return profit[n-1]

int maxProfit(int price[], int n)

{

    // Create profit array and initialize it as 0

    int *profit = new int[n];

    for (int i=0; i<n; i++)

        profit[i] = 0;

    /* Get the maximum profit with only one transaction

       allowed. After this loop, profit[i] contains maximum

       profit from price[i..n-1] using at most one trans. */

    int max_price = price[n-1];

    for (int i=n-2;i>=0;i--)

    {

        // max_price has maximum of price[i..n-1]

        if (price[i] > max_price)

            max_price = price[i];

        // we can get profit[i] by taking maximum of:

        // a) previous maximum, i.e., profit[i+1]

        // b) profit by buying at price[i] and selling at

        //    max_price

        profit[i] = max(profit[i+1], max_price-price[i]);

    }

    /* Get the maximum profit with two transactions allowed

       After this loop, profit[n-1] contains the result */

    int min_price = price[0];

    for (int i=1; i<n; i++)

    {

        // min_price is minimum price in price[0..i]

        if (price[i] < min_price)

            min_price = price[i];

        // Maximum profit is maximum of:

        // a) previous maximum, i.e., profit[i-1]

        // b) (Buy, Sell) at (min_price, price[i]) and add

        //    profit of other trans. stored in profit[i]

        profit[i] = max(profit[i-1], profit[i] +

                                    (price[i]-min_price) );

    }

    int result = profit[n-1];

    delete [] profit; // To avoid memory leak

    return result;

}

Max profit with at most two transactions =
       MAX {max profit with one transaction and subarray price[0..i] +
            max profit with one transaction and aubarray price[i+1..n-1]  }
i varies from 0 to n-1. 

利用动态规划，声明两个数组arrayA，arrayB，其中arrayA[i]表示从0到i买卖一次的最大利润，arrayA[i]可根据arrayA[i-1]计算得到。
        arrayB[i]表示从i到len-1买卖一次的最大利润，逆向思维来求解arrayB[i]，arrayB[i]可根据arrayB[i+1]计算得到。
        这样针对每个i，累加就可以得到最大利润。
http://blog.csdn.net/fightforyourdream/article/details/14503469

1.     // 基本思想是分成两个时间段，然后对于某一天，计算之前的最大值和之后的最大值  
2.     public static int maxProfit(int[] prices) {  
3.         if(prices.length == 0){  
4.             return 0;  
5.         }  
6.         int max = 0;  
7.         // dp数组保存左边和右边的利润最大值  
8.         int[] left = new int[prices.length];        // 计算[0,i]区间的最大值  
9.         int[] right = new int[prices.length];   // 计算[i,len-1]区间的最大值  
10.         process(prices, left, right);  
11.         // O(n)找到最大值  
12.         for(int i=0; i<prices.length; i++){  
13.             max = Math.max(max, left[i]+right[i]);  
14.         }  
15.         return max;  
16.     }  
17.     public static void process(int[] prices, int[] left, int[] right){  
18.         left[0] = 0;  
19.         int min = prices[0];        // 最低买入价  
20.         // 左边递推公式  
21.         for(int i=1; i<left.length; i++){  
22.             left[i] = Math.max(left[i-1], prices[i]-min);   // i的最大利润为（i-1的利润）和（当前卖出价和之前买入价之差）的较大那个  
23.             min = Math.min(min, prices[i]);     // 更新最小买入价  
24.         }  
25.         right[right.length-1] = 0;  
26.         int max = prices[right.length-1];       // 最高卖出价  
27.         // 右边递推公式  
28.         for(int i=right.length-2; i>=0; i--){  
29.             right[i] = Math.max(right[i+1], max-prices[i]); // i的最大利润为（i+1的利润）和（最高卖出价和当前买入价之差）的较大那个  
30.             max = Math.max(max, prices[i]);     // 更新最高卖出价  
31.         }  
32.     }

public class BestTimeToBuyAndSellStockIII {

    public int maxProfit(int[] prices) {

        if (prices == null || prices.length == 0)

            return 0;

        // forward[i]: maximum profit for prices[0...i-1]; forward[0]=0

        int[] forward = new int[prices.length+1];

        int lowestBuyInPrice = prices[0];   // Lowest buy-in price up to now

        for (int i = 2; i <= prices.length; i++) {      // Traverse forwards

            forward[i] = Math.max(forward[i-1], prices[i-1]-lowestBuyInPrice);

            lowestBuyInPrice = Math.min(lowestBuyInPrice, prices[i-1]);

        }

        // backward[i]: maximum profit for prices[i...n-1]

        int[] backward = new int[prices.length];

        int highestSellOutPrice = prices[prices.length-1];   // Lowest buy-in price up to now

        for (int i = prices.length-2; i >= 0; i--) {    // Traverse backwards

            backward[i] = Math.max(backward[i+1], highestSellOutPrice-prices[i]);

            highestSellOutPrice = Math.max(highestSellOutPrice, prices[i]);

        }

        // Find the maximum of forward[i]+backward[i]

        int maximumProfit = 0;

        for (int i = 0; i < prices.length; i++) {

            maximumProfit = Math.max(maximumProfit, forward[i]+backward[i]);

        }

        return maximumProfit;

    }

}

You can complete K transaction
我们还是使用“局部最优和全局最优解法”。我们维护两种量，一个是当前到达第i天可以最多进行j次交易，最好的利润是多少（global[i][j]），另一个是当前到达第i天，最多可进行j次交易，并且最后一次交易在当天卖出的最好的利润是多少（local[i][j]）。下面我们来看递推式，全局的比较简单，
global[i][j]=max(local[i][j],global[i-1][j])，

也就是去当前局部最好的，和过往全局最好的中大的那个（因为最后一次交易如果包含当前天一定在局部最好的里面，否则一定在过往全局最优的里面）。对于局部变量的维护，递推式是
local[i][j]=max(global[i-1][j-1]+max(diff,0),local[i-1][j]+diff)，

也就是看两个量，第一个是全局到i-1天进行j-1次交易，然后加上今天的交易，如果今天是赚钱的话（也就是前面只要j-1次交易，最后一次交易取当前天），第二个量则是取local第i-1天j次交易，然后加上今天的差值（这里因为local[i-1][j]比如包含第i-1天卖出的交易，所以现在变成第i天卖出，并不会增加交易次数，而且这里无论diff是不是大于0都一定要加上，因为否则就不满足local[i][j]必须在最后一天卖出的条件了）。

上面的算法中对于天数需要一次扫描，而每次要对交易次数进行递推式求解，所以时间复杂度是O(n*k)，如果是最多进行两次交易，那么复杂度还是O(n)。空间上只需要维护当天数据皆可以，所以是O(k)，当k=2，则是O(1)
这里的模型是比较复杂的，主要是在递推式中，local和global是交替求解的。

1.     public int max(int[] prices, int k) {       // k: k times transactions  
2.         int len = prices.length;  
3.         if(len == 0) {  
4.             return 0;  
5.         }  
6.         int[][] local = new int[len][k+1];      // local[i][j]: max profit till i day, j transactions, where there is transaction happening on i day  
7.         int[][] global = new int[len][k+1];     // global[i][j]: max profit across i days, j transactions  
8.         for(int i=1; i<len; i++) {  
9.             int diff = prices[i] - prices[i-1];  
10.             for(int j=1; j<=k; j++) {  
11.                 local[i][j] = Math.max(global[i-1][j-1]+Math.max(diff,0), local[i-1][j]+diff);  
12.                 global[i][j] = Math.max(global[i-1][j], local[i][j]);  
13.             }  
14.         }  
15.         return global[len-1][k];  
16.     }  

Solution from EPI
  static int maxKPairsProfits(List<Integer> A, int k) {
    List<Integer> kSum = new ArrayList<Integer>(k << 1);
    fill(kSum, k << 1, Integer.MIN_VALUE);

    for (int i = 0; i < A.size(); ++i) {
      List<Integer> preKSum = new ArrayList<Integer>(kSum);

      for (int j = 0, sign = -1; j < kSum.size() && j <= i; ++j, sign *= -1) {
        int diff = sign * A.get(i) + (j == 0 ? 0 : preKSum.get(j - 1));
        kSum.set(j, max(diff, preKSum.get(j)));
      }
    }

    return kSum.get(kSum.size() - 1); // returns the last selling profits as the answer.
  }

http://www.1point3acres.com/bbs/thread-160113-1-1.html

• Buy and sell stock1变种。面试官在编故事，说要给fitbit加一个feature，能记录体重并且在用户减肥达到一定数量时给出congratulations之类的奖励……输入一个数组，存的是fitbit用户每日体重…求一段时间内用户体重最多下降了多少(maximum weight loss)。

Read full article from Sell Stock | Darren's Blog