Massive Algorithms: LeetCode 543 - Diameter of a Binary Tree

LeetCode 543 - Diameter of a Binary Tree

Diameter of a Binary Tree | GeeksforGeeks
The diameter of a tree (sometimes called the width) is the number of nodes on the longest path between two leaves in the tree

The diameter of a tree T is the largest of the following quantities:

* the diameter of T’s left subtree
* the diameter of T’s right subtree
* the longest path between leaves that goes through the root of T (this can be computed from the heights of the subtrees of T)

Optimized implementation: The above implementation can be optimized by calculating the height in the same recursion rather than calling a height() separately. This optimization reduces time complexity to O(n).

https://leetcode.com/articles/diameter-of-binary-tree/

Any path can be written as two arrows (in different directions) from some node, where an arrow is a path that starts at some node and only travels down to child nodes.

If we knew the maximum length arrows L, R for each child, then the best path touches L + R + 1nodes.

Algorithm

Let's calculate the depth of a node in the usual way: max(depth of node.left, depth of node.right) + 1. While we do, a path "through" this node uses 1 + (depth of node.left) + (depth of node.right) nodes. Let's search each node and remember the highest number of nodes used in some path. The desired length is 1 minus this number.

https://codeforces.com/blog/entry/20935

Given a tree T of N nodes, calculate longest path between any two nodes(also known as diameter of tree).

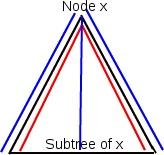
First, lets root tree at node 1. Now, we need to observe that there would exist a node x such that:

Longest path starts from node x and goes into its subtree(denoted by blue lines in the image). Lets define by f(x) this path length.
Longest path starts in subtree of x, passes through x and ends in subtree of x(denoted by red line in image). Lets define by g(x) this path length.

If for all nodes x, we take maximum of f(x), g(x), then we can get the diameter. But first, we need to see how we can calculate maximum path length in both cases.

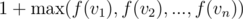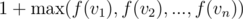Now, lets say a node V has n children v1, v2, ..., vn. We have defined f(i) as length of longest path that starts at node i and ends in subtree of i. We can recursively define f(V) as $\text{[math]}$ , because we are looking at maximum path length possible from children of V and we take the maximum one. So, optimal substructure is being followed here. Now, note that this is quite similar to DP except that now we are defining functions for nodes and defining recursion based on values of children. This is what DP on trees is.

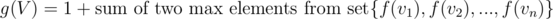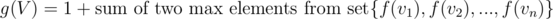Now, for case 2, a path can originate from subtree of node vi, and pass through node V and end in subtree of vj, where i ≠ j. Since, we want this path length to be maximum, we'll choose two children vi and vj such that f(vi) and f(vj) are maximum. We say that $\text{[math]}$ .

For implementing this, we note that for calculating f(V), we need f to be calculated for all children of V. So, we do a DFS and we calculate these values on the go. See this implementation for details.

If you can get the two maximum elements in O(n), where n is number of children then total complexity will be O(N), since we do this for all the nodes in tree.

//adjacency list
//adj[i] contains all neighbors of i
vector<int> adj[N];

//functions as defined above
int f[N],g[N],diameter;

//pV is parent of node V
void dfs(int V, int pV){
    //this vector will store f for all children of V
    vector<int> fValues;

    //traverse over all children
    for(auto v: adj[V]){
    if(v == pV) continue;
    dfs(v, V);
    fValues.push_back(f[v]);
    }

    //sort to get top two values
    //you can also get top two values without sorting(think about it) in O(n)
    //current complexity is n log n
    sort(fValues.begin(),fValues.end());

    //update f for current node
    f[V] = 1;
    if(not fValues.empty()) f[V] += fValues.back();

    if(fValues.size()>=2)
         g[V] = 2 + fValues.back() + fValues[fValues.size()-2];

    diameter = max(diameter, max(f[V], g[V]));
}

http://algorithms.tutorialhorizon.com/diameter-of-a-binary-tree/

Every node will return the two information in the same iteration , height of that node and diameter of tree with respect to that node.

public int[] Diameter(Node root) {
int DandH[] = { 0, 0 }; // initialize the height (DandH[0]) and diameter
// as 0 (DandH[1])
if (root != null) {

int[] leftResult = Diameter(root.left);
int[] rightResult = Diameter(root.right);

int height = Math.max(leftResult[0], rightResult[0]) + 1;
int leftDiameter = leftResult[1];
int rightDiameter = rightResult[1];
int rootDiameter = leftResult[0] + rightResult[0] + 1;
int finalDiameter = getMax(leftDiameter, rightDiameter,
rootDiameter);
// prepare the DandH[]
DandH[0] = height; // update the height
DandH[1] = finalDiameter;
return DandH;
}
return DandH;
}
https://discuss.leetcode.com/topic/83456/java-solution-maxdepth

For every node, length of longest path which pass it = MaxDepth of its left subtree + MaxDepth of its right subtree.

    int max = 0;
    
    public int diameterOfBinaryTree(TreeNode root) {
        maxDepth(root);
        return max;
    }
    
    private int maxDepth(TreeNode root) {
        if (root == null) return 0;
        
        int left = maxDepth(root.left);
        int right = maxDepth(root.right);
        
        max = Math.max(max, left + right);
        
        return Math.max(left, right) + 1;
    }

same here without the member variable using 2 value return instead.

    public int DiameterOfBinaryTree(TreeNode root) {
        return DFS(root)[0];
    }
    
    // int[2] = [best, height]
    private int[] DFS(TreeNode node)
    {
        if (node == null) return new int[] { 0, 0 };
        int[] left = DFS(node.left);
        int[] right = DFS(node.right);
        
        int best = Math.Max(left[1] + right[1], Math.Max(left[0], right[0]));
        int height = 1 + Math.Max(left[1], right[1]);
        return new int[] { best, height };
    }

https://discuss.leetcode.com/topic/83471/c-java-clean-code

    public int diameterOfBinaryTree(TreeNode root) {
        int[] diameter = new int[1];
        height(root, diameter);
        return diameter[0];        
    }

    private int height(TreeNode node, int[] diameter) {
        if (node == null) {
            return 0;
        }
        int lh = height(node.left, diameter);
        int rh = height(node.right, diameter);
        diameter[0] = Math.max(diameter[0], lh + rh);
        return 1 + Math.max(lh, rh);
    }

Time Complexity: O(n)

// A utility class to pass heigh object

class Height

{

    int h;

}

    /* define height =0 globally and  call diameterOpt(root,height)

       from main */

    int diameterOpt(Node root, Height height)

    {

        /* lh --> Height of left subtree

           rh --> Height of right subtree */

        Height lh = new Height(), rh = new Height();

        if (root == null)

        {

            height.h = 0;

            return 0; /* diameter is also 0 */

        }

        /* ldiameter  --> diameter of left subtree

           rdiameter  --> Diameter of right subtree */ 

        /* Get the heights of left and right subtrees in lh and rh

         And store the returned values in ldiameter and ldiameter */

        lh.h++;     rh.h++; 

        int ldiameter = diameterOpt(root.left, lh);

        int rdiameter = diameterOpt(root.right, rh);

        /* Height of current node is max of heights of left and

         right subtrees plus 1*/

        height.h = Math.max(lh.h, rh.h) + 1;

        return Math.max(lh.h + rh.h + 1, Math.max(ldiameter, rdiameter));

    }

    /* A wrapper over diameter(Node root) */

    int diameter()

    {

        Height height = new Height();

        return diameterOpt(root, height);

    }

Alternative SolutionTime Complexity: O(n^2)

    int diameter(Node root)

    {

        /* base case if tree is empty */

        if (root == null)

            return 0;

        /* get the height of left and right sub trees */

        int lheight = height(root.left);

        int rheight = height(root.right);

        /* get the diameter of left and right subtrees */

        int ldiameter = diameter(root.left);

        int rdiameter = diameter(root.right);

        /* Return max of following three

          1) Diameter of left subtree

         2) Diameter of right subtree

         3) Height of left subtree + height of right subtree + 1 */

        return Math.max(lheight + rheight + 1,

                        Math.max(ldiameter, rdiameter));

    }

    /* A wrapper over diameter(Node root) */

    int diameter()

    {

        return diameter(root);

    }

    /*The function Compute the "height" of a tree. Height is the

      number f nodes along the longest path from the root node

      down to the farthest leaf node.*/

    static int height(Node node)

    {

        /* base case tree is empty */

        if (node == null)

            return 0;

        /* If tree is not empty then height = 1 + max of left

           height and right heights */

        return (1 + Math.max(height(node.left), height(node.right)));

    }

http://bylijinnan.iteye.com/blog/1341532

private int maxLen=0;

public void findMaxLen(Node node){
if(node==null) return ;
if(node.getLeft()==null){
node.setMaxLeftLen(0);
}
if(node.getRight()==null){
node.setMaxRightLen(0);
}
if(node.getLeft()!=null){
findMaxLen(node.getLeft());
}
if(node.getRight()!=null){
findMaxLen(node.getRight());
}
if(node.getLeft()!=null){
int temp=0;
Node left=node.getLeft();
if(left.getMaxLeftLen()>left.getMaxRightLen()){
temp=left.getMaxLeftLen();
}else{
temp=left.getMaxRightLen();
}
node.setMaxLeftLen(temp+1);
}
if(node.getRight()!=null){
int temp=0;
Node right=node.getRight();
if(right.getMaxLeftLen()>right.getMaxRightLen()){
temp=right.getMaxLeftLen();
}else{
temp=right.getMaxRightLen();
}
node.setMaxRightLen(temp+1);
}
if(maxLen<node.getMaxLeftLen()+node.getMaxRightLen()){
maxLen=node.getMaxLeftLen()+node.getMaxRightLen();
}
}

Also check http://justprogrammng.blogspot.in/2012/06/longest-path-between-any-two-nodes-of.html#.U8WeSfldVyw

Compute the diameter of a generic tree - not a binary tree

TreeDiameter.java
public static class TreeNode {
List<Pair<TreeNode, Double>> edges = new ArrayList<>();
}
public static double computeDiameter(TreeNode T) {
return T != null ? computeHeightAndDiameter(T).getSecond() : 0.0;
}

// Returns (height, diameter) pair.
private static Pair<Double, Double> computeHeightAndDiameter(TreeNode r) {
double diameter = Double.MIN_VALUE;
double[] height = {0.0, 0.0}; // Stores the max two heights.
for (Pair<TreeNode, Double> e : r.edges) {
Pair<Double, Double> heightDiameter = computeHeightAndDiameter(e
.getFirst());
if (heightDiameter.getFirst() + e.getSecond() > height[0]) {
height[1] = height[0];
height[0] = heightDiameter.getFirst() + e.getSecond();
} else if (heightDiameter.getFirst() + e.getSecond() > height[1]) {
height[1] = heightDiameter.getFirst() + e.getSecond();
}
diameter = Math.max(diameter, heightDiameter.getSecond());
}
return new Pair<>(height[0], Math.max(diameter, height[0]
+ height[1]));
}

http://www.geeksforgeeks.org/diameter-n-ary-tree/
The diameter of an N-ary tree is the longest path present between any two nodes of the tree. These two nodes must be two leaf nodes.

The path can either start from one of the node and goes up to one of the LCAs of these nodes and again come down to the deepest node of some other subtree or can exist as a diameter of one of the child of the current node.
The solution will exist in any one of these:
I] Diameter of one of the children of the current node
II] Sum of Height of highest two subtree + 1

We can make a hash table to store heights of all nodes. If we precompute these heights, we don’t need to call depthOfTree() for every node.

int depthOfTree(struct Node *ptr)

{

    // Base case

    if (!ptr)

        return 0;

    int maxdepth = 0;

    // Check for all children and find

    // the maximum depth

    for (vector<Node*>::iterator it = ptr->child.begin();

                           it != ptr->child.end(); it++)

        maxdepth = max(maxdepth , depthOfTree(*it));

    return maxdepth + 1;

}

// Function to calculate the diameter

// of the tree

int diameter(struct Node *ptr)

{

    // Base case

    if (!ptr)

        return 0;

    // Find top two highest children

    int max1 = 0, max2 = 0;

    for (vector<Node*>::iterator it = ptr->child.begin();

                          it != ptr->child.end(); it++)

{

        int h = depthOfTree(*it);

        if (h > max1)

           max2 = max1, max1 = h;

        else if (h > max2)

           max2 = h;

}

    // Iterate over each child for diameter

    int maxChildDia = 0;

    for (vector<Node*>::iterator it = ptr->child.begin();

                           it != ptr->child.end(); it++)

        maxChildDia = max(maxChildDia, diameter(*it));

    return max(maxChildDia, max1 + max2 + 1);

}

https://discuss.leetcode.com/topic/83653/java-easy-to-understand-solution

this solution is intuitive but the performance is not good because of the overlapping subproblems when calculate depth.

diameterOfBinaryTree is called on every node. In each call, it traverses all descendants of that node to get the depth.

for root node, it is n => n + 1 - 2^0
for all nodes on 2nd level, it is 2 * (n - 1) / 2 => n - 1 => n + 1 - 2^1
for all nodes on 3rd level, it is 4 * (n - 3) / 4 => n - 3 => n + 1 - 2^2
for all nodes on 4th level, it is 8 * (n - 7) / 8 => n - 7 => n + 1 - 2^3
...
for all nodes on last level, it is n + 1 - 2^(h-1). h is max tree depth.

Add them up, the result is (n+1) * h - (1 + 2 + 4 ... + 2^(h-1)). In worst case, the latter part is n (all nodes in the tree), so time complexity is O(n*logn).

    public int diameterOfBinaryTree(TreeNode root) {
        if(root == null){
            return 0;
        }
       int dia = depth(root.left) + depth(root.right);
       int ldia = diameterOfBinaryTree(root.left);
       int rdia = diameterOfBinaryTree(root.right);
       return Math.max(dia,Math.max(ldia,rdia));
        
    }
    public int depth(TreeNode root){
        if(root == null){
            return 0;
        }
        return 1+Math.max(depth(root.left), depth(root.right));
    }

Longest path in an undirected tree
http://www.geeksforgeeks.org/longest-path-undirected-tree/
Given an undirected tree, we need to find the longest path of this tree where a path is defined as a sequence of nodes.
This problem is same as diameter of n-ary tree.

In this post, an efficient solution is discussed. We can find longest path using two BFSs. The idea is based on the following fact: If we start BFS from any node x and find a node with the longest distance from x, it must be an end point of the longest path. It can be proved using contradiction. So our algorithm reduces to simple two BFSs. First BFS to find an end point of the longest path and second BFS from this end point to find the actual longest path.
As we can see in above diagram, if we start our BFS from node-0, the node at the farthest distance from it will be node-5, now if we start our BFS from node-5 the node at the farthest distance will be node-7, finally, path from node-5 to node-7 will constitute our longest path.

pair<int, int> Graph::bfs(int u)

{

    //  mark all distance with -1

    int dis[V];

    memset(dis, -1, sizeof(dis));

    queue<int> q;

    q.push(u);

    //  distance of u from u will be 0

    dis[u] = 0;

    while (!q.empty())

{

        int t = q.front();       q.pop();

        //  loop for all adjacent nodes of node-t

        for (auto it = adj[t].begin(); it != adj[t].end(); it++)

{

            int v = *it;

            // push node into queue only if

            // it is not visited already

            if (dis[v] == -1)

{

                q.push(v);

                // make distance of v, one more

                // than distance of t

                dis[v] = dis[t] + 1;

}

}

}

    int maxDis = 0;

    int nodeIdx;

    //  get farthest node distance and its index

    for (int i = 0; i < V; i++)

{

        if (dis[i] > maxDis)

{

            maxDis = dis[i];

            nodeIdx = i;

}

}

    return make_pair(nodeIdx, maxDis);

}

//  method prints longest path of given tree

void Graph::longestPathLength()

{

    pair<int, int> t1, t2;

    // first bfs to find one end point of

    // longest path

    t1 = bfs(0);

    //  second bfs to find actual longest path

    t2 = bfs(t1.first);

    cout << "Longest path is from " << t1.first << " to "

         << t2.first << " of length " << t2.second;

}

O(N^2)
http://algorithms.tutorialhorizon.com/diameter-of-a-binary-tree/
https://algorithm.yuanbin.me/zh-hans/binary_tree/diameter_of_a_binary_tree.html

    public int diameter(TreeNode root) {
        if (root == null) return 0;

        // left, right height
        int leftHight = getHeight(root.left);
        int rightHight = getHeight(root.right);

        // left, right subtree diameter
        int leftDia = diameter(root.left);
        int rightDia = diameter(root.right);

        int maxSubDia = Math.max(leftDia, rightDia);
        return Math.max(maxSubDia, leftHight + 1 + rightHight);
    }

    private int getHeight(TreeNode root) {
        if (root == null) return 0;

        return 1 + Math.max(getHeight(root.left), getHeight(root.right));
    }

http://www.cnblogs.com/EdwardLiu/p/6404104.html
Find Longest Path in a Multi-Tree

给的多叉树, 找这颗树里面最长的路径长度

解法就是在子树里面找最大的两个（或一个，如果只有一个子树的话）高度加起来。

对于每一个treenode, 维护它的最高的高度和第二高的高度，经过该点的最大路径就是：最高高度+第二高高度，然后return 最高高度

 5 class TreeNode {
 6     int val;
 7     List<TreeNode> children;
 8     public TreeNode(int value) {
 9         this.val = value;
10         this.children = new ArrayList<TreeNode>();
11     }
12 }
13 
14 
15 public class LongestPathInTree {
16     static int maxLen = 0;
17     
18     public static int findLongestPath(TreeNode node) {
19         findMaxPath(node);
20         return maxLen;
21     }
22     
23     public static int findMaxPath(TreeNode node) {
24         if (node == null) return 0;
25         int heightest1 = 0;
26         int heightest2 = 0;
27         
28         for (TreeNode child : node.children) {
29             int childHeight = findMaxPath(child);
30             
31             if (childHeight > heightest1) {
32                 heightest2 = heightest1;
33                 heightest1 = childHeight;
34             }
35             else if (childHeight > heightest2) {
36                 heightest2 = childHeight;
37             }
38         }
39         maxLen = Math.max(maxLen, 1 + heightest1 + heightest2);
40         return 1 + heightest1;
41     }

http://wxx5433.github.io/tree-longest-path.html

https://www.geeksforgeeks.org/print-longest-leaf-leaf-path-binary-tree/
Print the longest leaf to leaf path in a Binary tree

We know that Diameter of a tree can be calculated by only using the height function because the diameter of a tree is nothing but the maximum value of (left_height + right_height + 1) for each node.
Now for the node which has the maximum value of (left_height + right_height + 1), we find the longest root to leaf path on the left side and similarly on the right side. Finally, we print left side path, root and right side path.

// Function to find height of a tree

int height(Node* root, int& ans, Node*(&k), int& lh, int& rh, 

                                                     int& f)

{

    if (root == NULL)

        return 0;

    int left_height = height(root->left, ans, k, lh, rh, f);

    int right_height = height(root->right, ans, k, lh, rh, f);

    // update the answer, because diameter of a

    // tree is nothing but maximum value of

    // (left_height + right_height + 1) for each node

    if (ans < 1 + left_height + right_height) {

        ans = 1 + left_height + right_height;

        // save the root, this will help us finding the

        //  left and the right part of the diameter

        k = root;

        // save the height of left & right subtree as well.

        lh = left_height;

        rh = right_height;

}

    return 1 + max(left_height, right_height);

}

// prints the root to leaf path

void printArray(int ints[], int len, int f)

{

    int i;

    // print left part of the path in reverse order

    if (f == 0) {

        for (i = len - 1; i >= 0; i--) {

            printf("%d ", ints[i]);

}

}

    // print right part of the path

    else if (f == 1) {

        for (i = 0; i < len; i++) {

            printf("%d ", ints[i]);

}

}

}

// this function finds out all the root to leaf paths

void printPathsRecur(Node* node, int path[], int pathLen, 

                                         int max, int& f)

{

    if (node == NULL)

        return;

    // append this node to the path array

    path[pathLen] = node->data;

    pathLen++;

    // If it's a leaf, so print the path that led to here

    if (node->left == NULL && node->right == NULL) {

        // print only one path which is equal to the 

        // height of the tree.

        if (pathLen == max && (f == 0 || f == 1)) {

            printArray(path, pathLen, f);

            f = 2;

}

}

    else {

        // otherwise try both subtrees

        printPathsRecur(node->left, path, pathLen, max, f);

        printPathsRecur(node->right, path, pathLen, max, f);

}

}

// Computes the diameter of a binary tree with given root.

void diameter(Node* root)

{

    if (root == NULL)

        return;

    // lh will store height of left subtree

    // rh will store height of right subtree

    int ans = INT_MIN, lh = 0, rh = 0;

    // f is a flag whose value helps in printing

    // left & right part of the diameter only once

    int f = 0;

    Node* k;

    int height_of_tree = height(root, ans, k, lh, rh, f);

    int lPath[100], pathlen = 0;

    // print the left part of the diameter

    printPathsRecur(k->left, lPath, pathlen, lh, f);

    printf("%d ", k->data);

    int rPath[100];

    f = 1;

    // print the right part of the diameter

    printPathsRecur(k->right, rPath, pathlen, rh, f);

}

https://github.com/mintycc/OnlineJudge-Solutions/blob/master/Leetcode/543_Diameter_of_Binary_Tree.java
https://github.com/mintycc/OnlineJudge-Solutions/blob/master/untag/Diameter%20of%20General%20Tree/DiameterOfTree.java

    public class TreeNode {
        int val;
        TreeNode[] children;
        TreeNode(int x, int n) { 
            val = x;
            children = new TreeNode[n];
        }
    }

    public int findDiameter(TreeNode root) {
        if (root == null) return 0;
        helper(root);
        return diameter;
    }

    int diameter = Integer.MIN_VALUE;

    private int helper(TreeNode root) {
        int a = Integer.MIN_VALUE;
        int b = Integer.MIN_VALUE;
        for (TreeNode child : root.children) {
            if (child == null) continue;
            int tmp = helper(child);
            if (tmp > a) { b = a; a = tmp;}
            else if (tmp > b) b = tmp;
        }

        if (b >= 0) diameter = Math.max(diameter, a + b + 2);
        if (a >= 0) {
            diameter = Math.max(diameter, a + 1);
            return a + 1;
        }
        return 0;
    }

1. ⻓长度的定义是边的个数，不不是node的个数
2. Follow-up: find the longest path in a normal tree (multiple children)

LeetCode 543 - Diameter of a Binary Tree

Compute the diameter of a generic tree - not a binary tree

Labels

Popular Posts