LeetCode 753 - Cracking the Safe

https://leetcode.com/problems/cracking-the-safe/

There is a box protected by a password. The password is n digits, where each letter can be one of the first k digits 0, 1, ..., k-1.

You can keep inputting the password, the password will automatically be matched against the last n digits entered.

For example, assuming the password is "345", I can open it when I type "012345", but I enter a total of 6 digits.

Please return any string of minimum length that is guaranteed to open the box after the entire string is inputted.

Example 1:

Input: n = 1, k = 2
Output: "01"
Note: "10" will be accepted too.

Example 2:

Input: n = 2, k = 2
Output: "00110"
Note: "01100", "10011", "11001" will be accepted too.

Note:

1. n will be in the range [1, 4].
2. k will be in the range [1, 10].
3. k^n will be at most 4096.

X.
https://leetcode.com/articles/cracking-the-safe/

• Time Complexity: $O(n * k^n)$. We visit every edge once in our depth-first search, and nodes take $O(n)$ space.
• Space Complexity: $O(n * k^n)$, the size of seen.

  Set<String> seen;

  StringBuilder ans;

  public String crackSafe(int n, int k) {

    if (n == 1 && k == 1)

      return "0";

    seen = new HashSet();

    ans = new StringBuilder();

    StringBuilder sb = new StringBuilder();

    for (int i = 0; i < n - 1; ++i)

      sb.append("0");

    String start = sb.toString();

    dfs(start, k);

    ans.append(start);

    return new String(ans);

  }

  public void dfs(String node, int k) {

    for (int x = 0; x < k; ++x) {

      String nei = node + x;

      if (!seen.contains(nei)) {

        seen.add(nei);

        dfs(nei.substring(1), k);

        ans.append(x);

      }

    }

  }

http://www.cnblogs.com/grandyang/p/8452361.html

这道题说的是给了k个数字，值为0到k-1，让我们组成n位密码。让我们找一个万能钥匙串，能破解任意的n位密码组合，这里对于破解的定义为只要密码是钥匙串的子串就可以破解了，然我们求出最短的一个万能钥匙串。来看一个例子，n=2，k=2，那么密码的组合有四种，

00，01，10，11

所以 00110 就是一种钥匙串，因为密码 00 (00110), 01 (00110), 10 (00110), 11 (00110), 分别都包括在钥匙串中。我们可以发现，为了尽可能的使钥匙串变短，所以我们的密码之间尽可能要相互重叠，比如00和01，就共享一个0，如果是3个数，012和120共享两个数"12"，那么我们可以发现，两个长度为n的密码最好能共享n-1个数字，这样累加出来的钥匙串肯定是最短的。

密码共有n位，每一个位可以有k个数字，那么总共不同的密码总数就有k的n次方个。我们的思路是先从n位都是0的密码开始，取出钥匙串的最后n个数字，然后将最后一个数字依次换成其他数字，我们用一个HashSet来记录所有遍历过的密码，这样如果不在集合中，说明是一个新密码，而生成这个新密码也只是多加了一个数字，这样能保证我们的钥匙串最短，这是一种贪婪的解法，相当的巧妙

    string crackSafe(int n, int k) {
        string res = string(n, '0');
        unordered_set<string> visited{{res}};
        for (int i = 0; i < pow(k, n); ++i) {
            string pre = res.substr(res.size() - n + 1, n - 1);
            for (int j = k - 1; j >= 0; --j) {
                string cur = pre + to_string(j);
                if (!visited.count(cur)) {
                    visited.insert(cur);
                    res += to_string(j);
                    break;
                }
            }
        }
        return res;
    }

https://leetcode.com/problems/cracking-the-safe/discuss/110264/Easy-DFS

This is kinda greedy approach.
So straight up we can tell that we have k^n combinations of the lock.
So the best way to generate the string is reusing last n-1 digits of previous lock << I can't really prove this but I realized this after writing down some examples.

Hence, we'll use dfs to generate the string with goal is when our string contains all possible combinations.

    public String crackSafe(int n, int k) {
        StringBuilder sb = new StringBuilder();
        int total = (int) (Math.pow(k, n));
        for (int i = 0; i < n; i++) sb.append('0');

        Set<String> visited = new HashSet<>();
        visited.add(sb.toString());

        dfs(sb, total, visited, n, k);

        return sb.toString();
    }

    private boolean dfs(StringBuilder sb, int goal, Set<String> visited, int n, int k) {
        if (visited.size() == goal) return true;
        String prev = sb.substring(sb.length() - n + 1, sb.length());
        for (int i = 0; i < k; i++) {
            String next = prev + i;
            if (!visited.contains(next)) {
                visited.add(next);
                sb.append(i);
                if (dfs(sb, goal, visited, n, k)) return true;
                else {
                    visited.remove(next);
                    sb.delete(sb.length() - 1, sb.length());
                }
            }
        }
        return false;
    }

https://leetcode.com/problems/cracking-the-safe/discuss/153039/DFS-with-Explanations

In order to guarantee to open the box at last, the input password ought to contain all length-n combinations on digits [0..k-1] - there should be k^n combinations in total.

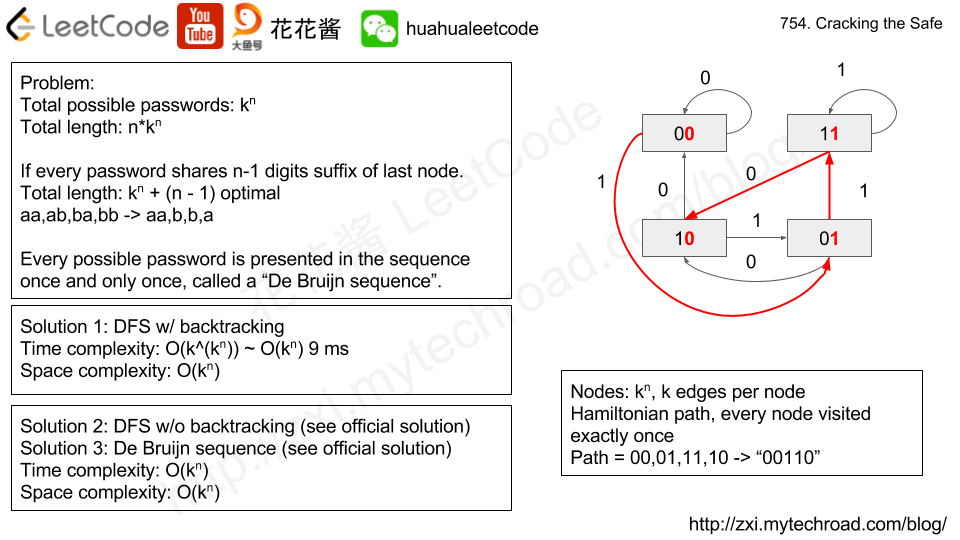
To make the input password as short as possible, we'd better make each possible length-n combination on digits [0..k-1] occurs exactly once as a substring of the password. The existence of such a password is proved by De Bruijn sequence:

A de Bruijn sequence of order n on a size-k alphabet A is a cyclic sequence in which every possible length-n string on A occurs exactly once as a substring. It has length k^n, which is also the number of distinct substrings of length n on a size-k alphabet; de Bruijn sequences are therefore optimally short.

We reuse last n-1 digits of the input-so-far password as below:

e.g., n = 2, k = 2
all 2-length combinations on [0, 1]: 
00 (`00`110), 
 01 (0`01`10), 
  11 (00`11`0), 
   10 (001`10`)
   
the password is 00110

We can utilize DFS to find the password:

goal: to find the shortest input password such that each possible n-length combination of digits [0..k-1] occurs exactly once as a substring.

node: current input password

edge: if the last n - 1 digits of node1 can be transformed to node2 by appending a digit from 0..k-1, there will be an edge between node1 and node2

start node: n repeated 0's
end node: all n-length combinations among digits 0..k-1 are visited

visitedComb: all combinations that have been visited

---

    public String crackSafe(int n, int k) {
        // Initialize pwd to n repeated 0's as the start node of DFS.
        String strPwd = String.join("", Collections.nCopies(n, "0"));
        StringBuilder sbPwd = new StringBuilder(strPwd);
        
        Set<String> visitedComb = new HashSet<>();
        visitedComb.add(strPwd);
    
        int targetNumVisited = (int) Math.pow(k, n);
        
        crackSafeAfter(sbPwd, visitedComb, targetNumVisited, n, k);
        
        return sbPwd.toString();
    }
    
    private boolean crackSafeAfter(StringBuilder pwd, Set<String> visitedComb, int targetNumVisited, int n, int k) {
        // Base case: all n-length combinations among digits 0..k-1 are visited. 
        if (visitedComb.size() == targetNumVisited) {
            return true;
        }
        
        String lastDigits = pwd.substring(pwd.length() - n + 1); // Last n-1 digits of pwd.
        for (char ch = '0'; ch < '0' + k; ch++) {
            String newComb = lastDigits + ch;
            if (!visitedComb.contains(newComb))  {
                visitedComb.add(newComb);
                pwd.append(ch);
                if (crackSafeAfter(pwd, visitedComb, targetNumVisited, n, k)) {
                    return true;
                }
                visitedComb.remove(newComb);
                pwd.deleteCharAt(pwd.length() - 1);
            }
        }
        
        return false;
    }

X. 

X. Approach #2: Inverse Burrows-Wheeler Transform [Accepted]

If we are familiar with the theory of combinatorics on words, recall that a Lyndon Word L is a word that is the unique minimum of it's rotations.

One important mathematical result (due to Fredericksen and Maiorana), is that the concatenation in lexicographic order of Lyndon words with length dividing n, forms a de Bruijin sequence: a sequence where every every word (from the $k^n$ available) appears as a substring of length n (where we are allowed to wrap around.)

For example, when n = 6, k = 2, all the Lyndon words with length dividing n in lexicographic order are (spaces for convenience): 0 000001 000011 000101 000111 001 001011 001101 001111 01 010111 011 011111 1. It turns out this is the smallest de Bruijin sequence.

We can use the Inverse Burrows-Wheeler Transform (IBWT) to generate these Lyndon words. Consider two sequences: S is the alphabet repeated $k^{n-1}$ times: S = 0123...0123...0123...., and S' is the alphabet repeated $k^{n-1}$ times for each letter: S' = 00...0011...1122.... We can think of S' and Sas defining a permutation, where the j-th occurrence of each letter of the alphabet in S' maps to the corresponding j-th occurrence in S. The cycles of this permutation turn out to be the corresponding smallest de Bruijin sequence (link).

Under this view, the permutation $S' \rightarrow S$ [mapping permutation indices $(i * k^{n-1} + q) \rightarrow (q * k + i)$] form the desired Lyndon words.

• Time Complexity: $O(k^n)$. We loop through every possible substring.
• Space Complexity: $O(k^n)$, the size of P and ans.

  public String crackSafe(int n, int k) {

    int M = (int) Math.pow(k, n - 1);

    int[] P = new int[M * k];

    for (int i = 0; i < k; ++i)

      for (int q = 0; q < M; ++q)

        P[i * M + q] = q * k + i;

    StringBuilder ans = new StringBuilder();

    for (int i = 0; i < M * k; ++i) {

      int j = i;

      while (P[j] >= 0) {

        ans.append(String.valueOf(j / M));

        int v = P[j];

        P[j] = -1;

        j = v;

      }

    }

    for (int i = 0; i < n - 1; ++i)

      ans.append("0");

    return new String(ans);

  }

    string crackSafe(int n, int k) {

        const int total_len = pow(k, n) + n - 1;        

        string node(n - 1, '0');

        string ans;

        unordered_set<string> visited;

        dfs(node, k, visited, ans);

        return ans + node;

    }

private:

    void dfs(const string& node, const int k, unordered_set<string>& visited, string& ans) {        

        for (char c = '0'; c < '0' + k; ++c) {

            string next = node + c;            

            if (visited.count(next)) continue;            

            visited.insert(next);                

            dfs(next.substr(1), k, visited, ans);

            ans.push_back(c);

        }

    }