LeetCode 1020 - Number of Enclaves

https://leetcode.com/problems/number-of-enclaves/

Given a 2D array A, each cell is 0 (representing sea) or 1 (representing land)

A move consists of walking from one land square 4-directionally to another land square, or off the boundary of the grid.

Return the number of land squares in the grid for which we cannot walk off the boundary of the grid in any number of moves.

Example 1:

Input: [[0,0,0,0],[1,0,1,0],[0,1,1,0],[0,0,0,0]]
Output: 3
Explanation: 
There are three 1s that are enclosed by 0s, and one 1 that isn't enclosed because its on the boundary.

Example 2:

Input: [[0,1,1,0],[0,0,1,0],[0,0,1,0],[0,0,0,0]]
Output: 0
Explanation: 
All 1s are either on the boundary or can reach the boundary.

Note:

1. 1 <= A.length <= 500
2. 1 <= A[i].length <= 500
3. 0 <= A[i][j] <= 1
4. All rows have the same size

https://leetcode.com/problems/number-of-enclaves/discuss/265555/C%2B%2B-with-picture-DFS-and-BFS

We flood-fill the land (change 1 to 0) from the boundary of the grid. Then, we count the remaining land.

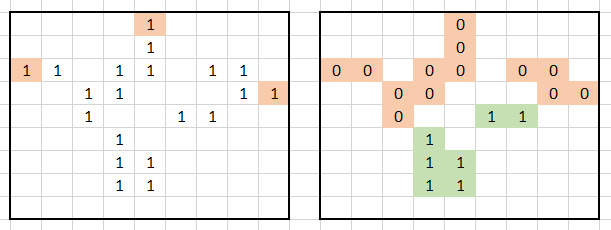
DFS Solution

The first cycle does DFS for the boundary cells. The second cycle counts the remaining land.

void dfs(vector<vector<int>>& A, int i, int j) {
  if (i < 0 || j < 0 || i == A.size() || j == A[i].size() || A[i][j] != 1) return;
  A[i][j] = 0;
  dfs(A, i + 1, j), dfs(A, i - 1, j), dfs(A, i, j + 1), dfs(A, i, j - 1);
}
int numEnclaves(vector<vector<int>>& A) {
  for (auto i = 0; i < A.size(); ++i)
    for (auto j = 0; j < A[0].size(); ++j) 
      if (i * j == 0 || i == A.size() - 1 || j == A[i].size() - 1) dfs(A, i, j);

  return accumulate(begin(A), end(A), 0, [](int s, vector<int> &r)
    { return s + accumulate(begin(r), end(r), 0); });
}

BFS Solution

Alternativelly, we can use a queue to implement BFS solution. For this problem, I don't think it's matter whether we do DFS or BFS. The runtime of the both solution is almost the same as well.

int numEnclaves(vector<vector<int>>& A, int res = 0) {
  queue<pair<int, int>> q;
  for (auto i = 0; i < A.size(); ++i)
    for (auto j = 0; j < A[0].size(); ++j) {
      res += A[i][j];
      if (i * j == 0 || i == A.size() - 1 || j == A[i].size() - 1) q.push({ i, j });
    }
  while (!q.empty()) {
    auto x = q.front().first, y = q.front().second; q.pop();
    if (x < 0 || y < 0 || x == A.size() || y == A[x].size() || A[x][y] != 1) continue;
    A[x][y] = 0;
    --res;
    q.push({ x + 1, y }), q.push({ x - 1, y }), q.push({ x, y + 1 }), q.push({ x, y - 1 });
  }
  return res;
}

https://leetcode.com/problems/number-of-enclaves/discuss/265699/Detailed-Explanation-using-Connected-Components

    int ROW, COL;
public:
    int numEnclaves(vector<vector<int>>& a);
    void dfs(vector<vector<int>>& a, int i, int j);
};

void Solution :: dfs(vector<vector<int>>& a, int i, int j)
{
    if(i<0 || i>=ROW || j<0 || j>=COL) return;
    if(a[i][j]==0 || a[i][j]==-1) return;
 
    a[i][j] = -1;
    
    dfs(a,i-1,j); dfs(a,i+1,j);
    dfs(a,i,j-1); dfs(a,i,j+1);
}

int Solution :: numEnclaves(vector<vector<int>>& a)
{
    ROW = a.size();
    COL = a[0].size();
    
    vector<int> rowBorders = {0,ROW-1};
    vector<int> colBorders = {0,COL-1};
    
    for(int i : rowBorders)
        for(int j=0; j<COL; j++)
            dfs(a,i,j);
    
    for(int j : colBorders)
        for(int i=0; i<ROW; i++)
            dfs(a,i,j);
    
    int count=0;
    for(auto &row_vec:a)
        for(auto &ele : row_vec)
            if(ele==1) count++;
    
    return count;
    
}