Expression Add Operators | LeetCode OJ
Given a string that contains only digits
Examples:
http://www.cnblogs.com/grandyang/p/4814506.html
https://github.com/mintycc/OnlineJudge-Solutions/blob/master/Leetcode/282_Expression_Add_Operators.java
https://zxi.mytechroad.com/blog/searching/leetcode-282-expression-add-operators/
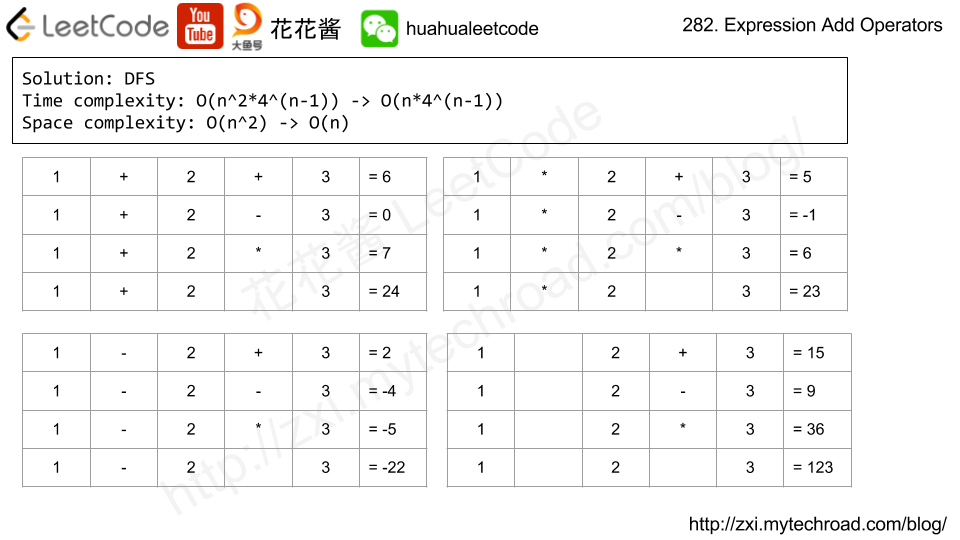
Time complexity: O(4^n)
Space complexity: O(n^2) -> O(n)
X. DFS
Time complexity:
https://leetcode.com/discuss/58614/java-standard-backtrace-ac-solutoin-short-and-clear
https://leetcode.com/discuss/83759/java-ac-solution-19ms-beat-100-00%25
void dfs(List<String> ret, char[] path, int len, long left, long cur, char[] digits, int pos, int target) {
if (pos == digits.length) {
if (left + cur == target) ret.add(new String(path, 0, len));
return;
}
long n = 0;
int j = len + 1;
for (int i = pos; i < digits.length; i++) {
n = n * 10 + digits[i] - '0';
path[j++] = digits[i];
path[len] = '+';
dfs(ret, path, j, left + cur, n, digits, i + 1, target);
path[len] = '-';
dfs(ret, path, j, left + cur, -n, digits, i + 1, target);
path[len] = '*';
dfs(ret, path, j, left, cur * n, digits, i + 1, target);
if (digits[pos] == '0') break;
}
}
public List<String> addOperators(String num, int target) {
List<String> ret = new LinkedList<>();
if (num.length() == 0) return ret;
char[] path = new char[num.length() * 2 - 1];
char[] digits = num.toCharArray();
long n = 0;
for (int i = 0; i < digits.length; i++) {
n = n * 10 + digits[i] - '0';
path[i] = digits[i];
dfs(ret, path, i + 1, 0, n, digits, i + 1, target);
if (n == 0) break;
}
return ret;
}
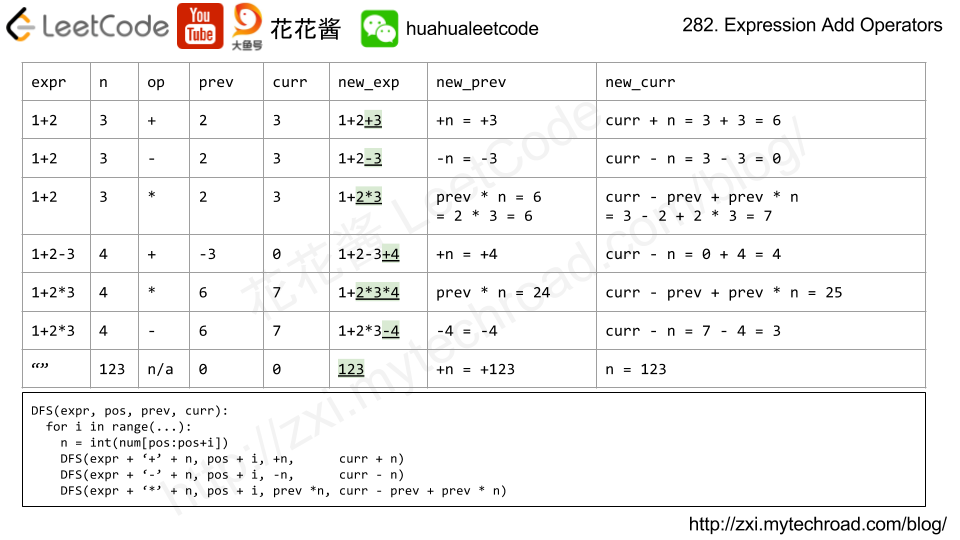
因为要输出所有可能的情况,必定是用深度优先搜索。问题在于如何将问题拆分成多次搜索。加减法很好处理,每当我们截出一段数字时,将之前计算的结果加上或者减去这个数,就可以将剩余的数字字符串和新的计算结果代入下一次搜索中了,直到我们的计算结果和目标一样,就完成了一次搜索。然而,乘法如何处理呢?这里我们需要用一个变量记录乘法当前累乘的值,直到累乘完了,遇到下一个加号或减号再将其算入计算结果中。这里有两种情况:
http://blog.csdn.net/u013027996/article/details/48713751
http://shibaili.blogspot.com/2015/09/day-130-286-expression-add-operators.html
#1 这种for循环内的写法可以简化没有符合时的情况
如1234
1 _ 234
12_34
123_4
1234
-----------
from 1_234:
1_2_34
1_23_4
1_234
........
如果遇到“*”,则返回之前的操作(因为之前的运算符和值都已经存好)
1 + 2 * 3,之前 1 + 2已经算出为3,之前的运算符为+,值为2。然后此时 总值- 2 + 2 * 3
cur为当前的总值,op为之前运算符,val为上一步计算的值
http://likemyblogger.blogspot.com/2015/09/leetcode-282-expression-add-operators.html
Given a string that contains only digits
0-9 and a target value, return all possibilities to add binary operators (not unary) +, -, or * between the digits so they evaluate to the target value. Examples:
"123", 6 -> ["1+2+3", "1*2*3"]
"232", 8 -> ["2*3+2", "2+3*2"]
"105", 5 -> ["1*0+5","10-5"]
"00", 0 -> ["0+0", "0-0", "0*0"]
"3456237490", 9191 -> []
http://www.cnblogs.com/grandyang/p/4814506.html
这道题给了我们一个只由数字组成的字符串,让我们再其中添加+,-或*号来形成一个表达式,该表达式的计算和为给定了target值,让我们找出所有符合要求的表达式来。看了题目中的例子1和2,很容易让人误以为是必须拆成个位数字,其实不是的,比如例子3中的 "105", 5能返回"10-5",说明连着的数字也可以。如果非要在过往的题中找一道相似的题,我觉得跟 Combination Sum II 很类似。不过这道题要更复杂麻烦一些。还是用递归来解题,我们需要两个变量diff和curNum,一个用来记录将要变化的值,另一个是当前运算后的值,而且它们都需要用 long 型的,因为字符串转为int型很容易溢出,所以我们用长整型。对于加和减,diff就是即将要加上的数和即将要减去的数的负值,而对于乘来说稍有些复杂,此时的diff应该是上一次的变化的diff乘以即将要乘上的数,有点不好理解,那我们来举个例子,比如 2+3*2,即将要运算到乘以2的时候,上次循环的 curNum = 5, diff = 3, 而如果我们要算这个乘2的时候,新的变化值diff应为 3*2=6,而我们要把之前+3操作的结果去掉,再加上新的diff,即 (5-3)+6=8,即为新表达式 2+3*2 的值,有点难理解,大家自己一步一步推算吧。
还有一点需要注意的是,如果输入为"000",0的话,容易出现以下的错误:
Wrong:["0+0+0","0+0-0","0+0*0","0-0+0","0-0-0","0-0*0","0*0+0","0*0-0","0*0*0","0+00","0-00","0*00","00+0","00-0","00*0","000"]
Correct:["0*0*0","0*0+0","0*0-0","0+0*0","0+0+0","0+0-0","0-0*0","0-0+0","0-0-0"]
我们可以看到错误的结果中有0开头的字符串出现,明显这不是数字,所以我们要去掉这些情况,过滤方法也很简单,我们只要判断长度大于1且首字符是‘0’的字符串,将其滤去即可
https://github.com/mintycc/OnlineJudge-Solutions/blob/master/Leetcode/282_Expression_Add_Operators.java
public List<String> addOperators(String num, int target) {
List<String> ans = new ArrayList<String>();
search(0, 0, 0, target, new StringBuilder(), num, ans);
return ans;
}
private void search(int index, long last, long sum, int target, StringBuilder prefix, String s, List<String> ans) {
if (index == s.length()) {
if (sum == target)
ans.add(prefix.toString());
return;
}
int len = prefix.length();
long num = 0;
for (int i = index; i < s.length(); i ++) {
num = num * 10 + s.charAt(i) - '0';
if (index == 0) {
search(i + 1, num, num, target, prefix.append(num), s, ans);
prefix.setLength(len);
} else {
prefix.append('+'); prefix.append(num);
search(i + 1, num, sum + num, target, prefix, s, ans);
prefix.setLength(len);
prefix.append('-'); prefix.append(num);
search(i + 1, -num, sum - num, target, prefix, s, ans);
prefix.setLength(len);
prefix.append('*'); prefix.append(num);
search(i + 1, last * num, sum - last + last * num, target, prefix, s, ans);
prefix.setLength(len);
}
if (num == 0) break;
}
}
Time complexity: O(4^n)
Space complexity: O(n^2) -> O(n)
private List<String> ans;
private char[] num;
private char[] exp;
private int target;
public List<String> addOperators(String num, int target) {
this.num = num.toCharArray();
this.ans = new ArrayList<>();
this.target = target;
this.exp = new char[num.length() * 2];
dfs(0, 0, 0, 0);
return ans;
}
private void dfs(int pos, int len, long prev, long curr) {
if (pos == num.length) {
if (curr == target)
ans.add(new String(exp, 0, len));
return;
}
int s = pos;
int l = len;
if (s != 0) ++len;
long n = 0;
while (pos < num.length) {
if (num[s] == '0' && pos - s > 0) break; // 0X...
n = n * 10 + (int)(num[pos] - '0');
if (n > Integer.MAX_VALUE) break; // too long
exp[len++] = num[pos++]; // copy exp
if (s == 0) {
dfs(pos, len, n, n);
continue;
}
exp[l] = '+'; dfs(pos, len, n, curr + n);
exp[l] = '-'; dfs(pos, len, -n, curr - n);
exp[l] = '*'; dfs(pos, len, prev * n, curr - prev + prev * n);
}
}
Time complexity:
T(n) = 3 * T(n-1) + 3 * T(n-2) + 3 * T(n-3) + ... + 3 *T(1);
T(n-1) = 3 * T(n-2) + 3 * T(n-3) + ... 3 * T(1);
Thus T(n) = 4T(n-1);
So the time complexity is O(4^n)
https://leetcode.com/discuss/59557/what-is-the-best-time-complexity-of-this-problem
https://leetcode.com/discuss/59557/what-is-the-best-time-complexity-of-this-problem
for nums="0000..0", target=0 and you get the output consisting of 3^(n-1) strings.
One can construct other exponential cases, e.g. nums="AdddBddCdddd..dddd" with even number of d's and target=A+B+C. In this case you'll have at least a set of strings where all d's evaluate to 0 and doing this with only '+'s and '-'s between d's will be exponential.
On the other hand there are special cases that are solvable in O(N). E.g. nums consisting of only even digits and an odd target or if nums consists of 0,3,6,9 and target is not divisible by 3.
This problem has a lot of edge cases to be considered:
- overflow: we use a long type once it is larger than Integer.MAX_VALUE or minimum, we get over it.
- 0 sequence: because we can't have numbers with multiple digits started with zero, we have to deal with it too.
- a little trick is that we should save the value that is to be multiplied in the next recursion.
public List<String> addOperators(String num, int target) {
List<String> rst = new ArrayList<String>();
if(num == null || num.length() == 0) return rst;
helper(rst, "", num, target, 0, 0, 0);
return rst;
}
public void helper(List<String> rst, String path, String num, int target, int pos, long eval, long multed){
if(pos == num.length()){
if(target == eval)
rst.add(path);
return;
}
for(int i = pos; i < num.length(); i++){
if(i != pos && num.charAt(pos) == '0') break;
long cur = Long.parseLong(num.substring(pos, i + 1));
if(pos == 0){
helper(rst, path + cur, num, target, i + 1, cur, cur);
}
else{
helper(rst, path + "+" + cur, num, target, i + 1, eval + cur , cur);
helper(rst, path + "-" + cur, num, target, i + 1, eval -cur, -cur);
helper(rst, path + "*" + cur, num, target, i + 1, eval - multed + multed * cur, multed * cur );
}
}
}
However, adding String is extremely expensive. Speed can be increased by
20% if you useStringBuilderinstead.
Before:
public List<String> addOperators(String num, int target) {
List<String> res = new ArrayList<>();
StringBuilder sb = new StringBuilder();
dfs(res, sb, num, 0, target, 0, 0);
return res;
}
public void dfs(List<String> res, StringBuilder sb, String num, int pos, int target, long prev, long multi) {
if(pos == num.length()) {
if(target == prev) res.add(sb.toString());
return;
}
for(int i = pos; i < num.length(); i++) {
if(num.charAt(pos) == '0' && i != pos) break;
long curr = Long.parseLong(num.substring(pos, i + 1));//curr=curee*10+currentValue
int len = sb.length();
if(pos == 0) {
dfs(res, sb.append(curr), num, i + 1, target, curr, curr);
sb.setLength(len);
} else {
dfs(res, sb.append("+").append(curr), num, i + 1, target, prev + curr, curr);
sb.setLength(len);
dfs(res, sb.append("-").append(curr), num, i + 1, target, prev - curr, -curr);
sb.setLength(len);
dfs(res, sb.append("*").append(curr), num, i + 1, target, prev - multi + multi * curr, multi * curr);
sb.setLength(len);
}
}
}238ms (67.31%) Now: 189ms (96.56%)
A tiny thing is that when we get cur, I think we should check
if(cur > (long)Integer.MAX_VALUE) break; , since the input may cause long overflow whennum.substring(pos, i + 1) get longer (the OJ text cases do not contain such case though).
Both your solution and yanvinci's soultion are using substring, which will create a new String every time. The reason is that String is immutable in Java. Also, I use char[] num instead of String num, because if you are using the latter, everytime you get the char at a certain index, Java will do the range check for the index which is already checked in our code and is not necessary to check again!
public List<String> addOperators(String num, int target) { List<String> res = new ArrayList<>(); StringBuilder sb = new StringBuilder(); dfs(res, sb, num.toCharArray(), 0, target, 0, 0); return res; } public void dfs(List<String> res, StringBuilder sb, char[] num, int pos, int target, long prev, long multi) { if(pos == num.length) { if(target == prev) res.add(sb.toString()); return; } long curr = 0; for(int i = pos; i < num.length; i++) { if(num[pos] == '0' && i != pos) break; curr = 10 * curr + num[i] - '0'; int len = sb.length(); if(pos == 0) { dfs(res, sb.append(curr), num, i + 1, target, curr, curr); sb.setLength(len); } else { dfs(res, sb.append("+").append(curr), num, i + 1, target, prev + curr, curr); sb.setLength(len); dfs(res, sb.append("-").append(curr), num, i + 1, target, prev - curr, -curr); sb.setLength(len); dfs(res, sb.append("*").append(curr), num, i + 1, target, prev - multi + multi * curr, multi * curr); sb.setLength(len); } } }
the last line about multi and curr is great, a smart way to undo prev +/- operations and give priority to multiplication.
your avoidance of String/StringBuffer operation lets you outperform the previous solution 10x times.
I am also wondering whether it can be accelerated more by adding memorization.
http://segmentfault.com/a/1190000003797204因为要输出所有可能的情况,必定是用深度优先搜索。问题在于如何将问题拆分成多次搜索。加减法很好处理,每当我们截出一段数字时,将之前计算的结果加上或者减去这个数,就可以将剩余的数字字符串和新的计算结果代入下一次搜索中了,直到我们的计算结果和目标一样,就完成了一次搜索。然而,乘法如何处理呢?这里我们需要用一个变量记录乘法当前累乘的值,直到累乘完了,遇到下一个加号或减号再将其算入计算结果中。这里有两种情况:
- 乘号之前是加号或减号,例如
2+3*4,我们在2那里算出来的结果,到3的时候会加上3,计算结果变为5。在到4的时候,因为4之前我们选择的是乘号,这里3就应该和4相乘,而不是和2相加,所以在计算结果时,要将5先减去刚才加的3得到2,然后再加上3乘以4,得到2+12=14,这样14就是到4为止时的计算结果。 - 另外一种情况是乘号之前也是乘号,如果
2+3*4*5,这里我们到4为止计算的结果是14了,然后我们到5的时候又是乘号,这时候我们要把刚才加的3*4给去掉,然后再加上3*4*5,也就是14-3*4+3*4*5=62。这样5的计算结果就是62。
因为要解决上述几种情况,我们需要这么几个变量,一个是记录上次的计算结果
currRes,一个是记录上次被加或者被减的数prevNum,一个是当前准备处理的数currNum。当下一轮搜索是加减法时,prevNum就是简单换成currNum,当下一轮搜索是乘法时,prevNum是prevNum乘以currNum。- 第一次搜索不添加运算符,只添加数字,就不会出现
+1+2这种表达式了。 - 我们截出的数字不能包含0001这种前面有0的数字,但是一个0是可以的
List<String> res;
public List<String> addOperators(String num, int target) {
res = new ArrayList<String>();
helper(num, target, "", 0, 0);
return res;
}
private void helper(String num, int target, String tmp, long currRes, long prevNum){
// 如果计算结果等于目标值,且所有数都用完了,则是有效结果
if(currRes == target && num.length() == 0){
String exp = new String(tmp);// not needed
res.add(exp);
return;
}
// 搜索所有可能的拆分情况
for(int i = 1; i <= num.length(); i++){
String currStr = num.substring(0, i);
// 对于前导为0的数予以排除
if(currStr.length() > 1 && currStr.charAt(0) == '0'){
return;
}
// 得到当前截出的数
long currNum = Long.parseLong(currStr);
// 去掉当前的数,得到下一轮搜索用的字符串
String next = num.substring(i);
// 如果不是第一个字母时,可以加运算符,否则只加数字
if(tmp.length() != 0){
// 乘法
helper(next, target, tmp+"*"+currNum, (currRes - prevNum) + prevNum * currNum, prevNum * currNum);
// 加法
helper(next, target, tmp+"+"+currNum, currRes + currNum, currNum);
// 减法
helper(next, target, tmp+"-"+currNum, currRes - currNum, -currNum);
} else {
// 第一个数
helper(next, target, currStr, currNum, currNum);
}
}
} public List<String> addOperators(String num, int target) { List<String> result = new ArrayList<>(); if (num == null || num.length() == 0) { return result; } addOperatorHelper(num, 0, target, 0, 0, "", result); return result; } private void addOperatorHelper(String num, int start, int target, long curSum, long preNum, String curResult, List<String> result) { if (start == num.length() && curSum == target) { result.add(curResult); return; } if (start == num.length()) { return; } for (int i = start; i < num.length(); i++) { String curStr = num.substring(start, i + 1); if (curStr.length() > 1 && curStr.charAt(0) == '0') { break; } long curNum = Long.parseLong(curStr); if (curResult.isEmpty()) { addOperatorHelper(num, i + 1, target, curNum, curNum, curStr, result); } else { // Multiply addOperatorHelper(num, i + 1, target, curSum - preNum + preNum * curNum, preNum * curNum, curResult + "*" + curNum, result); // Add addOperatorHelper(num, i + 1, target, curSum + curNum, curNum, curResult + "+" + curNum, result); // Subtract addOperatorHelper(num, i + 1, target, curSum - curNum, -curNum, curResult + "-" + curNum, result); } } }http://blog.csdn.net/u013027996/article/details/48713751
http://shibaili.blogspot.com/2015/09/day-130-286-expression-add-operators.html
#1 这种for循环内的写法可以简化没有符合时的情况
如1234
1 _ 234
12_34
123_4
1234
-----------
from 1_234:
1_2_34
1_23_4
1_234
........
如果遇到“*”,则返回之前的操作(因为之前的运算符和值都已经存好)
1 + 2 * 3,之前 1 + 2已经算出为3,之前的运算符为+,值为2。然后此时 总值- 2 + 2 * 3
cur为当前的总值,op为之前运算符,val为上一步计算的值
class Solution {public: int target; void dfs(vector<string> &rt,string num,int index,string sofar,long cur,string op,long val) { if (index == num.length() && target == cur) { rt.push_back(sofar); } for (int i = index; i < num.length(); i++) { string s = num.substr(index,i + 1 - index); if (s != to_string(stol(s))) continue; int now = stol(s); dfs(rt,num,i + 1,sofar + "+" + s,cur + now,"+",now); dfs(rt,num,i + 1,sofar + "-" + s,cur - now,"-",now); if (op == "-") { dfs(rt,num,i + 1,sofar + "*" + s,cur + val - val * now,op,val * now); }else if (op == "+") { dfs(rt,num,i + 1,sofar + "*" + s,cur - val + val * now,op,val * now); }else { dfs(rt,num,i + 1,sofar + "*" + s,val * now,op,val * now); } } } vector<string> addOperators(string num, int target) { vector<string> rt; this->target = target; for (int i = 1; i <= num.length(); i++) { string s = num.substr(0,i); if (s != to_string(stol(s))) continue; dfs(rt,num,i,s,stol(s),"",stol(s)); } return rt; }};
DFS(深度优先搜索)
将字符串拆解成left + operator + right的形式,针对left执行递归
注意:包含前导0的运算数是无效的。
例如,通过"00+9"获得目标值9是不正确的。http://www.cnblogs.com/grandyang/p/4814506.html
http://techinpad.blogspot.com/2015/09/leetcode-expression-add-operators.html
http://likemyblogger.blogspot.com/2015/09/leetcode-282-expression-add-operators.html
http://bookshadow.com/weblog/2015/09/16/leetcode-expression-add-operators/
class Solution(object): def addOperators(self, num, target): """ :type num: str :type target: int :rtype: List[str] """ def isLeadingZeros(num): return num.startswith('00') or int(num) and num.startswith('0') def solve(num, target, mulExpr = '', mulVal = 1): ans = [] #remove leading zeros if isLeadingZeros(num): pass elif int(num) * mulVal == target: ans += num + mulExpr, for x in range(len(num) - 1): lnum, rnum = num[:x+1], num[x+1:] #remove leading zeros if isLeadingZeros(rnum): continue right, rightVal = rnum + mulExpr, int(rnum) * mulVal #op = '+' for left in solve(lnum, target - rightVal): ans += left + '+' + right, #op = '-' for left in solve(lnum, target + rightVal): ans += left + '-' + right, #op = '*' for left in solve(lnum, target, '*' + right, rightVal): ans += left, return ans if not num: return [] return solve(num, target)
X.
简化版:给⼀一个数字字符串串在中间任意位置加正负号使和等于target
https://github.com/mintycc/OnlineJudge-Solutions/blob/master/untag/Expression%20Add%20Operators%20Simple/ExpressionAddOperators.java
将字符串拆解成left + operator + right的形式,针对left执行递归
注意:包含前导0的运算数是无效的。
例如,通过"00+9"获得目标值9是不正确的。http://www.cnblogs.com/grandyang/p/4814506.html
还有一点需要注意的是,如果输入为"000",0的话,容易出现以下的错误:
Wrong:["0+0+0","0+0-0","0+0*0","0-0+0","0-0-0","0-0*0","0*0+0","0*0-0","0*0*0","0+00","0-00","0*00","00+0","00-0",
"00*0","000"]
Correct:["0*0*0","0*0+0","0*0-0","0+0*0","0+0+0","0+0-0","0-0*0","0-0+0","0-0-0"]
我们可以看到错误的结果中有0开头的字符串出现,明显这不是数字,所以我们要去掉这些情况,过滤方法也很简单,我们只要判断长度大于1且首字符是‘0’的字符串,将其滤去即可,参见代码如下:
def isLeadingZeros(num):
return num.startswith('00') or int(num) and num.startswith('0')
def solve(num, target, mulExpr = '', mulVal = 1):
ans = []
#remove leading zeros
if isLeadingZeros(num):
pass
elif int(num) * mulVal == target:
ans += num + mulExpr,
for x in range(len(num) - 1):
lnum, rnum = num[:x+1], num[x+1:]
#remove leading zeros
if isLeadingZeros(rnum):
continue
right, rightVal = rnum + mulExpr, int(rnum) * mulVal
#op = '+'
for left in solve(lnum, target - rightVal):
ans += left + '+' + right,
#op = '-'
for left in solve(lnum, target + rightVal):
ans += left + '-' + right,
#op = '*'
for left in solve(lnum, target, '*' + right, rightVal):
ans += left,
return ans
if not num:
return []
return solve(num, target)http://techinpad.blogspot.com/2015/09/leetcode-expression-add-operators.html
http://likemyblogger.blogspot.com/2015/09/leetcode-282-expression-add-operators.html
http://bookshadow.com/weblog/2015/09/16/leetcode-expression-add-operators/
class Solution(object): def addOperators(self, num, target): """ :type num: str :type target: int :rtype: List[str] """ def isLeadingZeros(num): return num.startswith('00') or int(num) and num.startswith('0') def solve(num, target, mulExpr = '', mulVal = 1): ans = [] #remove leading zeros if isLeadingZeros(num): pass elif int(num) * mulVal == target: ans += num + mulExpr, for x in range(len(num) - 1): lnum, rnum = num[:x+1], num[x+1:] #remove leading zeros if isLeadingZeros(rnum): continue right, rightVal = rnum + mulExpr, int(rnum) * mulVal #op = '+' for left in solve(lnum, target - rightVal): ans += left + '+' + right, #op = '-' for left in solve(lnum, target + rightVal): ans += left + '-' + right, #op = '*' for left in solve(lnum, target, '*' + right, rightVal): ans += left, return ans if not num: return [] return solve(num, target)
X.
简化版:给⼀一个数字字符串串在中间任意位置加正负号使和等于target
https://github.com/mintycc/OnlineJudge-Solutions/blob/master/untag/Expression%20Add%20Operators%20Simple/ExpressionAddOperators.java
public List<String> addOperators(String num, int target) {
List<String> ans = new ArrayList<String>();
search(0, 0, target, "", num, ans);
return ans;
}
private void search(int index, long sum, int target, String prefix, String s, List<String> ans) {
if (index == s.length()) {
if (sum == target)
ans.add(prefix);
return;
}
long num = 0;
for (int i = index; i < s.length(); i ++) {
num = num * 10 + s.charAt(i) - '0';
if (index == 0)
search(i + 1, num, target, "" + num, s, ans);//
else {
search(i + 1, sum + num, target, prefix + "+" + num, s, ans);
search(i + 1, sum - num, target, prefix + "-" + num, s, ans);
}
if (num == 0) break;
}
}