Isotonic Regression | Algorithms Notes
Given a sequence A of n integers, design an algorithm to find an non-decreasing sequence B of n integers, such that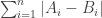 is minimized.
is minimized.
Solution:
This problem can be solved by minimum cost flow. Here we use dynamic programming.
Let F(k, z) be the optimal objective value for the first k elements with B[k] = z. Then, we have a recurrence relation: F(k, z) = min F(k-1, x) + |z – A[k]|. Thus, the problem becomes how to efficiently find the z minimizing F(k, z) for all fixed k. It can be showed that F(k, z) is a piecewise linear convex function in z and the minimizing value must be in A. Thus, the dynamic programming can be speed up by using slope optimization and find the solution in O(n lg n) time.
Read full article from Isotonic Regression | Algorithms Notes
Given a sequence A of n integers, design an algorithm to find an non-decreasing sequence B of n integers, such that
Solution:
This problem can be solved by minimum cost flow. Here we use dynamic programming.
Let F(k, z) be the optimal objective value for the first k elements with B[k] = z. Then, we have a recurrence relation: F(k, z) = min F(k-1, x) + |z – A[k]|. Thus, the problem becomes how to efficiently find the z minimizing F(k, z) for all fixed k. It can be showed that F(k, z) is a piecewise linear convex function in z and the minimizing value must be in A. Thus, the dynamic programming can be speed up by using slope optimization and find the solution in O(n lg n) time.
Read full article from Isotonic Regression | Algorithms Notes