http://javarevisited.blogspot.com/2014/05/how-to-find-prime-factors-of-integer-number-java.html
You are asked to write a program to find prime factors of given integer number. The prime factors of a number are all of the prime numbers that will exactly divide the given number. For example prime factors of 35 are 7 and 5, both are prime in itself and exactly divides 35
it's a simple brute-force logic to find prime factors. We start from 2, because that's the first prime number and every number is also divisible by 1, then we iterate until we find a prime factor by incrementing and stepping one at a time. When we find a prime factor, we store it inside a Set and also reduce the number till which we are looping.
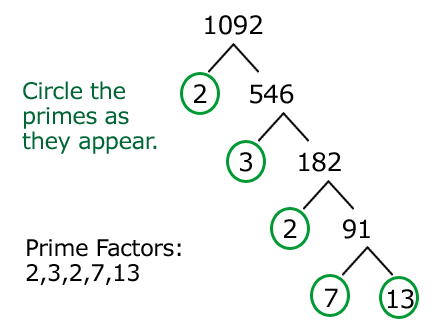
https://reeestart.wordpress.com/2016/06/23/google-all-prime-factors-of-n/
http://www.vogella.com/tutorials/JavaAlgorithmsPrimeFactorization/article.html
Performance optimized version
This uses the fact that if we now that a loop i n has no divisors less then or equal then i (which I have explained earlier) it can also not have a divisor which is larger then n/i.
Also http://introcs.cs.princeton.edu/java/13flow/Factors.java.html
http://www.geeksforgeeks.org/print-all-prime-factors-of-a-given-number/
Step 1 takes care of even numbers. And after step 1, all remaining prime factor must be odd (difference of two prime factors must be at least 2), this explains why i is incremented by 2.
Now the main part is, the loop runs till square root of n not till. To prove that this optimization works, let us consider the following property of composite numbers.
Every composite number has at least one prime factor less than or equal to square root of itself.
This property can be proved using counter statement. Let a and b be two factors of n such that a*b = n. If both are greater than √n, then a.b > √n, * √n, which contradicts the expression “a * b = n”.
A composite number is a positive integer that has at least one positive divisor other than one or the number itself. In other words, a composite number is any integer greater than one that is not a prime number.
https://www.quora.com/Which-is-the-fastest-prime-factorization-algorithm-to-date
http://introcs.cs.princeton.edu/java/78crypto/PollardRho.java.html
http://www.acmerblog.com/jiudu-1207-2363.html
九度-1207-质因数的个数[解题代码]
You are asked to write a program to find prime factors of given integer number. The prime factors of a number are all of the prime numbers that will exactly divide the given number. For example prime factors of 35 are 7 and 5, both are prime in itself and exactly divides 35
it's a simple brute-force logic to find prime factors. We start from 2, because that's the first prime number and every number is also divisible by 1, then we iterate until we find a prime factor by incrementing and stepping one at a time. When we find a prime factor, we store it inside a Set and also reduce the number till which we are looping.

https://reeestart.wordpress.com/2016/06/23/google-all-prime-factors-of-n/
给一个数n,找出它所有的prime factor
[Solution]
首先无论n是多少,得把2去掉,去掉之后n必然是一个奇数。
首先无论n是多少,得把2去掉,去掉之后n必然是一个奇数。
然后从3开始,一直到sqrt(n),挨个找prime factor,increment by 2,因为偶数不可能是prime number。
至于为什么到sqrt(n)就可以停止,可以这么来证明,假设a和b是n的prime factor,那么a * b = n,如果a和b都大于sqrt(n),那么他们的乘积必然大于n。
所以不可能有两个或两个以上的prime factor大于sqrt(n)的情况。
最后如果n本身就是一个prime number,需要把它自己加入到result list里。
public List<Integer> factors(int n) { List<Integer> result = new ArrayList<>(); Set<Integer> set = new HashSet<>(); while (n % 2 == 0) { if (!set.contains(2)) { result.add(2); set.add(2); } n /= 2; } for (int i = 3; i <= Math.sqrt(n); i += 2) { while (n % i == 0) { if (!set.contains(i)) { result.add(i); set.add(i); } n /= i; } } // if n is a prime number if (n > 2) { result.add(n); } return result; }public static List<Integer> primeFactors(int number) { int n = number; List<Integer> factors = new ArrayList<Integer>(); for (int i = 2; i <= n; i++) { while (n % i == 0) { factors.add(i); n /= i; } } return factors; }
Performance optimized version
This uses the fact that if we now that a loop i n has no divisors less then or equal then i (which I have explained earlier) it can also not have a divisor which is larger then n/i.
Also http://introcs.cs.princeton.edu/java/13flow/Factors.java.html
public static List<Integer> primeFactors(int numbers) { int n = numbers; List<Integer> factors = new ArrayList<Integer>(); for (int i = 2; i <= n / i; i++) { while (n % i == 0) { factors.add(i); n /= i; } } if (n > 1) { factors.add(n); } return factors; }More optimization: i+=2
http://www.geeksforgeeks.org/print-all-prime-factors-of-a-given-number/
Step 1 takes care of even numbers. And after step 1, all remaining prime factor must be odd (difference of two prime factors must be at least 2), this explains why i is incremented by 2.
Now the main part is, the loop runs till square root of n not till. To prove that this optimization works, let us consider the following property of composite numbers.
Every composite number has at least one prime factor less than or equal to square root of itself.
This property can be proved using counter statement. Let a and b be two factors of n such that a*b = n. If both are greater than √n, then a.b > √n, * √n, which contradicts the expression “a * b = n”.
void primeFactors(int n){ // Print the number of 2s that divide n while (n%2 == 0) { printf("%d ", 2); n = n/2; } // n must be odd at this point. So we can skip one element (Note i = i +2) for (int i = 3; i <= sqrt(n); i = i+2) { // While i divides n, print i and divide n while (n%i == 0) { printf("%d ", i); n = n/i; } } // This condition is to handle the case whien n is a prime number // greater than 2 if (n > 2) printf ("%d ", n);}A composite number is a positive integer that has at least one positive divisor other than one or the number itself. In other words, a composite number is any integer greater than one that is not a prime number.
https://www.quora.com/Which-is-the-fastest-prime-factorization-algorithm-to-date
http://introcs.cs.princeton.edu/java/78crypto/PollardRho.java.html
http://www.acmerblog.com/jiudu-1207-2363.html
九度-1207-质因数的个数[解题代码]
求正整数N(N>1)的质因数的个数。
相同的质因数需要重复计算。如120=2*2*2*3*5,共有5个质因数。
06 | public static void main(String[] args) { |
07 | Scanner s = new Scanner(new BufferedInputStream(System.in)); |
08 | while(s.hasNextLong()){ |
09 | n = s.nextLong(); |
10 | int m = (int) Math.sqrt(n); |
11 | int count = 0; |
12 | while(n>1){ |
13 | int i; |
14 | for(i=2; i<=m; i++){ |
15 | if(n%i == 0){ |
16 | count ++; |
17 | n /= i; |
18 | break; |
19 | } |
20 | } |
21 | if(i == m+1 && n>1){ |
22 | count ++; |
23 | break; |
24 | } |
25 | } |
26 | System.out.println(count); |
27 | |
28 | } |
29 | } |