Analysis of Algorithms Time Complexity

https://math.stackexchange.com/questions/1865688/what-is-the-computational-complexity-of-newton-raphson-method-to-find-square-roo

The average theoretical complexity is 𝑙𝑜𝑔2(𝑁)$lo{g}_2(N)$. However, two notes:

𝑙𝑜𝑔2(𝑁)$lo{g}_2(N)$ is just the highest order term. The actual number of steps to convergence might be:

constant term + coefficient*𝑙𝑜𝑔2(𝑁)$lo{g}_2(N)$

Secondly, there can be some nuance about the exact floating point computations, etc. where convergence might occur a step sooner or later, before x and y converge to within "machine epsilon" (i.e. so close that they can't be distinguished).

Basically, don't worry. The number of steps to convergence roughly follows 𝑙𝑜𝑔2(𝑁)$lo{g}_2(N)$. If you did more iterations, it would more perfectly fit 𝑙𝑜𝑔2(𝑁)$lo{g}_2(N)$.

https://www.cs.cornell.edu/courses/cs3110/2012sp/lectures/lec20-master/lec20.html

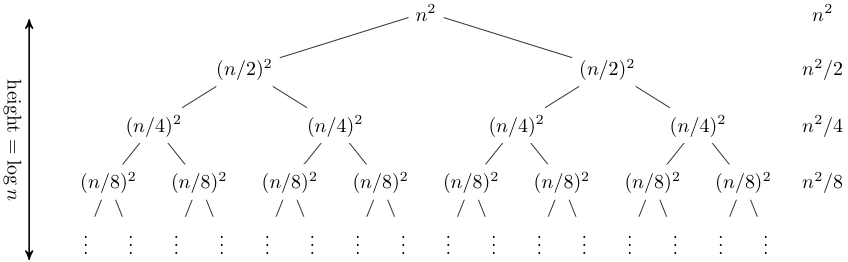
Recursion Trees

A recursion tree is useful for visualizing what happens when a recurrence is iterated. It diagrams the tree of recursive calls and the amount of work done at each call.

For instance, consider the recurrence

T(n) = 2T(n/2) + n².

The recursion tree for this recurrence has the following form:

In this case, it is straightforward to sum across each row of the tree to obtain the total work done at a given level:

This a geometric series, thus in the limit the sum is O(n²). The depth of the tree in this case does not really matter; the amount of work at each level is decreasing so quickly that the total is only a constant factor more than the root.

Recursion trees can be useful for gaining intuition about the closed form of a recurrence, but they are not a proof (and in fact it is easy to get the wrong answer with a recursion tree, as is the case with any method that includes ''...'' kinds of reasoning). As we saw last time, a good way of establishing a closed form for a recurrence is to make an educated guess and then prove by induction that your guess is indeed a solution. Recurrence trees can be a good method of guessing.

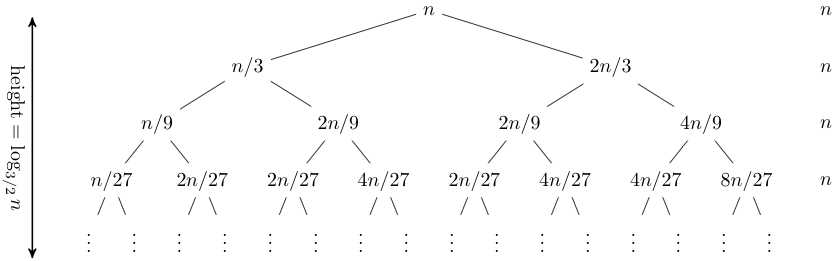
Let's consider another example,

T(n) = T(n/3) + T(2n/3) + n.

Expanding out the first few levels, the recurrence tree is:

Note that the tree here is not balanced: the longest path is the rightmost one, and its length is log_3/2 n. Hence our guess for the closed form of this recurrence is O(n log n).

https://www.geeksforgeeks.org/analysis-algorithm-set-4-master-method-solving-recurrences/

T(n) = aT(n/b) + f(n) where a >= 1 and b > 1

There are following three cases:
1. If f(n) = Θ(nc) where c < Logba then T(n) = Θ(nLogba)

2. If f(n) = Θ(nc) where c = Logba then T(n) = Θ(ncLog n)

3.If f(n) = Θ(nc) where c > Logba then T(n) = Θ(f(n))

How does this work?
Master method is mainly derived from recurrence tree method. If we draw recurrence tree of T(n) = aT(n/b) + f(n), we can see that the work done at root is f(n) and work done at all leaves is Θ(nc) where c is Logba. And the height of recurrence tree is Logbn

In recurrence tree method, we calculate total work done. If the work done at leaves is polynomially more, then leaves are the dominant part, and our result becomes the work done at leaves (Case 1). If work done at leaves and root is asymptotically same, then our result becomes height multiplied by work done at any level (Case 2). If work done at root is asymptotically more, then our result becomes work done at root (Case 3).

http://www.geeksforgeeks.org/interesting-time-complexity-question/

int fun(int n) {        for (int i = 1; i <= n; i++)     {         for (int j = 1; j < n; j += i)         {             // Some O(1) task         }     }    }

For i = 1, the inner loop is executed n times.
For i = 2, the inner loop is executed approximately n/2 times.
For i = 3, the inner loop is executed approximately n/3 times.
For i = 4, the inner loop is executed approximately n/4 times.
…………………………………………………….
…………………………………………………….
For i = n, the inner loop is executed approximately n/n times.

So the total time complexity of the above algorithm is (n + n/2 + n/3 + … + n/n)

Which becomes n * (1/1 + 1/2 + 1/3 + … + 1/n)

The important thing about series (1/1 + 1/2 + 1/3 + … + 1/n) is, it is equal to Θ(Logn) (See this for reference). So the time complexity of the above code is Θ(nLogn).

O(N)
http://geeksquiz.com/algorithms-analysis-of-algorithms-question-3/

What is time complexity of fun()?

int fun(int n) {   int count = 0;   for (int i = n; i > 0; i /= 2)      for (int j = 0; j < i; j++)         count += 1;   return count; } (C) O(n) For a input integer n, the innermost statement of fun() is executed following times. So time complexity T(n) can be written as T(n) = O(n + n/2 + n/4 + … 1) = O(n) The value of count is also n + n/2 + n/4 + .. + 1

http://geeksquiz.com/algorithms-analysis-of-algorithms-question-13/

void fun(int n, int arr[]) {     int i = 0, j = 0;     for(; i < n; ++i)         while(j < n && arr[i] < arr[j])             j++; }

(A) O(n)

But, please note that the variable j is not initialized for each value of variable i. So, the inner loop runs at most n times. 
http://geeksquiz.com/algorithms-analysis-of-algorithms-question-5/

int fun(int n) {   int count = 0;   for (int i = 0; i < n; i++)      for (int j = i; j > 0; j--)         count = count + 1;   return count; }

(B) Theta (n^2)

The time complexity can be calculated by counting number of times the expression “count = count + 1;” is executed. The expression is executed 0 + 1 + 2 + 3 + 4 + …. + (n-1) times.

Time complexity = Theta(0 + 1 + 2 + 3 + .. + n-1) = Theta (n*(n-1)/2) = Theta(n^2)

http://geeksquiz.com/algorithms-analysis-of-algorithms-question-24/

int recursive (mt n) {    if (n == 1)      return (1);    else      return (recursive (n-1) + recursive (n-1)); }

(D) 0(2^n)
Explanation: Recursive expression for the above program will be.

  T(n) = 2T(n-1) + c
  T(1) = c1.

Let us solve it.

  T(n) = 2(2T(n-2) + c) + c        = 4T(n-2) + 3c
  T(n) = 8T(n-3) + 6c + c          =  8T(n-3) + 7c
  T(n) = 16T(n-4) + 14c + c        =  16T(n-4) + 15c
  ............................................................
  .............................................................
  T(n) = (2^(n-1))T(1) +  (2^(n-1) - 1)c

  T(n) = O(2^n)

http://www.geeksforgeeks.org/data-structures-and-algorithms-set-11/

What is the time complexity of the following recursive function:

int DoSomething (int n) {   if (n <= 2)     return 1;   else      return (DoSomething (floor(sqrt(n))) + n); }

(D) Θ(loglogn)

Recursive relation for the DoSomething() is

  T(n) =  T(√n) + C1 if n > 2  

We have ignored the floor() part as it doesn’t matter here if it’s a floor or ceiling.

  Let n = 2^m,  T(n) = T(2^m)
  Let T(2^m) =  S(m)

  From the above two, T(n) = S(m)

  S(m) = S(m/2) + C1  /* This is simply binary search recursion*/
  S(m)  = O(logm)      
          = O(loglogn)  /* Since n = 2^m */
  
  Now, let us go back to the original recursive function T(n) 
  T(n)  = S(m) 
          = O(LogLogn)

4. In the following C function, let n >= m.

http://mathworld.wolfram.com/EuclideanAlgorithm.html

int gcd(n,m) {   if (n%m ==0) return m;    n = n%m;   return gcd(m,n); }

How many recursive calls are made by this function?
(A) Θ(logn)?

Difficult
http://geeksquiz.com/algorithms-analysis-of-algorithms-question-18-3/

 int unknown(int n) {
    int i, j, k = 0;
    for (i  = n/2; i <= n; i++)
        for (j = 2; j <= n; j = j * 2)
            k = k + n/2;
    return k;
 }

The outer loop runs n/2 or

times. The inner loop runs

times (Note that j is divide by 2 in every iteration). So the statement “k = k + n/2;” runs

times. The statement increases value of k by n/2. So the value of k becomes n/2*

which is

http://geeksquiz.com/tag/analysis-of-algorithms-recurrences/
Master Theorem
http://geeksquiz.com/algorithms-analysis-of-algorithms-recurrences-question-11/
Change of variables: let m = lg n. Recurrence becomes S(m) = S(m/2) + theta(lgm). Case 2 of master’s theorem applies, so T(n) = theta( (log Log n) ^ 2).

http://staff.ustc.edu.cn/~csli/graduate/algorithms/book6/chap03.htm
For positive integers n, the nth harmonic number is

Miscs
http://geeksquiz.com/algorithms-analysis-of-algorithms-question-19-2/

T(n) = T(n-1) + C which is O(n)

Time complexity of fun2() can be written as
T(n) = 2T(n-1) + C which is O(2^n)

What does it mean when we say that an algorithm X is asymptotically more efficient than Y?
(B) X will be a better choice for all inputs except small inputs
The worst case time complexity is always greater than or same as the average case time complexity.
(C)  

Consider the following program fragment for reversing the digits in a given integer to obtain a new integer. Let n = D1D2…Dm

int n, rev; rev = 0; while (n > 0) {    rev = rev*10 + n%10;    n = n/10; }

The loop invariant condition at the end of the ith iteration is: (GATE CS 2004)
(A) n = D1D2….Dm-i and rev = DmDm-1…Dm-i+1

We can get it by taking an example like n = 54321. After 2 iterations, rev would be 12 and n would be 543.