Massive Algorithms: Bellman-Ford Algorithm

Bellman-Ford Algorithm

https://www.quora.com/How-is-the-Bellman-Ford-algorithm-a-case-of-dynamic-programming

It's definitely reasonable to think of it that way. After all, we can write a recurrence for the shortest path of length L from the source to vertex V:

F(V, L) = min [over all neighbors N of V] (F(N, L-1) + edge_cost(N, V))

https://www.programiz.com/dsa/bellman-ford-algorithm

Negative weight edges can create negative weight cycles i.e. a cycle which will reduce the total path distance by coming back to the same point.

negative weight cycles can give an incorrect result when trying to find out the shortest path

Shortest path algorithms like Dijkstra's Algorithm that aren't able to detect such a cycle can give an incorrect result because they can go through a negative weight cycle and reduce the path length.

Bellman Ford algorithm works by overestimating the length of the path from the starting vertex to all other vertices. Then it iteratively relaxes those estimates by finding new paths that are shorter than the previously overestimated paths.

By doing this repeatedly for all vertices, we are able to guarantee that the end result is optimized.

Bellman Ford's algorithm and Dijkstra's algorithm are very similar in structure. While Dijkstra looks only to the immediate neighbours of a vertex, Bellman goes through each edge in every iteration.

https://brilliant.org/wiki/bellman-ford-algorithm/

There are a few, short steps to proving Bellman-Ford. The first step shows that each iteration of Bellman-Ford reduces the distance of each vertex in the appropriate way. The second step shows that once the algorithm has terminated, if there are no negative weight cycles, the resulting distances are perfectly correct. The final step shows that if that is not the case, then there is indeed a negative weight cycle, which proves the Bellman-Ford negative cycle detection.

for v in V:
    v.distance = infinity
    v.p = None
source.distance = 0
for i from 1 to |V| - 1:
    for (u, v) in E:
        relax(u, v)
for (u, v) in E:
    if v.distance > u.distance + weight(u, v):
        print "A negative weight cycle exists"

https://blog.csdn.net/u012413167/article/details/50932949

假设s到v的最短真实距离是v.r

有如下引理：

假入s->vk的最短路径为p=<v0,v1,v2,...vk>,并且我们队p中的边所进行的松弛顺序为（v0,v1)，（v1，v2），...，（Vk-1,Vk),则vk.d=v.r。该性质的成立与其他任何松弛操作无关，即使这些松弛操作是与对p上的边所进行的松弛操作穿插进行的。

有了以上引理，第i轮循环就可以看做是对(vi-1,vi)进行松弛。所以经过｜Ｖ｜－１轮后，对于所有v∈V,都有v.d=v.r

所以可以得到s到所有顶点的最短距离

https://www.cnblogs.com/willaty/p/8243881.html

求最短路证明：

一。假设某点与源点不连通。

由于初始化时，除了源点距离初始为0之外，其他点都初始化为无穷大，如果不连通，则某点所在的连通图的任一条边都不会导致更新。

二。假设x点与源点连通。

每个点都存在自己的最短路，为（e0, e1, e2, ..., ek）。

显然，源点只要经过n - 1条边就可到达任一点；　　（一）

现只需证明，对x点，每次迭代（松弛），至少有一条最短边ei的距离被找到，除非已经到达x点。　　（二）

　　对于第一次迭代，必定更新和源点相连的所有边（如果是有向图，则是指出去的），由于源点距离是0，和其相连的都是无穷大。

　　　　而这些往外连的边中，必有一条是x点的最短路上起始的一条边。

　　则设有点k，这个点是x最短路上的一个点，下一次松弛，必能找到下一个点，且也是x的最短路上的一个点：

　　　　由于下一次松弛将更新与k相连的所有点。

有（一）（二）可得，上面两次迭代可以找出最短路。

而关于负权环的判断：

由于负权环的存在，可以通过不断绕着走从而减小环上各个点的距离。

所以即使迭代完成，当判断是否还能更新时，会发现还是可以更新的，这就判断了存在负权环。
https://github.com/williamfiset/Algorithms/blob/master/com/williamfiset/algorithms/graphtheory/BellmanFordEdgeList.java

  public static double[] bellmanFord(Edge[] edges, int V, int start) {

    double[] dist = new double[V];
    java.util.Arrays.fill(dist, Double.POSITIVE_INFINITY);
    dist[start] = 0;

    // Only in the worst case does it take V-1 iterations for the Bellman-Ford
    // algorithm to complete. Another stopping condition is when we're unable to
    // relax an edge, this means we have reached the optimal solution early.
    boolean relaxedAnEdge = true;

    // For each vertex, apply relaxation for all the edges
    for (int v = 0; v < V-1 && relaxedAnEdge; v++) {
      relaxedAnEdge = false;
      for (Edge edge : edges) {
        if (dist[edge.from] + edge.cost < dist[edge.to]) {
          dist[edge.to] = dist[edge.from] + edge.cost;
          relaxedAnEdge = true;
        }
      }
    }

    // Run algorithm a second time to detect which nodes are part
    // of a negative cycle. A negative cycle has occurred if we 
    // can find a better path beyond the optimal solution.
    relaxedAnEdge = true;
    for (int v = 0; v < V-1 && relaxedAnEdge; v++) {
      relaxedAnEdge = false;
      for (Edge edge : edges) {
        if (dist[edge.from] + edge.cost < dist[edge.to]) {
          dist[edge.to] = Double.NEGATIVE_INFINITY;
          relaxedAnEdge = true;
        }
      }
    }

    // Return the array containing the shortest distance to every node
    return dist;

  }

https://www.geeksforgeeks.org/bellman-ford-algorithm-dp-23/

Given a graph and a source vertex src in graph, find shortest paths from src to all vertices in the given graph. The graph may contain negative weight edges.
We have discussed Dijkstra’s algorithm for this problem. Dijksra’s algorithm is a Greedy algorithm and time complexity is O(VLogV) (with the use of Fibonacci heap). Dijkstra doesn’t work for Graphs with negative weight edges, Bellman-Ford works for such graphs. Bellman-Ford is also simpler than Dijkstra and suites well for distributed systems. But time complexity of Bellman-Ford is O(VE), which is more than Dijkstra.

Algorithm:O(VE)

Output: Shortest distance to all vertices from src. If there is a negative weight cycle, then shortest distances are not calculated, negative weight cycle is reported.

1) This step initializes distances from source to all vertices as infinite and distance to source itself as 0. Create an array dist[] of size |V| with all values as infinite except dist[src] where src is source vertex.

2) This step calculates shortest distances. Do following |V|-1 times where |V| is the number of vertices in given graph.
…..a) Do following for each edge u-v
………………If dist[v] > dist[u] + weight of edge uv, then update dist[v]
………………….dist[v] = dist[u] + weight of edge uv

3) This step reports if there is a negative weight cycle in graph. Do following for each edge u-v
……If dist[v] > dist[u] + weight of edge uv, then “Graph contains negative weight cycle”
The idea of step 3 is, step 2 guarantees shortest distances if graph doesn’t contain negative weight cycle. If we iterate through all edges one more time and get a shorter path for any vertex, then there is a negative weight cycle

How does this work? Like other Dynamic Programming Problems, the algorithm calculate shortest paths in bottom-up manner. It first calculates the shortest distances for the shortest paths which have at-most one edge in the path. Then, it calculates shortest paths with at-nost 2 edges, and so on. After the ith iteration of outer loop, the shortest paths with at most i edges are calculated. There can be maximum |V| – 1 edges in any simple path, that is why the outer loop runs |v| – 1 times. The idea is, assuming that there is no negative weight cycle, if we have calculated shortest paths with at most i edges, then an iteration over all edges guarantees to give shortest path with at-most (i+1) edges (Proof is simple, you can refer this or MIT Video Lecture)

2) Bellman-Ford works better (better than Dijksra’s) for distributed systems. Unlike Dijksra’s where we need to find minimum value of all vertices, in Bellman-Ford, edges are considered one by one.
Graph presentation: just stores a lists of edges(not commonly used adjacent matrix or list)

    void BellmanFord(Graph graph,int src) 

    { 

        int V = graph.V, E = graph.E; 

        int dist[] = new int[V]; 

        // Step 1: Initialize distances from src to all other 

        // vertices as INFINITE 

        for (int i=0; i<V; ++i) 

            dist[i] = Integer.MAX_VALUE; 

        dist[src] = 0; 

        // Step 2: Relax all edges |V| - 1 times. A simple 

        // shortest path from src to any other vertex can 

        // have at-most |V| - 1 edges 

        for (int i=1; i<V; ++i) 

        { 

            for (int j=0; j<E; ++j) 

            { 

                int u = graph.edge[j].src; 

                int v = graph.edge[j].dest; 

                int weight = graph.edge[j].weight; 

                if (dist[u]!=Integer.MAX_VALUE && 

                    dist[u]+weight<dist[v]) 

                    dist[v]=dist[u]+weight; 

            } 

        } 

        // Step 3: check for negative-weight cycles.  The above 

        // step guarantees shortest distances if graph doesn't 

        // contain negative weight cycle. If we get a shorter 

        //  path, then there is a cycle. 

        for (int j=0; j<E; ++j) 

        { 

            int u = graph.edge[j].src; 

            int v = graph.edge[j].dest; 

            int weight = graph.edge[j].weight; 

            if (dist[u] != Integer.MAX_VALUE && 

                dist[u]+weight < dist[v]) 

              System.out.println("Graph contains negative weight cycle"); 

        } 

        printArr(dist, V); 

    }

Visualization
http://www.comp.nus.edu.sg/~stevenha/visualization/sssp.html
http://en.wikipedia.org/wiki/Bellman%E2%80%93Ford_algorithm
The Bellman–Ford algorithm is slower than Dijkstra's algorithm for the same problem, but more versatile, as it is capable of handling graphs in which some of the edge weights are negative numbers.

Like Dijkstra's Algorithm, Bellman–Ford is based on the principle ofrelaxation, in which an approximation to the correct distance is gradually replaced by more accurate values until eventually reaching the optimum solution.

However, Dijkstra's algorithm greedilyselects the minimum-weight node that has not yet been processed, and performs this relaxation process on all of its outgoing edges; by contrast, the Bellman–Ford algorithm simply relaxes all the edges, and does this

|V|-1

times, where

|V|

is the number of vertices in the graph. In each of these repetitions, the number of vertices with correctly calculated distances grows, from which it follows that eventually all vertices will have their correct distances. This method allows the Bellman–Ford algorithm to be applied to a wider class of inputs than Dijkstra.

Bellman–Ford runs in

O(|V|\cdot |E|)

time, where

|V|

and

|E|

are the number of vertices and edges respectively.

Simply put, the algorithm initializes the distance to the source to 0 and all other nodes to infinity. Then for all edges, if the distance to the destination can be shorten by taking the edge, the distance is updated to the new lower value. At each iteration

i

that the edges are scanned, the algorithm finds all shortest paths of at most length

i

edges. Since the longest possible path without a cycle can be

|V|-1

edges, the edges must be scanned

|V|-1

times to ensure the shortest path has been found for all nodes.

function BellmanFord(list vertices, list edges, vertex source)
   ::weight[],predecessor[]
   // Step 1: initialize graph
   for each vertex v in vertices:
       if v is source then weight[v] := 0
       else weight[v] := infinity
       predecessor[v] := null

   // Step 2: relax edges repeatedly
   for i from 1 to size(vertices)-1:
       for each edge (u, v) with weight w in edges:
           if weight[u] + w < weight[v]:
               weight[v] := weight[u] + w
               predecessor[v] := u

   // Step 3: check for negative-weight cycles
   for each edge (u, v) with weight w in edges:
       if weight[u] + w < weight[v]:
           error "Graph contains a negative-weight cycle"
   return weight[], predecessor[]

Proof of correctness

The correctness of the algorithm can be shown by induction. The precise statement shown by induction is:

Lemma. After i repetitions of for cycle:

If Distance(u) is not infinity, it is equal to the length of some path from s to u;
If there is a path from s to u with at most i edges, then Distance(u) is at most the length of the shortest path from s to u with at most i edges.

Relaxing an edge means checking to see if the path to the node the edge is pointing to can’t be shortened, and if so, doing it.
http://java.dzone.com/articles/algorithm-week-bellman-ford

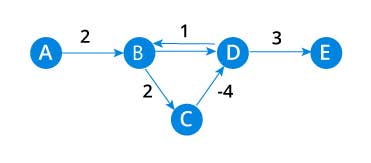
In this very basic image we can see how Bellman-Ford solves the problem. First we get the distances from S to A and B, which are respectively 3 and 4, but there is a shorter path to A, which passes through B and it is (S, B) + (B, A) = 4 – 2 = 2.

Java Implementation

https://gist.github.com/nodirt/4b780f5d0bc4e0fe1b8b
public static int BellmanFord(WeightableDiGraph g){
Arrays.fill(dist, Long.MAX_VALUE);
Arrays.fill(prev, -1);
dist[0] = 0;
for(int i = 1; i < g.V() - 1; i++){
for(DirectedEdge e : g.adj(i)){

if(dist[e.to()] > dist[e.from()] + e.weight()){
dist[e.to()] = dist[e.from()] + e.weight();
prev[e.to()] = e.to();
}
}
}

for(int i = 0; i < g.V(); i++){
for(DirectedEdge e : g.adj(i)){
if(dist[e.to()] > dist[e.from()] + e.weight())
return 1;
}
}
return 0;
}
http://learn.yancyparedes.net/2013/10/an-implementation-of-bellman-fords-algorithm/

    public static void main(String[] args) throws FileNotFoundException {

        Scanner iFile = new Scanner(new FileReader("ShortestPaths.txt"));

        int K = iFile.nextInt();

        for(int c = 1; c <= K; c++) {

            int N = iFile.nextInt();

            int M = iFile.nextInt();

            int[] d = new int[N];

            Edge[] edges = new Edge[M];

            System.out.printf("Case #%d:\n", c);

            // initialization

            for(int i = 1; i < N; i++)

                d[i] = Integer.MAX_VALUE;

            // read all edges

            for(int i = 0; i < M; i++)

                edges[i] = new Edge(iFile.nextInt(), iFile.nextInt(), iFile.nextInt());

            // relaxation

            for(int i = 0; i < N-1; i++) {

                for(int j = 0; j < M; j++) {

                    Edge e = edges[j];

                    if(d[e.d] > d[e.s] + e.w)

                        d[e.d] = d[e.s] + e.w;

}

}

            boolean flag = false;

            // reporting

            for(int j = 0; j < M; j++) {

                Edge e = edges[j];

                if(d[e.d] > d[e.s] + e.w) {

                    System.out.println("  No solution -- graph has a negative cycle.");

                    flag = true;

}

}

            for(int i = 0; !flag && i < N; i++)

                System.out.printf("  %d --> %d : %d\n", 0, i, d[i]);

            System.out.println();

}

        iFile.close();

}

http://www.geekviewpoint.com/java/graph/bellman_ford_shortest_path
https://sites.google.com/site/indy256/algo/bellman_ford
O(V^3) if use matrix, O(VE) if uses adjacent list.

public class BellmanFord {

  public Integer[][] singleSourceShortestPath(Integer[][] weight,

          int source) throws Exception

  {

    //auxiliary constants

    final int SIZE = weight.length;

    final int EVE = -1;//to indicate no predecessor

    final int INFINITY = Integer.MAX_VALUE;

    //declare and initialize pred to EVE and minDist to INFINITY

    Integer[] pred = new Integer[SIZE];

    Integer[] minDist = new Integer[SIZE];

    Arrays.fill(pred, EVE);

    Arrays.fill(minDist, INFINITY);

    //set minDist[source] = 0 because source is 0 distance from itself.

    minDist[source] = 0;

    //relax the edge set V-1 times to find all shortest paths

    for (int i = 1; i < minDist.length - 1; i++) { // i==> stpeps

      for (int v = 0; v < SIZE; v++) { // these 2 loops are to iterate all edges

        for (int x : adjacency(weight, v)) {

          if (minDist[x] > minDist[v] + weight[v][x]) {

            minDist[x] = minDist[v] + weight[v][x];

            pred[x] = v;

          }

        }

      }

    }

    //detect cycles if any

    for (int v = 0; v < SIZE; v++) {

      for (int x : adjacency(weight, v)) {

        if (minDist[x] > minDist[v] + weight[v][x]) {

          throw new Exception("Negative cycle found");

        }

      }

    }

    Integer[][] result = {pred, minDist};

    return result;

  }

  private List<Integer> adjacency(Integer[][] G, int v) {

    List<Integer> result = new ArrayList<Integer>();

    for (int x = 0; x < G.length; x++) {

      if (G[v][x] != null) {

        result.add(x);

      }

    }

    return result;

  }

}

http://www.keithschwarz.com/interesting/code/bellman-ford/BellmanFord.java.html

public static <T> Map<T, Double> shortestPaths(DirectedGraph<T> graph, T source) {
        /* Construct a map from the nodes to their distances, then populate it
         * with the initial value of the recurrence (the source is at distance
         * zero from itself; all other nodes are at infinite distance).
         */
        Map<T, Double> result = new HashMap<T, Double>();
        for (T node: graph)
            result.put(node, Double.POSITIVE_INFINITY);
        result.put(source, 0.0);
        /* Create a new map that acts as scratch space.  We'll flip back and
         * forth between the result map and this map during each iteration of
         * the algortihm so that we avoid needlessly reallocating maps.
         */
        Map<T, Double> scratch = new HashMap<T, Double>();
        /* Starting with k = 1, compute the new values for the distances by
         * evaluating the recurrence.
         */
        for (int k = 1; k <= graph.size(); ++k) {
            /* Begin by guessing that each node in this new iteration will have
             * a cost equal to its cost on the previous iteration.
             */
            scratch.putAll(result);
            /* Scan across all the edges in the graph, updating the costs of
             * the paths of the nodes at their endpoints.
             */
            for (T node: graph) {
                for (Map.Entry<T, Double> edge: graph.edgesFrom(node).entrySet()) {
                    /* The new cost of the shortest path to this node is no
                     * greater than the cost of the shortest path to the nodes'
                     * neighbor plus the cost of the edge from that neighbor
                     * into this node.
                     */
                    scratch.put(edge.getKey(), // The node being updated                                Math.min(scratch.get(edge.getKey()),
                                         edge.getValue() + result.get(node)));
                }
            }
            /* Finally, exchange the scratch buffer holding the new result with
             * the result map holding last iteration's results.
             */
            Map<T, Double> temp = result;
            result = scratch;
            scratch = temp;
        }
        /* Finally, report the distances. */
        return result;
    }
http://www.cppblog.com/menjitianya/archive/2015/11/19/212292.html

Bellman-Ford同样也是利用了最短路的最优子结构性质，用d[i]表示起点s到i的最短路，那么边数上限为 j 的最短路可以通过边数上限为 j-1 的最短路加入一条边得到，通过n-1次迭代，最后求得s到所有点的最短路。

具体算法描述如下：对于图G = <V, E>，源点为s，d[i]表示s到i的最短路。

1) 初始化所有顶点 d[i] = INF, 令d[s] = 0，计数器 j = 0；

2) 枚举每条边(u, v)，如果d[u]不等于INF并且 d[u] + w(u, v) < d[v]，则令d[v] = d[u] + w(u, v)；

3) 计数器j + +，当j = n - 1时算法结束，否则继续重复2)的步骤；

第2)步的一次更新称为边的“松弛”操作。

以上算法并没有考虑到负权圈的问题，如果存在负圈权，那么第2)步操作的更新会永无止境，所以判定负权圈的算法也就出来了，只需要在第n次继续进行第2)步的松弛操作，如果有至少一条边能够被更新，那么必定存在负权圈。

TODO:
http://algs4.cs.princeton.edu/44sp/BellmanFordSP.java.html
https://sites.google.com/site/indy256/algo/bellman_ford
Read full article from Dynamic Programming | Set 23 (Bellman–Ford Algorithm) - GeeksforGeeks

Bellman-Ford Algorithm

Labels

Popular Posts