Given n line segments, find if any two segments intersect

https://www.geeksforgeeks.org/given-a-set-of-line-segments-find-if-any-two-segments-intersect/

We have discussed the problem to detect if two given line segments intersect or not. In this post, we extend the problem. Here we are given n line segments and we need to find out if any two line segments intersect or not.

Naive Algorithm A naive solution to solve this problem is to check every pair of lines and check if the pair intersects or not. We can check two line segments in O(1) time. Therefore, this approach takes O(n2).

Sweep Line Algorithm: We can solve this problem in O(nLogn) time using Sweep Line Algorithm. The algorithm first sorts the end points along the x axis from left to right, then it passes a vertical line through all points from left to right and checks for intersections. Following are detailed steps.

1) Let there be n given lines. There must be 2n end points to represent the n lines. Sort all points according to x coordinates. While sorting maintain a flag to indicate whether this point is left point of its line or right point.

2) Start from the leftmost point. Do following for every point
…..a) If the current point is a left point of its line segment, check for intersection of its line segment with the segments just above and below it. And add its line to active line segments (line segments for which left end point is seen, but right end point is not seen yet).  Note that we consider only those neighbors which are still active.
….b) If the current point is a right point, remove its line segment from active list and check whether its two active neighbors (points just above and below) intersect with each other.

The step 2 is like passing a vertical line from all points starting from the leftmost point to the rightmost point. That is why this algorithm is called Sweep Line Algorithm. The Sweep Line technique is useful in many other geometric algorithms like calculating the 2D Voronoi diagram

What data structures should be used for efficient implementation?
In step 2, we need to store all active line segments. We need to do following operations efficiently:
a) Insert a new line segment
b) Delete a line segment
c) Find predecessor and successor according to y coordinate values
The obvious choice for above operations is Self-Balancing Binary Search Tree like AVL Tree, Red Black Tree. With a Self-Balancing BST, we can do all of the above operations in O(Logn) time.
Also, in step 1, instead of sorting, we can use min heap data structure. Building a min heap takes O(n) time and every extract min operation takes O(Logn) time (See this).

sweepLineIntersection(Points[0..2n-1]):
1. Sort Points[] from left to right (according to x coordinate)

2. Create an empty Self-Balancing BST T. It will contain all active line 
   Segments ordered by y coordinate.

// Process all 2n points 
3. for i = 0 to 2n-1

    // If this point is left end of its line  
    if (Points[i].isLeft) 
       T.insert(Points[i].line())  // Insert into the tree

       // Check if this points intersects with its predecessor and successor
       if ( doIntersect(Points[i].line(), T.pred(Points[i].line()) )
         return true
       if ( doIntersect(Points[i].line(), T.succ(Points[i].line()) )
         return true

    else  // If it's a right end of its line
       // Check if its predecessor and successor intersect with each other
       if ( doIntersect(T.pred(Points[i].line(), T.succ(Points[i].line()))
         return true
       T.delete(Points[i].line())  // Delete from tree

4. return False

https://algorithmtutor.com/Computational-Geometry/Check-if-any-two-line-segments-intersect-given-n-line-segments/

def compare(p1, p2): if p1.x < p2.x: return -1 elif p1.x > p2.x: return 1 if p1.x == p2.x: if p1.ptype == p2.ptype: if p1.y < p2.y: return -1 else: return 1 else: if p1.ptype == 0: return -1 else: return 1 def any_segments_intersect(S): # Step 1 T = RedBlackTree() # Step 2 sortedS = sorted(S, cmp=lambda x,y: compare(x,y)) sortedS = map(lambda x: Node(x), sortedS) # Step 3 for point in sortedS: if point.key.ptype == 0: T.insert(point) prd = T.predecessor(point) if prd and intersect(point.key, point.key.other_end, prd.key, prd.key.other_end): return True ssc = T.successor(point) if ssc and intersect(point.key, point.key.other_end, ssc.key, ssc.key.other_end): return True if point.key.ptype == 1: prd = T.predecessor(point) ssc = T.successor(point) if prd and ssc: if intersect(prd.key, prd.key.other_end, ssc.key, ssc.key.other_end): return True T.delete(point) return False

https://www.geeksforgeeks.org/check-if-two-given-line-segments-intersect/

How to check if two given line segments intersect?

Given two line segments (p1, q1) and (p2, q2), find if the given line segments intersect with each other.

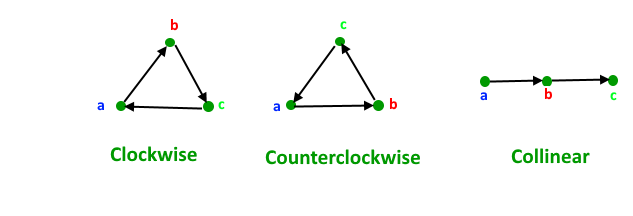
Before we discuss solution, let us define notion of orientation. Orientation of an ordered triplet of points in the plane can be
–counterclockwise
–clockwise
–colinear
The following diagram shows different possible orientations of (a, b, c)

How is Orientation useful here?
Two segments (p1,q1) and (p2,q2) intersect if and only if one of the following two conditions is verified

1. General Case:
– (p1, q1, p2) and (p1, q1, q2) have different orientations and
– (p2, q2, p1) and (p2, q2, q1) have different orientations.

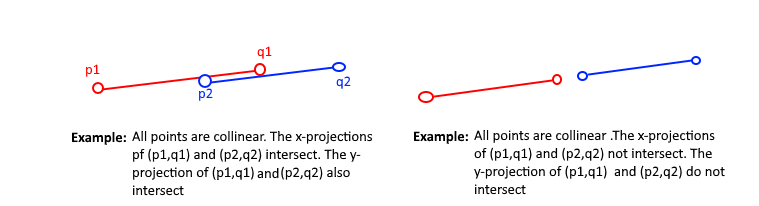
Examples:

2. Special Case
– (p1, q1, p2), (p1, q1, q2), (p2, q2, p1), and (p2, q2, q1) are all collinear and
– the x-projections of (p1, q1) and (p2, q2) intersect
– the y-projections of (p1, q1) and (p2, q2) intersect

Examples:

// Given three colinear points p, q, r, the function checks if

// point q lies on line segment 'pr'

bool onSegment(Point p, Point q, Point r)

{

    if (q.x <= max(p.x, r.x) && q.x >= min(p.x, r.x) &&

        q.y <= max(p.y, r.y) && q.y >= min(p.y, r.y))

       return true;

  

    return false;

}

  

// To find orientation of ordered triplet (p, q, r).

// The function returns following values

// 0 --> p, q and r are colinear

// 1 --> Clockwise

// 2 --> Counterclockwise

int orientation(Point p, Point q, Point r)

{

    // See https://www.geeksforgeeks.org/orientation-3-ordered-points/

    // for details of below formula.

    int val = (q.y - p.y) * (r.x - q.x) -

              (q.x - p.x) * (r.y - q.y);

  

    if (val == 0) return 0;  // colinear

  

    return (val > 0)? 1: 2; // clock or counterclock wise

}

  

// The main function that returns true if line segment 'p1q1'

// and 'p2q2' intersect.

bool doIntersect(Point p1, Point q1, Point p2, Point q2)

{

    // Find the four orientations needed for general and

    // special cases

    int o1 = orientation(p1, q1, p2);

    int o2 = orientation(p1, q1, q2);

    int o3 = orientation(p2, q2, p1);

    int o4 = orientation(p2, q2, q1);

  

    // General case

    if (o1 != o2 && o3 != o4)

        return true;

  

    // Special Cases

    // p1, q1 and p2 are colinear and p2 lies on segment p1q1

    if (o1 == 0 && onSegment(p1, p2, q1)) return true;

  

    // p1, q1 and q2 are colinear and q2 lies on segment p1q1

    if (o2 == 0 && onSegment(p1, q2, q1)) return true;

  

    // p2, q2 and p1 are colinear and p1 lies on segment p2q2

    if (o3 == 0 && onSegment(p2, p1, q2)) return true;

  

     // p2, q2 and q1 are colinear and q1 lies on segment p2q2

    if (o4 == 0 && onSegment(p2, q1, q2)) return true;

  

    return false; // Doesn't fall in any of the above cases

}

Read full article from Given n line segments, find if any two segments intersect - GeeksforGeeks