http://buttercola.blogspot.com/2015/08/leetcode-skyline-problem.html


X. Use TreeMap instead of PQ
https://blog.csdn.net/gqk289/article/details/56848203
https://blog.csdn.net/magicbean2/article/details/73613204
这道题目算是Leetcode里面比较难的一道了,估计在实际面试中很难遇到。不过由于这算一道典型的扫描线算法(sweep line)类型的题目,所以我在这里好好总结一下网上一个非常好的算法及其代码:
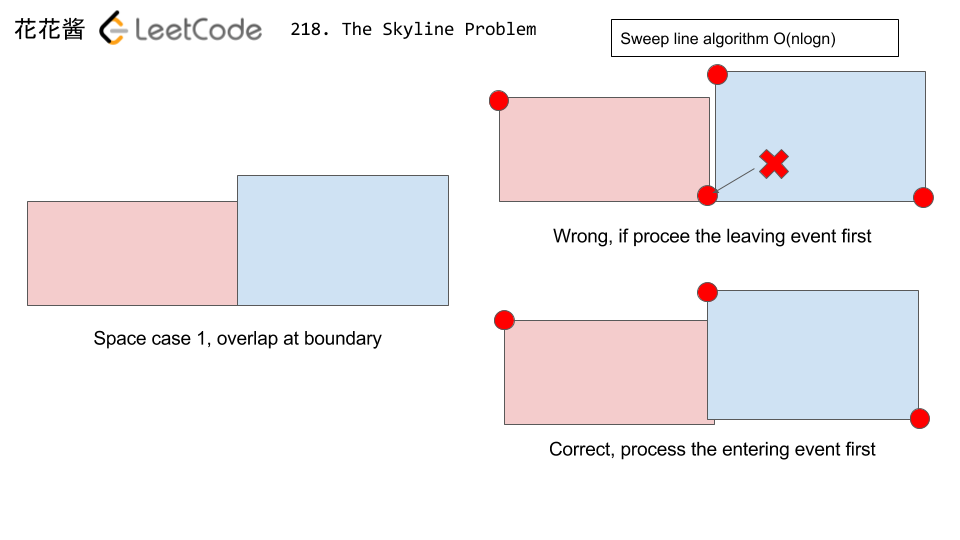
1)将起点连同高度与终点连同高度各作为一个pair都统一保存到一个数组中,然后进行排序。为区分起点和终点,将起点高度设为负值,这样的好处是如果有另外一个终点和起点的x坐标一样,排序之后起点会在前面,也就是在同一个x坐标处,我们会优先处理起点。
2)采用扫描线算法依次处理我们前面排好序的数组中的元素。如果是起点,就将其高度放到multiset中;如果是终点,就在multiset中将其起点删除掉。接着还需要检查删除前后multiset中的最大值是否发生改变,如果发生改变了,则说明这个点就是边际点,将其加入结果集中。
一个实现中特别容易犯的错误就是在multiset中按值删除,这样会将所有等于这个值的点都删除。正确的做法是采用find方法找到等于该值的第一个指针,然后删除该指针,这样可以保证只删除一个。实现中的另外一个小技巧是首先在multiset中添加一个0值,这样可以保证将第一个高度不为0的建筑的起点加入结果集中。
http://www.cnblogs.com/grandyang/p/4534586.html
要是非要在之前的题目中找一道类似的题,也就只有 Merge Intervals 合并区间了吧,但是与那题不同的是,这道题不是求被合并成的空间,而是求轮廓线的一些关键的转折点,这就比较复杂了,我们通过仔细观察题目中给的那个例子可以发现,要求的红点都跟每个小区间的左右区间点有密切的关系,而且进一步发现除了每一个封闭区间的最右边的结束点是楼的右边界点,其余的都是左边界点,而且每个红点的纵坐标都是当前重合处的最高楼的高度,但是在右边界的那个楼的就不算了。在网上搜了很多帖子,发现网友Brian Gordon的帖子图文并茂,什么动画渐变啊,横向扫描啊,简直叼到没朋友啊,但是叼到极致后就懒的一句一句的去读了,这里博主还是讲解另一位网友百草园的博客吧。这里用到了multiset数据结构,其好处在于其中的元素是按堆排好序的,插入新元素进去还是有序的,而且执行删除元素也可方便的将元素删掉。这里为了区分左右边界,将左边界的高度存为负数,建立左边界和负高度的pair,再建立右边界和高度的pair,存入数组中,都存进去了以后,给数组按照左边界排序,这样我们就可以按顺序来处理那些关键的节点了。我们要在multiset中放入一个0,这样在某个没有和其他建筑重叠的右边界上,我们就可以将封闭点存入结果res中。下面我们按顺序遍历这些关键节点,如果遇到高度为负值的pair,说明是左边界,那么将正高度加入multiset中,然后取出此时集合中最高的高度,即最后一个数字,然后看是否跟pre相同,这里的pre是上一个状态的高度,初始化为0,所以第一个左边界的高度绝对不为0,所以肯定会存入结果res中。接下来如果碰到了一个更高的楼的左边界的话,新高度存入multiset的话会排在最后面,那么此时cur取来也跟pre不同,可以将新的左边界点加入结果res。第三个点遇到绿色建筑的左边界点时,由于其高度低于红色的楼,所以cur取出来还是红色楼的高度,跟pre相同,直接跳过。下面遇到红色楼的右边界,此时我们首先将红色楼的高度从multiset中删除,那么此时cur取出的绿色楼的高度就是最高啦,跟pre不同,则可以将红楼的右边界横坐标和绿楼的高度组成pair加到结果res中,这样就成功的找到我们需要的拐点啦,后面都是这样类似的情况。当某个右边界点没有跟任何楼重叠的话,删掉当前的高度,那么multiset中就只剩0了,所以跟当前的右边界横坐标组成pair就是封闭点啦
http://www.cnblogs.com/easonliu/p/4531020.html
https://briangordon.github.io/2014/08/the-skyline-problem.html
However, there is a small thing that can be improved. pq.remove() is O(n) hence make it slower. I have modified it a little bit to use TreeMap instead of PriorityQueue and the run time is 2.5X faster.
The basic idea of this solutions is to find the critical points that change the max height among the buildings on the left
https://discuss.leetcode.com/topic/38065/java-solution-using-priority-queue-and-sweepline
https://discuss.leetcode.com/topic/26890/a-java-solution-by-iteratively-checking-the-starting-and-ending-points
https://discuss.leetcode.com/topic/28482/once-for-all-explanation-with-clean-java-code-o-n-2-time-o-n-space
https://discuss.leetcode.com/topic/22482/short-java-solution
根据position从前到后扫描每一个edge,将edge根据是入还是出来将当前height加入或者移除heap。再得到当前最高点来决定是否加入最终结果。
X. Divide and conquer
https://discuss.leetcode.com/topic/16511/share-my-divide-and-conquer-java-solution-464-ms
http://www.geeksforgeeks.org/divide-and-conquer-set-7-the-skyline-problem/
A city's skyline is the outer contour of the silhouette formed by all the buildings in that city when viewed from a distance. Now suppose you are given the locations and height of all the buildings as shown on a cityscape photo (Figure A), write a program to output the skyline formed by these buildings collectively (Figure B).


The geometric information of each building is represented by a triplet of integers
[Li, Ri, Hi], where Li and Ri are the x coordinates of the left and right edge of the ith building, respectively, and Hi is its height. It is guaranteed that 0 ≤ Li, Ri ≤ INT_MAX, 0 < Hi ≤ INT_MAX, and Ri - Li > 0. You may assume all buildings are perfect rectangles grounded on an absolutely flat surface at height 0.
For instance, the dimensions of all buildings in Figure A are recorded as:
[ [2 9 10], [3 7 15], [5 12 12], [15 20 10], [19 24 8] ] .
The output is a list of "key points" (red dots in Figure B) in the format of
[ [x1,y1], [x2, y2], [x3, y3], ... ] that uniquely defines a skyline. A key point is the left endpoint of a horizontal line segment. Note that the last key point, where the rightmost building ends, is merely used to mark the termination of the skyline, and always has zero height. Also, the ground in between any two adjacent buildings should be considered part of the skyline contour.
For instance, the skyline in Figure B should be represented as:
[ [2 10], [3 15], [7 12], [12 0], [15 10], [20 8], [24, 0] ].
Notes:
- The number of buildings in any input list is guaranteed to be in the range
[0, 10000]. - The input list is already sorted in ascending order by the left x position
Li. - The output list must be sorted by the x position.
- There must be no consecutive horizontal lines of equal height in the output skyline. For instance,
[...[2 3], [4 5], [7 5], [11 5], [12 7]...]is not acceptable; the three lines of height 5 should be merged into one in the final output as such:[...[2 3], [4 5], [12 7], ...]
X. Use TreeMap instead of PQ
https://blog.csdn.net/gqk289/article/details/56848203
将每个建筑左上和右上两个顶点抽出来排序,高度为负的是左顶点为正的是右顶点,然后过一遍treemap,遇到左顶点加入,遇到右顶点移除,如果当前高度与前一高度不同,那么当前顶点及treemap的当前最大高度即为所求一点
public List<int[]> getSkyline(int[][] buildings) {
List<int[]> res = new LinkedList();
List<int[]> height = new LinkedList();
for (int[] building : buildings) {
height.add(new int[] { building[0], -building[2] });
height.add(new int[] { building[1], building[2] });
}
Collections.sort(height, new Comparator<int[]>() {
public int compare(int[] i1, int[] i2) {
if (i1[0] == i2[0]) {
return i1[1] - i2[1];
} else {
return i1[0] - i2[0];
}
}
});
int prev = 0;
TreeMap<Integer, Integer> map = new TreeMap<>(new Comparator<Integer>() {
public int compare(Integer i1, Integer i2) {
return i2 - i1;
}
});
map.put(0, 1);
for (int[] h : height) {
if (h[1] < 0) {
map.put(-h[1], map.getOrDefault(-h[1], 0) + 1);
} else {
Integer cnt = map.get(h[1]);
if (cnt == 1) {
map.remove(h[1]);
} else {
map.put(h[1], map.get(h[1]) - 1);
}
}
int cur = map.firstKey();
if (cur != prev) {
res.add(new int[] { h[0], cur });
prev = cur;
}
}
return res;
}
https://zxi.mytechroad.com/blog/tree/leetcode-218-the-skyline-problem/https://blog.csdn.net/magicbean2/article/details/73613204
这道题目算是Leetcode里面比较难的一道了,估计在实际面试中很难遇到。不过由于这算一道典型的扫描线算法(sweep line)类型的题目,所以我在这里好好总结一下网上一个非常好的算法及其代码:
1)将起点连同高度与终点连同高度各作为一个pair都统一保存到一个数组中,然后进行排序。为区分起点和终点,将起点高度设为负值,这样的好处是如果有另外一个终点和起点的x坐标一样,排序之后起点会在前面,也就是在同一个x坐标处,我们会优先处理起点。
2)采用扫描线算法依次处理我们前面排好序的数组中的元素。如果是起点,就将其高度放到multiset中;如果是终点,就在multiset中将其起点删除掉。接着还需要检查删除前后multiset中的最大值是否发生改变,如果发生改变了,则说明这个点就是边际点,将其加入结果集中。
一个实现中特别容易犯的错误就是在multiset中按值删除,这样会将所有等于这个值的点都删除。正确的做法是采用find方法找到等于该值的第一个指针,然后删除该指针,这样可以保证只删除一个。实现中的另外一个小技巧是首先在multiset中添加一个0值,这样可以保证将第一个高度不为0的建筑的起点加入结果集中。
vector<pair<int, int>> getSkyline(vector<vector<int>>& buildings) {
typedef pair<int, int> Event;
// events, x, h
vector<Event> es;
hs_.clear();
for (const auto& b : buildings) {
es.emplace_back(b[0], b[2]);
es.emplace_back(b[1], -b[2]);
}
// Sort events by x
sort(es.begin(), es.end(), [](const Event& e1, const Event& e2){
if (e1.first == e2.first) return e1.second > e2.second;
return e1.first < e2.first;
});
vector<pair<int, int>> ans;
// Process all the events
for (const auto& e: es) {
int x = e.first;
bool entering = e.second > 0;
int h = abs(e.second);
if (entering) {
if (h > this->maxHeight())
ans.emplace_back(x, h);
hs_.insert(h);
} else {
hs_.erase(hs_.equal_range(h).first);
if (h > this->maxHeight())
ans.emplace_back(x, this->maxHeight());
}
}
return ans;
}
private:
int maxHeight() const {
if (hs_.empty()) return 0;
return *hs_.rbegin();
}
multiset<int> hs_;
https://leetcode.com/problems/the-skyline-problem/discuss/61192/Once-for-all-explanation-with-clean-Java-code(O(n2)time-O(n)-space)http://www.cnblogs.com/grandyang/p/4534586.html
要是非要在之前的题目中找一道类似的题,也就只有 Merge Intervals 合并区间了吧,但是与那题不同的是,这道题不是求被合并成的空间,而是求轮廓线的一些关键的转折点,这就比较复杂了,我们通过仔细观察题目中给的那个例子可以发现,要求的红点都跟每个小区间的左右区间点有密切的关系,而且进一步发现除了每一个封闭区间的最右边的结束点是楼的右边界点,其余的都是左边界点,而且每个红点的纵坐标都是当前重合处的最高楼的高度,但是在右边界的那个楼的就不算了。在网上搜了很多帖子,发现网友Brian Gordon的帖子图文并茂,什么动画渐变啊,横向扫描啊,简直叼到没朋友啊,但是叼到极致后就懒的一句一句的去读了,这里博主还是讲解另一位网友百草园的博客吧。这里用到了multiset数据结构,其好处在于其中的元素是按堆排好序的,插入新元素进去还是有序的,而且执行删除元素也可方便的将元素删掉。这里为了区分左右边界,将左边界的高度存为负数,建立左边界和负高度的pair,再建立右边界和高度的pair,存入数组中,都存进去了以后,给数组按照左边界排序,这样我们就可以按顺序来处理那些关键的节点了。我们要在multiset中放入一个0,这样在某个没有和其他建筑重叠的右边界上,我们就可以将封闭点存入结果res中。下面我们按顺序遍历这些关键节点,如果遇到高度为负值的pair,说明是左边界,那么将正高度加入multiset中,然后取出此时集合中最高的高度,即最后一个数字,然后看是否跟pre相同,这里的pre是上一个状态的高度,初始化为0,所以第一个左边界的高度绝对不为0,所以肯定会存入结果res中。接下来如果碰到了一个更高的楼的左边界的话,新高度存入multiset的话会排在最后面,那么此时cur取来也跟pre不同,可以将新的左边界点加入结果res。第三个点遇到绿色建筑的左边界点时,由于其高度低于红色的楼,所以cur取出来还是红色楼的高度,跟pre相同,直接跳过。下面遇到红色楼的右边界,此时我们首先将红色楼的高度从multiset中删除,那么此时cur取出的绿色楼的高度就是最高啦,跟pre不同,则可以将红楼的右边界横坐标和绿楼的高度组成pair加到结果res中,这样就成功的找到我们需要的拐点啦,后面都是这样类似的情况。当某个右边界点没有跟任何楼重叠的话,删掉当前的高度,那么multiset中就只剩0了,所以跟当前的右边界横坐标组成pair就是封闭点啦
http://www.cnblogs.com/easonliu/p/4531020.html
https://briangordon.github.io/2014/08/the-skyline-problem.html
Our final solution, then, in time, is as follows. First, sort the critical points. Then scan across the critical points from left to right. When we encounter the left edge of a rectangle, we add that rectangle to the heap with its height as the key. When we encounter the right edge of a rectangle, we remove that rectangle from the heap. (This requires keeping external pointers into the heap.) Finally, any time we encounter a critical point, after updating the heap we set the height of that critical point to the value peeked from the top of the heap.
https://discuss.leetcode.com/topic/22482/short-java-solution/4
However, there is a small thing that can be improved. pq.remove() is O(n) hence make it slower. I have modified it a little bit to use TreeMap instead of PriorityQueue and the run time is 2.5X faster.
public List<int[]> getSkyline(int[][] buildings) {
List<int[]> heights = new ArrayList<>();
for (int[] b: buildings) {
heights.add(new int[]{b[0], - b[2]});
heights.add(new int[]{b[1], b[2]});
}
Collections.sort(heights, (a, b) -> (a[0] == b[0]) ? a[1] - b[1] : a[0] - b[0]);
TreeMap<Integer, Integer> heightMap = new TreeMap<>(Collections.reverseOrder());
heightMap.put(0,1);
int prevHeight = 0;
List<int[]> skyLine = new LinkedList<>();
for (int[] h: heights) {
if (h[1] < 0) {
Integer cnt = heightMap.get(-h[1]);
cnt = ( cnt == null ) ? 1 : cnt + 1;
heightMap.put(-h[1], cnt);
} else {
Integer cnt = heightMap.get(h[1]);
if (cnt == 1) {
heightMap.remove(h[1]);
} else {
heightMap.put(h[1], cnt - 1);
}
}
int currHeight = heightMap.firstKey();
if (prevHeight != currHeight) {
skyLine.add(new int[]{h[0], currHeight});
prevHeight = currHeight;
}
}
return skyLine;
}However, there is a small thing that can be improved. pq.remove() is O(n) hence make it slower. I have modified it a little bit to use TreeMap instead of PriorityQueue and the run time is 2.5X faster.
The basic idea of this solutions is to find the critical points that change the max height among the buildings on the left
public List<int[]> getSkyline(int[][] buildings) {
List<int[]> res = new ArrayList<>();
List<int[]> height = new ArrayList<>(); // height list to store all buildings' heights
for (int[] b : buildings) {
height.add(new int[]{b[0], - b[2]}); // start of a building, height stored as negtive
height.add(new int[]{b[1], b[2]}); // end of a building, height stored as positive
}
Collections.sort(height, (a, b) -> (a[0] == b[0] ? a[1] - b[1] : a[0] - b[0])); // sort the height list
// a pq that stores all the encountered buildings' heights in descending order
PriorityQueue<Integer> pq = new PriorityQueue<>((a, b) -> (b - a));
pq.offer(0);
int preMax = 0;
for (int[] h : height) {
if (h[1] < 0) { // h[1] < 0, that means it meets a new building, so add it to pq
pq.offer(-h[1]);
} else { // h[1] >=0, that means it has reached the end of the building, so remove it from pq
pq.remove(h[1]);
}
// the current max height in all encountered buildings
int curMax = pq.peek();
// if the max height is different from the previous one, that means a critical point is met, add to result list
if (curMax != preMax) {
res.add(new int[]{h[0], curMax});
preMax = curMax;
}
}
return res;
}
https://discuss.leetcode.com/topic/26890/a-java-solution-by-iteratively-checking-the-starting-and-ending-points
https://discuss.leetcode.com/topic/28482/once-for-all-explanation-with-clean-java-code-o-n-2-time-o-n-space
Though I came up with a solution using PriorityQueue and BST, this problems still confuses me. To make it more clear, I went through it several times and investigated several good solutions on this forum.
Here is my explanation which tries to make understanding this easier and may help you write a bug-free solution quickly.
When visiting all start points and end points in order:
Observations:
- If a position is shadowed by other buildings
1. height of that building is larger than the building to which current position belong; 2. the start point of that building must be smaller(or equal to) than this position; 3. the end point of that building must be larger(or equal to) than this position;
Tus we have:
1. when you reach a start point, the height of current building immediately
takes effect which means it could possibly affect the contour or shadow
others when mixed with other following buildings;
2. when you reach a end point, the height of current building will stop its
influences;
3. our target exists at the position where height change happens and there
is nothing above it shadowing it;
Obviously, to implement the idea that 'current height takes effect' and 'find out whether current height is shadowed by other buildings', we need a mechanism to store current taking effect heights, meanwhile, figure out which one is the maximum, delete it if needed efficiently, which hints us to use a priority queue or BST.
Thus, our algorithm could be summarised in following pseudo code:
for position in sorted(all start points and all end points)
if this position is a start point
add its height
else if this position is a end point
delete its height
compare current max height with previous max height, if different, add
current position together with this new max height to our result, at the
same time, update previous max height to current max height;
To implement this algorithm, here are some concrete examples:
- In my implementation, I use a PriorityQueue to store end point values when visiting a start point, and store the [height, end point value] into a TreeMap. Thus:
- when moving to next start point value, I can compare the next start point value with elements in PriorityQueue, thus achieving visiting all start points and end points in order(exploits the fact that start points are already sorted);
- Meantime, I can get current max height from TreeMap in O(logn);
- However, to delete a height when visiting a end point, I have to use 'map.values.remove()' which is a method defined in Collection interface and tends to be slower(O(n) is this case, plz correct me if I'm wrong);
My code can be found at https://leetcode.com/discuss/62617/short-and-clean-java-solution-heap-and-treemap
- Following is wujin's implementation(plz refer to https://leetcode.com/discuss/54201/short-java-solution). This one is quite straightforward, clean and clever.
Firstly, please notice what we need to achieve:
1. visit all start points and all end points in order;
2. when visiting a point, we need to know whether it is a start point or a
end point, based on which we can add a height or delete a height from
our data structure;
To achieve this, his implementation:
1. use a int[][] to collect all [start point, - height] and [end point, height]
for every building;
2. sort it, firstly based on the first value, then use the second to break
ties;
Thus,
1. we can visit all points in order;
2. when points have the same value, higher height will shadow the lower one;
3. we know whether current point is a start point or a end point based on the
sign of its height;
如果按照一个矩形一个矩形来处理将会非常麻烦,我们可以把这些矩形拆成两个点,一个左上顶点,一个右上顶点。将所有顶点按照横坐标排序后,我们开始遍历这些点。遍历时,通过一个堆来得知当前图形的最高位置。堆顶是所有顶点中最高的点,只要这个点没被移出堆,说明这个最高的矩形还没结束。对于左顶点,我们将其加入堆中。对于右顶点,我们找出堆中其相应的左顶点,然后移出这个左顶点,同时也意味这这个矩形的结束。具体代码中,为了在排序后的顶点列表中区分左右顶点,左顶点的值是正数,而右顶点值则存的是负数。
- 堆中先加入一个零点高度,帮助我们在只有最矮的建筑物时选择最低值
public List<int[]> getSkyline(int[][] buildings) {
List<int[]> result = new ArrayList<>();
List<int[]> height = new ArrayList<>();
// 拆解矩形,构建顶点的列表
for(int[] b:buildings) {
// 左顶点存为负数
height.add(new int[]{b[0], -b[2]});
// 右顶点存为正数
height.add(new int[]{b[1], b[2]});
}
// 根据横坐标对列表排序,相同横坐标的点纵坐标小的排在前面
Collections.sort(height, new Comparator<int[]>(){
public int compare(int[] a, int[] b){
if(a[0] != b[0]){
return a[0] - b[0];
} else {
return a[1] - b[1];
}
}
});
// 构建堆,按照纵坐标来判断大小
Queue<Integer> pq = new PriorityQueue<Integer>(11, new Comparator<Integer>(){
public int compare(Integer i1, Integer i2){
return i2 - i1;
}
});
// 将地平线值9先加入堆中
pq.offer(0);
// prev用于记录上次keypoint的高度
int prev = 0;
for(int[] h:height) {
// 将左顶点加入堆中
if(h[1] < 0) {
pq.offer(-h[1]);
} else {
// 将右顶点对应的左顶点移去
pq.remove(h[1]);
}
int cur = pq.peek();
// 如果堆的新顶部和上个keypoint高度不一样,则加入一个新的keypoint
if(prev != cur) {
result.add(new int[]{h[0], cur});
prev = cur;
}
}
return result;
}
https://discuss.leetcode.com/topic/22482/short-java-solution
This problem is essentially a problem of processing 2*n edges. Each edge has a x-axis value and a height value. The key part is how to use the height heap to process each edge.
The problem looks quite tricky. It looks very like the segment intervals problem. For this kind of problems, one general solution is :
-- First, split the left key point and the right key point into two parts and store into another data structure. For this problem, [2 9 10] can be split into [2, 10, L] and [9, 10, R]
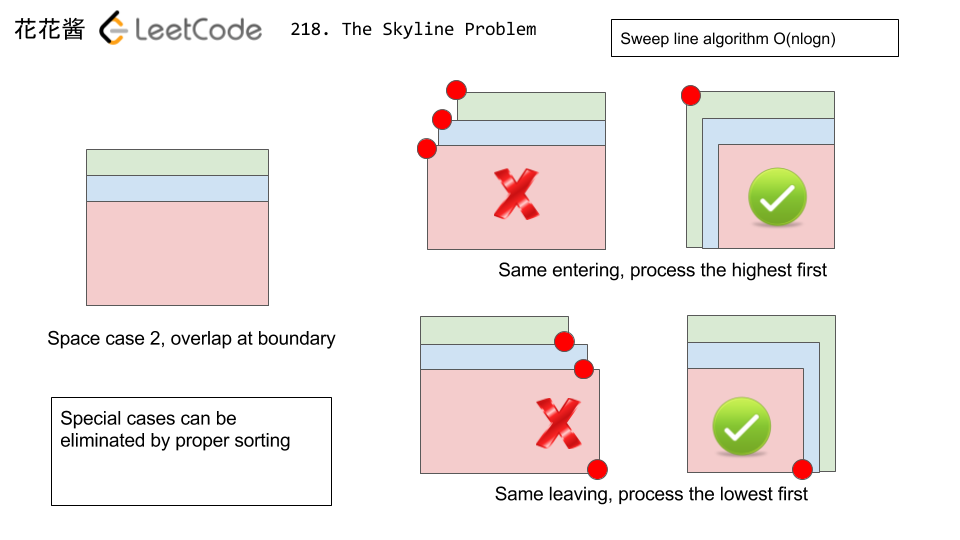
-- Then, sort the split list according to the x coordinate, if equal, sort by height. Note that for this problem, if two x coordinates are Left end, the greater height should be before the lower, because the lower height is hidden. If both are Right end, put the lower first.
-- Thirdly, iterate the sorted list. If the end point is left. Put into the priority queue. Note that if the priority queue is empty or the height of the end point is greater than the peek of the pq, put the end point into result list. If the end point is right. Remove the point from pq. If pq is empty then, put a <x, 0> into result list. Else, if the height of the end point is greater than the peek of the pq, put <x, peek()> into the result list.
-- First, split the left key point and the right key point into two parts and store into another data structure. For this problem, [2 9 10] can be split into [2, 10, L] and [9, 10, R]
-- Then, sort the split list according to the x coordinate, if equal, sort by height. Note that for this problem, if two x coordinates are Left end, the greater height should be before the lower, because the lower height is hidden. If both are Right end, put the lower first.
-- Thirdly, iterate the sorted list. If the end point is left. Put into the priority queue. Note that if the priority queue is empty or the height of the end point is greater than the peek of the pq, put the end point into result list. If the end point is right. Remove the point from pq. If pq is empty then, put a <x, 0> into result list. Else, if the height of the end point is greater than the peek of the pq, put <x, peek()> into the result list.
private class Edge { private int x; private int height; private boolean isLeft; // Constructor public Edge(int x, int height, boolean isLeft) { this.x = x; this.height = height; this.isLeft = isLeft; } } public List<int[]> getSkyline(int[][] buildings) { List<int[]> result = new ArrayList<int[]>(); if (buildings == null || buildings.length == 0 || buildings[0].length == 0) { return result; } PriorityQueue<Integer> pq = new PriorityQueue<>(1000, Collections.reverseOrder()); // Parse buildings and fill the edges List<Edge> edges = new ArrayList<Edge>(); for (int[] building : buildings) { Edge leftEdge = new Edge(building[0], building[2], true); edges.add(leftEdge); Edge rightEdge = new Edge(building[1], building[2], false); edges.add(rightEdge); } // Sort the edges according to the left keypoint Collections.sort(edges, new EdgeComparator()); // Iterate all sorted edges for (Edge edge : edges) { if (edge.isLeft) { if (pq.isEmpty() || edge.height > pq.peek()) { result.add(new int[]{edge.x, edge.height}); } pq.offer(edge.height); } else { pq.remove(edge.height); // bad, O(n) to remove if (pq.isEmpty()) { result.add(new int[]{edge.x, 0}); } else if (edge.height > pq.peek()) { result.add(new int[]{edge.x, pq.peek()}); } } } return result; } public class EdgeComparator implements Comparator<Edge> { @Override public int compare(Edge a, Edge b) { if (a.x != b.x) { return a.x - b.x; } if (a.isLeft && b.isLeft) { return b.height - a.height; } if (!a.isLeft && !b.isLeft) { return a.height - b.height; } return a.isLeft ? -1 : 1; } }
An alternative solution:
http://codechen.blogspot.com/2015/06/leetcode-skyline-problem.html
http://www.cnblogs.com/easonliu/p/4531020.html
把每一个building拆成两个edge,一个入一个出。所有的edge加入到一个list中。再对这个list进行排序,排序顺序为:如果两个边的position不一样,那么按pos排,否则根据edge是入还是出来排。
Notice that "key points" are either the left or right edges of the buildings. Therefore, we first obtain both the edges of all the N buildings, and store the 2N edges in a sorted array. Maintain a max-heap of building heights while scanning through the edge array: If the current edge is a left edge, then add the height of its associated building to the max-heap; if the edge is a right one, remove the associated height from the heap. Then we take the top value of the heap (yi) as the maximum height at the current edge position (xi). Now (xi, yi) is a potential key point. If yi is the same as the height of the last key point in the result list, it means that this key point is not a REAL key point, but rather a horizontal continuation of the last point, so it should be discarded; otherwise, we add (xi,yi) to the result list because it is a real key point. Repeat this process until all the edges are checked.
It takes O(NlogN) time to sort the edge array. For each of the 2N edges, it takes O(1) time to query the maximum height but O(logN) time to add or remove elements. Overall, this solution takes O(NlogN) time.
X. http://blog.welkinlan.com/2015/09/29/the-skyline-problem-leetcode-java/Construct a HeightLine class to store each edge, with height < 0 indicating the left edge, height > 0 indicating the right edge.Sort the edges by index and height, the tricky part is when h1.index == h2.index, we have three cases:
- h1 and h2 are both left edge (height < 0): the higher line should be sorted before the lower line (for e.g., |h1.height| > |h2.height| => h1.height – h2.height < 0 => h1 will be sorted before h2)
- h1 and h2 are both right edge (height >0): the lower line should be sorted before the higher line (for e.g., h1.height – h2.height < 0 => h1 will be sorted before h2)
- One left edge (<0) and One right edge (>0): left should be sorted before right (for e.g., h1 is left and h2 is right => h1.height – h2.height < 0 => h1 will be sorted before h2)
Thus we can safely use h1.height – h2.height as the return value of compare() functionOffer / Delete the sorted edges one by one into a Max-heap, which store the heights of all the valid buildings to the current index. Check if offering / deleting a new edge will update the peek(): if it is, we find a new skyline and add it to the result.
http://www.cnblogs.com/easonliu/p/4531020.html
(1) 自建一个名为Height的数据结构,保存一个building的index和height。约定,当height为负数时表示这个高度为height的building起始于index;height为正时表示这个高度为height的building终止于index。
(2) 对building数组进行处理,每一行[ Li, Ri, Hi ],根据Height的定义,转换为两个Height的对象,即,Height(Li, -Hi) 和 Height(Ri, Hi)。 将这两个对象存入heights这个List中。
(3) 写个Comparator对heights进行升序排序,首先按照index的大小排序,若index相等,则按height大小排序,以保证一栋建筑物的起始节点一定在终止节点之前。
(4) 将heights转换为结果。使用PriorityQueue对高度值进行暂存。遍历heights,遇到高度为负值的对象时,表示建筑物的起始节点,此时应将这个高度加入PriorityQueue。遇到高度为正值的对象时,表示建筑物的终止节点,此时应将这个高度从PriorityQueue中除去。且在遍历的过程中检查,当前的PriorityQueue的peek()是否与上一个iteration的peek()值(prev)相同,若否,则应在结果中加入[当前对象的index, 当前PriorityQueue的peek()],并更新prev的值。
public List<int[]> getSkyline(int[][] buildings) {
List<int[]> result = new ArrayList<int[]>();
if (buildings == null || buildings.length == 0 || buildings[0].length == 0) {
return result;
}
List<Height> heights = new ArrayList<Height>();
for (int[] building : buildings) {
heights.add(new Height(building[0], -building[2]));
heights.add(new Height(building[1], building[2]));
}
Collections.sort(heights, new Comparator<Height>() {
@Override
public int compare(Height h1, Height h2) {
return h1.index != h2.index ? h1.index - h2.index : h1.height - h2.height;
}
});
PriorityQueue<Integer> pq = new PriorityQueue<Integer>(1000, Collections.reverseOrder());
pq.offer(0);
int prev = 0;
for (Height h : heights) {
if (h.height < 0) {
pq.offer(-h.height);
} else {
pq.remove(h.height);
}
int cur = pq.peek();
if (cur != prev) {
result.add(new int[]{h.index, cur});
prev = cur;
}
}
return result;
}
class Height {
int index;
int height;
Height(int index, int height) {
this.index = index;
this.height = height;
}
}根据position从前到后扫描每一个edge,将edge根据是入还是出来将当前height加入或者移除heap。再得到当前最高点来决定是否加入最终结果。
public List<int[]> getSkyline(int[][] buildings) { List<int[]> res = new ArrayList<int[]>(); if (buildings == null || buildings.length == 0 || buildings[0].length == 0) { return res; } List<Edge> edges = new ArrayList<Edge>(); for (int[] building : buildings) { Edge startEdge = new Edge(building[0], building[2], true); edges.add(startEdge); Edge endEdge = new Edge(building[1], building[2], false); edges.add(endEdge); } //sort edges according to position, height, and if the edge is start or end edges.sort(new Comparator<Edge>(){ public int compare(Edge l1, Edge l2) { if (l1.pos != l2.pos) return Integer.compare(l1.pos, l2.pos); if (l1.isStart && l2.isStart) { return Integer.compare(l2.height, l1.height); } if (!l1.isStart && !l2.isStart) { return Integer.compare(l1.height, l2.height); } return l1.isStart ? -1 : 1; } }); //heap of height PriorityQueue<Integer> heap = new PriorityQueue<Integer>(10, Collections.reverseOrder()); for (Edge edge : edges) { if (edge.isStart) { if (heap.isEmpty() || edge.height > heap.peek()) { res.add(new int[]{edge.pos, edge.height}); } heap.add(edge.height); } else { heap.remove(edge.height); if (heap.isEmpty() || edge.height > heap.peek()) { res.add(heap.isEmpty() ? new int[]{edge.pos,0} : new int[]{edge.pos, heap.peek()}); } } } return res; } class Edge implements Comparable<Edge>{ int pos; int height; boolean isStart; public Edge(int pos, int height, boolean isStart) { this.pos = pos; this.height = height; this.isStart = isStart; } }https://discuss.leetcode.com/topic/16511/share-my-divide-and-conquer-java-solution-464-ms
http://www.geeksforgeeks.org/divide-and-conquer-set-7-the-skyline-problem/
public List<int[]> getSkyline(int[][] buildings) {
if (buildings.length == 0)
return new LinkedList<int[]>();
return recurSkyline(buildings, 0, buildings.length - 1);
}
private LinkedList<int[]> recurSkyline(int[][] buildings, int p, int q) {
if (p < q) {
int mid = p + (q - p) / 2;
return merge(recurSkyline(buildings, p, mid),
recurSkyline(buildings, mid + 1, q));
} else {
LinkedList<int[]> rs = new LinkedList<int[]>();
rs.add(new int[] { buildings[p][0], buildings[p][2] });
rs.add(new int[] { buildings[p][1], 0 });
return rs;
}
}
private LinkedList<int[]> merge(LinkedList<int[]> l1, LinkedList<int[]> l2) {
LinkedList<int[]> rs = new LinkedList<int[]>();
int h1 = 0, h2 = 0;
while (l1.size() > 0 && l2.size() > 0) {
int x = 0, h = 0;
if (l1.getFirst()[0] < l2.getFirst()[0]) {
x = l1.getFirst()[0];
h1 = l1.getFirst()[1];
h = Math.max(h1, h2);
l1.removeFirst();
} else if (l1.getFirst()[0] > l2.getFirst()[0]) {
x = l2.getFirst()[0];
h2 = l2.getFirst()[1];
h = Math.max(h1, h2);
l2.removeFirst();
} else {
x = l1.getFirst()[0];
h1 = l1.getFirst()[1];
h2 = l2.getFirst()[1];
h = Math.max(h1, h2);
l1.removeFirst();
l2.removeFirst();
}
if (rs.size() == 0 || h != rs.getLast()[1]) {
rs.add(new int[] { x, h });
}
}
rs.addAll(l1);
rs.addAll(l2);
return rs;
}
解法一:总体思想是Divide and Conquer,但是Conquer的时候需要特殊处理左边重叠的情况。Merge的基本思路是设两个变量h1 = 0, h2 = 0,以及maxH用于记录上次的高度。取两个序列中x小的,相应的改变h1或h2的值。同时merge后的新元素为(x.min, max(h1, h2)),并且只有当max(h1,h2) != maxH的时候才更新,这样可以防止添加进高度一样的元素。然后令maxH = max(h1, h2)保存当次的高度值,用于下次更新时的比较。
- public List<int[]> getSkyline(int[][] buildings) {
- List<int[]> results = new ArrayList<>();
- if(buildings.length == 0)
- return results;
- if(buildings.length == 1) {
- results.add(new int[]{buildings[0][0], buildings[0][2]});
- results.add(new int[]{buildings[0][1], 0});
- return results;
- }
- int mid = (buildings.length - 1) / 2;
- List<int[]> left = divide(0, mid, buildings);
- List<int[]> right = divide(mid + 1, buildings.length - 1, buildings);
- results = conquer(left, right);
- return results;
- }
- List<int[]> divide(int start, int end, int[][] buildings) {
- List<int[]> result = new ArrayList<>();
- if(start == end) {
- result.add(new int[]{buildings[start][0], buildings[start][2]});
- result.add(new int[]{buildings[start][1], 0});
- return result;
- }
- int mid = (start + end) / 2;
- List<int[]> left = divide(start, mid, buildings);
- List<int[]> right = divide(mid + 1, end, buildings);
- result = conquer(left, right);
- return result;
- }
- List<int[]> conquer(List<int[]> left, List<int[]> right) {
- List<int[]> result = new ArrayList<>();
- int i = 0, j = 0;
- int h1 = 0, h2 = 0;
- int maxH = 0;
- while(i < left.size() && j < right.size()) {
- if(left.get(i)[0] < right.get(j)[0]) {
- h1 = left.get(i)[1];
- if(maxH != Math.max(h1, h2)) {
- result.add(new int[]{left.get(i)[0], Math.max(h1, h2)});
- }
- maxH = Math.max(h1, h2);
- i++;
- } else if(left.get(i)[0] > right.get(j)[0]) {
- h2 = right.get(j)[1];
- if(maxH != Math.max(h1, h2)) {
- result.add(new int[]{right.get(j)[0], Math.max(h1, h2)});
- }
- maxH = Math.max(h1, h2);
- j++;
- } else {
- h1 = left.get(i)[1];
- h2 = right.get(j)[1];
- if(maxH != Math.max(h1, h2))
- result.add(new int[]{left.get(i)[0], Math.max(h1, h2)});
- maxH = Math.max(h1, h2);
- i++;
- j++;
- }
- }
- while(i < left.size()) {
- result.add(new int[]{left.get(i)[0], left.get(i)[1]});
- i++;
- }
- while(j < right.size()) {
- result.add(new int[]{right.get(j)[0], right.get(j)[1]});
- j++;
- }
- return result;
- }
- }
A Simple Solution is to initialize skyline or result as empty, then one by one add buildings to skyline. A building is added by first finding the overlapping strip(s). If there are no overlapping strips, the new building adds new strip(s). If overlapping strip is found, then height of the existing strip may increase. Time complexity of this solution is O(n2)
We can find Skyline in Θ(nLogn) time using Divide and Conquer. The idea is similar to Merge Sort, divide the given set of buildings in two subsets. Recursively construct skyline for two halves and finally merge the two skylines.
How to Merge two Skylines?
The idea is similar to merge of merge sort, start from first strips of two skylines, compare x coordinates. Pick the strip with smaller x coordinate and add it to result. The height of added strip is considered as maximum of current heights from skyline1 and skyline2.
The idea is similar to merge of merge sort, start from first strips of two skylines, compare x coordinates. Pick the strip with smaller x coordinate and add it to result. The height of added strip is considered as maximum of current heights from skyline1 and skyline2.
https://leetcode.com/discuss/48638/java-570ms-430ms-divide-conquer-solution-with-explanation
DrawingSkylines.java
public static class Skyline {
public int left, right, height;
public Skyline(int left, int right, int height) {
this.left = left;
this.right = right;
this.height = height;
}
}
public static List<Skyline> drawingSkylines(List<Skyline> skylines) {
return drawingSkylinesHelper(skylines, 0, skylines.size());
}
private static List<Skyline> drawingSkylinesHelper(List<Skyline> skylines,
int start, int end) {
if (end - start <= 1) { // 0 or 1 skyline, just copy it.
return new ArrayList<>(skylines.subList(start, end));
}
int mid = start + ((end - start) / 2);
List<Skyline> L = drawingSkylinesHelper(skylines, start, mid);
List<Skyline> R = drawingSkylinesHelper(skylines, mid, end);
return mergeSkylines(L, R);
}
private static List<Skyline> mergeSkylines(List<Skyline> L, List<Skyline> R) {
int i = 0, j = 0;
List<Skyline> merged = new ArrayList<>();
while (i < L.size() && j < R.size()) {
if (L.get(i).right < R.get(j).left) {
merged.add(L.get(i++));
} else if (R.get(j).right < L.get(i).left) {
merged.add(R.get(j++));
} else if (L.get(i).left <= R.get(j).left) {
Ref<Integer> iWrapper = new Ref<>(i);
Ref<Integer> jWrapper = new Ref<>(j);
mergeIntersectSkylines(merged, L.get(i), iWrapper, R.get(j), jWrapper);
i = iWrapper.value;
j = jWrapper.value;
} else { // L.get(i).left > R.get(j).left.
Ref<Integer> iWrapper = new Ref<>(i);
Ref<Integer> jWrapper = new Ref<>(j);
mergeIntersectSkylines(merged, R.get(j), jWrapper, L.get(i), iWrapper);
i = iWrapper.value;
j = jWrapper.value;
}
}
merged.addAll(L.subList(i, L.size()));
merged.addAll(R.subList(j, R.size()));
return merged;
}
private static void mergeIntersectSkylines(List<Skyline> merged, Skyline a,
Ref<Integer> aIdx, Skyline b,
Ref<Integer> bIdx) {
if (a.right <= b.right) {
if (a.height > b.height) {
if (b.right != a.right) {
merged.add(a);
aIdx.value = aIdx.value + 1;
b.left = a.right;
} else {
bIdx.value = bIdx.value + 1;
}
} else if (a.height == b.height) {
b.left = a.left;
aIdx.value = aIdx.value + 1;
} else { // a->height < b->height.
if (a.left != b.left) {
merged.add(new Skyline(a.left, b.left, a.height));
}
aIdx.value = aIdx.value + 1;
}
} else { // a.right > b.right.
if (a.height >= b.height) {
bIdx.value = bIdx.value + 1;
} else {
if (a.left != b.left) {
merged.add(new Skyline(a.left, b.left, a.height));
}
a.left = b.right;
merged.add(b);
bIdx.value = bIdx.value + 1;
}
}
}
https://leijiangcoding.wordpress.com/2015/05/27/leetcode-q218-the-skyline-problem/
http://www.shuatiblog.com/blog/2014/07/01/The-Skyline-Problem/
Maximum Heap
把所有的turning points 放在一起,根据coordination从小到大sort 。
再用max-heap, 把所有的turning points扫一遍,遇到start turning point, 把 volume放入max-heap. 遇到end turning point,把对应的volume从max-heap中取出。
max-heap的max 值就是对应区间的最大volume
https://leetcode.com/problems/the-skyline-problem/discuss/61230/java-segment-tree-solution-47-ms
X. Binary Index Trees
https://leetcode.com/problems/the-skyline-problem/discuss/61198/My-O(nlogn)-solution-using-Binary-Indexed-Tree(BIT)Fenwick-Tree
Brute force:
https://discuss.leetcode.com/topic/14812/my-o-nlogn-solution-using-binary-indexed-tree-bit-fenwick-tree
http://www.shuatiblog.com/blog/2014/07/01/The-Skyline-Problem/
Maximum Heap
把所有的turning points 放在一起,根据coordination从小到大sort 。
再用max-heap, 把所有的turning points扫一遍,遇到start turning point, 把 volume放入max-heap. 遇到end turning point,把对应的volume从max-heap中取出。
max-heap的max 值就是对应区间的最大volume
public int[] skyline(List<Building> bds, int min, int max) {
int[] output = new int[max - min];
List<Edge>[] edges = new List[max - min];
for (int i = 0; i < edges.length; i++) {
edges[i] = new ArrayList<Edge>();
}
for (Building b : bds) {
// put all edges into an array of edges
edges[b.from].add(new Edge(b, true));
edges[b.to].add(new Edge(b, false));
}
Queue<Building> heap = new PriorityQueue<Building>(100,
new Comparator<Building>() {
public int compare(Building b1, Building b2) {
return b2.height - b1.height;
}
});
for (int i = 0; i < edges.length; i++) {
// insert or remove each building at position i into max heap
for (Edge e : edges[i]) {
if (e.isEnter) {
heap.add(e.building);
} else {
heap.remove(e.building);
}
}
// then culculate the current hight, which is top of the heap
if (!heap.isEmpty()) {
output[i] = heap.peek().height;
}
}
return output;
}
static class Edge {
Building building;
boolean isEnter;
}
static class Building {
int from;
int to;
int height;
}https://leetcode.com/problems/the-skyline-problem/discuss/61230/java-segment-tree-solution-47-ms
private static class Node{
int start, end;
Node left, right;
int height;
public Node(int start, int end){
this.start = start;
this.end = end;
}
}
public List<int[]> getSkyline(int[][] buildings) {
Set<Integer> endpointSet = new HashSet<Integer>();
for(int[] building : buildings){
endpointSet.add(building[0]);
endpointSet.add(building[1]);
}
List<Integer> endpointList = new ArrayList<Integer>(endpointSet);
Collections.sort(endpointList);
HashMap<Integer, Integer> endpointMap = new HashMap<Integer, Integer>();
for(int i = 0; i < endpointList.size(); i++){
endpointMap.put(endpointList.get(i), i);
}
Node root = buildNode(0, endpointList.size() - 1);
for(int[] building : buildings){
add(root, endpointMap.get(building[0]), endpointMap.get(building[1]), building[2]);
}
List<int[]> result = new ArrayList<int[]>();
explore(result, endpointList, root);
if(endpointList.size() > 0){
result.add(new int[]{endpointList.get(endpointList.size() - 1), 0});
}
return result;
}
private Node buildNode(int start, int end){
if(start > end){
return null;
}else{
Node result = new Node(start, end);
if(start + 1 < end){
int center = start + (end - start) / 2;
result.left = buildNode(start, center);
result.right = buildNode(center, end);
}
return result;
}
}
private void add(Node node, int start, int end, int height){
if(node == null || start >= node.end || end <= node.start || height < node.height){
return;
}else{
if(node.left == null && node.right == null){
node.height = Math.max(node.height, height);
}else{
add(node.left, start, end, height);
add(node.right, start, end, height);
node.height = Math.min(node.left.height, node.right.height);
}
}
}
private void explore(List<int[]> result, List<Integer> endpointList, Node node){
if(node == null){
return;
}else{
if(node.left == null && node.right == null && (result.size() == 0 || result.get(result.size() - 1)[1] != node.height)){
result.add(new int[]{endpointList.get(node.start), node.height});
}else{
explore(result, endpointList, node.left);
explore(result, endpointList, node.right);
}
}
}X. Binary Index Trees
https://leetcode.com/problems/the-skyline-problem/discuss/61198/My-O(nlogn)-solution-using-Binary-Indexed-Tree(BIT)Fenwick-Tree
public List<int[]> getSkyline(int[][] buildings) {
List<int[]> ret = new ArrayList<>();
if (buildings.length==0) return ret;
List<int[]> points = new ArrayList<>();
for (int i=0;i<buildings.length;i++) {
int[] b = buildings[i];
points.add(new int[]{b[0], 1, i});
points.add(new int[]{b[1], 2, i});
}
Collections.sort(points, (a,b)->a[0]==b[0]?a[1]-b[1]: a[0]-b[0]);
// binary indexed tree
// stores the max height for each segment, bit[i] is the max height of segment between point i-1 and i
int[] bit = new int[points.size()+1];
Map<Integer, Integer> index = new HashMap<>();
for (int i=0;i<points.size();i++) {
index.putIfAbsent(points.get(i)[0], i);
}
int prevHeight = -1;
for (int i=0;i<points.size();i++) {
int[] pt = points.get(i);
if (pt[1]==1) {
// start of a building
// put height in scope, scope ends when building end
int[] building=buildings[pt[2]];
add(bit, index.get(building[1]), building[2]);
}
int cur = find(bit, index.get(pt[0])+1);
if (cur!=prevHeight) {
if (ret.size()>0 && ret.get(ret.size()-1)[0]==pt[0]) {
ret.get(ret.size()-1)[1] = Math.max(cur, ret.get(ret.size()-1)[1]);
} else {
ret.add(new int[]{pt[0], cur});
}
prevHeight=cur;
}
}
return ret;
}
void add(int[] bit, int i, int h) {
while (i>0) {
bit[i]=Math.max(bit[i], h);
i-=(i&-i);
}
}
int find(int[] bit, int i) {
int h=0;
while (i<bit.length) {
h=Math.max(h, bit[i]);
i+=(i&-i);
}
return h;
}Brute force:
https://discuss.leetcode.com/topic/14812/my-o-nlogn-solution-using-binary-indexed-tree-bit-fenwick-tree
we can use Binary Indexed Tree(BIT)/Fenwick Tree to solve this problem, the (Value and (Value xor (Value - 1))), O(nlogn) Solution: