Quadtree

http://en.wikipedia.org/wiki/Quadtree

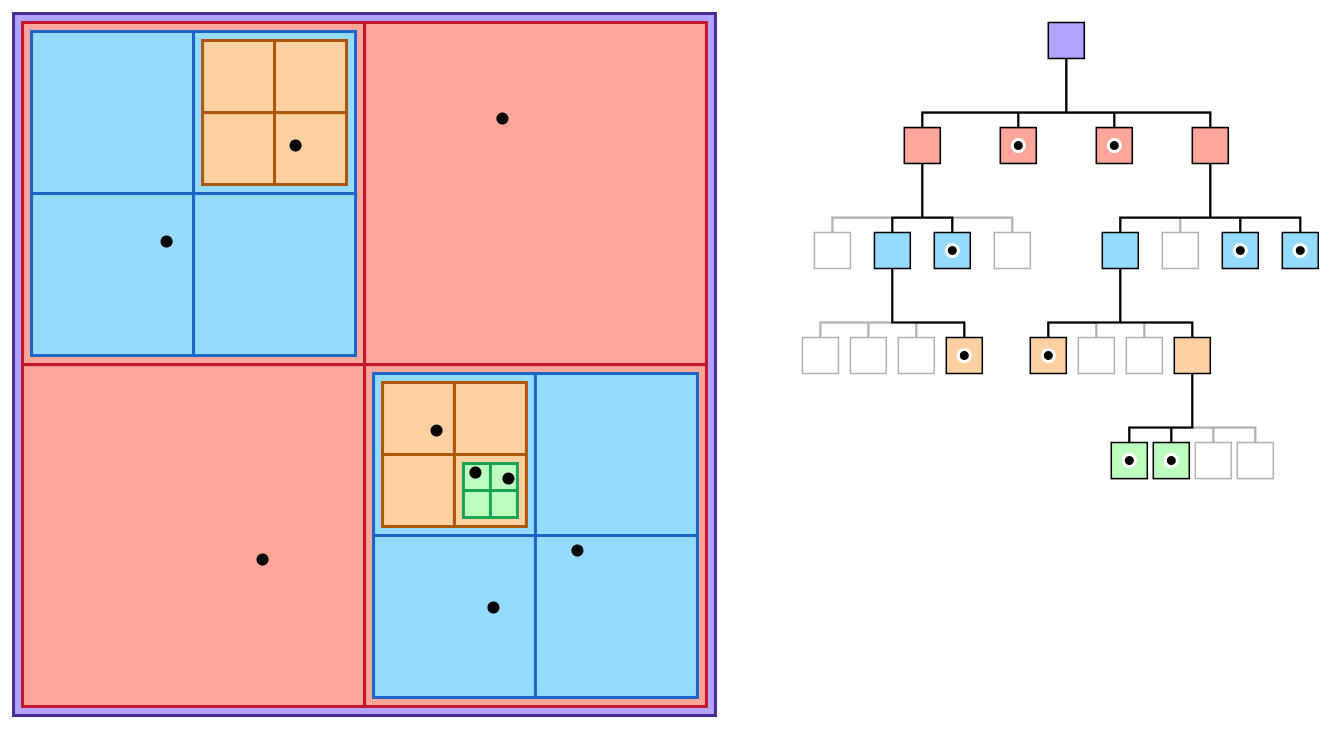
A quadtree is a tree data structure in which each internal node has exactly four children. Quadtrees are most often used to partition a two-dimensional space by recursively subdividing it into four quadrants or regions. The regions may be square or rectangular, or may have arbitrary shapes. 

A similar partitioning is also known as a Q-tree. All forms of quadtrees share some common features:

• They decompose space into adaptable cells
• Each cell (or bucket) has a maximum capacity. When maximum capacity is reached, the bucket splits
• The tree directory follows the spatial decomposition of the quadtree.

http://algs4.cs.princeton.edu/92search/QuadTree.java.html

public class QuadTree<Key extends Comparable<Key>, Value>  {
    private Node root;

    // helper node data type
    private class Node {
        Key x, y;              // x- and y- coordinates
        Node NW, NE, SE, SW;   // four subtrees
        Value value;           // associated data

        Node(Key x, Key y, Value value) {
            this.x = x;
            this.y = y;
            this.value = value;
        }
    }


  /***********************************************************************
    *  Insert (x, y) into appropriate quadrant
    ***************************************************************************/
    public void insert(Key x, Key y, Value value) {
        root = insert(root, x, y, value);
    }

    private Node insert(Node h, Key x, Key y, Value value) {
        if (h == null) return new Node(x, y, value);
        //// if (eq(x, h.x) && eq(y, h.y)) h.value = value;  // duplicate
        else if ( less(x, h.x) &&  less(y, h.y)) h.SW = insert(h.SW, x, y, value);
        else if ( less(x, h.x) && !less(y, h.y)) h.NW = insert(h.NW, x, y, value);
        else if (!less(x, h.x) &&  less(y, h.y)) h.SE = insert(h.SE, x, y, value);
        else if (!less(x, h.x) && !less(y, h.y)) h.NE = insert(h.NE, x, y, value);
        return h;
    }


  /***********************************************************************
    *  Range search.
    ***************************************************************************/

    public void query2D(Interval2D<Key> rect) {
        query2D(root, rect);
    }

    private void query2D(Node h, Interval2D<Key> rect) {
        if (h == null) return;
        Key xmin = rect.intervalX.low;
        Key ymin = rect.intervalY.low;
        Key xmax = rect.intervalX.high;
        Key ymax = rect.intervalY.high;
        if (rect.contains(h.x, h.y))
            StdOut.println("    (" + h.x + ", " + h.y + ") " + h.value);
        if ( less(xmin, h.x) &&  less(ymin, h.y)) query2D(h.SW, rect);
        if ( less(xmin, h.x) && !less(ymax, h.y)) query2D(h.NW, rect);
        if (!less(xmax, h.x) &&  less(ymin, h.y)) query2D(h.SE, rect);
        if (!less(xmax, h.x) && !less(ymax, h.y)) query2D(h.NE, rect);
    }


   /***************************************************************************
    *  helper comparison functions
    ***************************************************************************/

    private boolean less(Key k1, Key k2) { return k1.compareTo(k2) <  0; }
    private boolean eq  (Key k1, Key k2) { return k1.compareTo(k2) == 0; }
}

http://gamedevelopment.tutsplus.com/tutorials/quick-tip-use-quadtrees-to-detect-likely-collisions-in-2d-space--gamedev-374

public class Quadtree {

  private int MAX_OBJECTS = 10;

  private int MAX_LEVELS = 5;

  private int level;

  private List objects;

  private Rectangle bounds;

  private Quadtree[] nodes;

 /*

  * Constructor

  */

  public Quadtree(int pLevel, Rectangle pBounds) {

   level = pLevel;

   objects = new ArrayList();

   bounds = pBounds;

   nodes = new Quadtree[4];

  }

}

/*

 * Splits the node into 4 subnodes

 */

 private void split() {

   int subWidth = (int)(bounds.getWidth() / 2);

   int subHeight = (int)(bounds.getHeight() / 2);

   int x = (int)bounds.getX();

   int y = (int)bounds.getY();

   nodes[0] = new Quadtree(level+1, new Rectangle(x + subWidth, y, subWidth, subHeight));

   nodes[1] = new Quadtree(level+1, new Rectangle(x, y, subWidth, subHeight));

   nodes[2] = new Quadtree(level+1, new Rectangle(x, y + subHeight, subWidth, subHeight));

   nodes[3] = new Quadtree(level+1, new Rectangle(x + subWidth, y + subHeight, subWidth, subHeight));

 }

 public void insert(Rectangle pRect) {

   if (nodes[0] != null) {

     int index = getIndex(pRect);

     if (index != -1) {

       nodes[index].insert(pRect);

       return;

     }

   }

   objects.add(pRect);

   if (objects.size() > MAX_OBJECTS && level < MAX_LEVELS) {

      if (nodes[0] == null) {

         split();

      }

     int i = 0;

     while (i < objects.size()) {

       int index = getIndex(objects.get(i));

       if (index != -1) {

         nodes[index].insert(objects.remove(i));

       }

       else {

         i++;

       }

     }

   }

 }

http://blog.notdot.net/2009/11/Damn-Cool-Algorithms-Spatial-indexing-with-Quadtrees-and-Hilbert-Curves

https://developer.apple.com/documentation/gameplaykit/gkquadtree

The quadtree partitioning strategy divides space into four quadrants at each level, as illustrated in Figure 1. When a quadrant contains more than one object, the tree subdivides that region into four smaller quadrants, adding a level to the tree.

Figure 1 

Spatial and logical arrangement of an example quadtree

http://blog.notdot.net/2009/11/Damn-Cool-Algorithms-Spatial-indexing-with-Quadtrees-and-Hilbert-Curves