https://leetcode.com/articles/longest-palindromic-substring/
Also check http://massivealgorithms.blogspot.com/2014/06/leetcode-longest-palindromic-substring.html
You might be asking why there are 2N-1 but not N centers? The reason is the center of a palindrome can be in between two letters. Such palindromes have even number of letters (such as “abba”) and its center are between the two ‘b’s.
22 // Given a center, either one letter or two letter, 23 // Find longest palindrome
24 public String helper(String s, int begin, int end) {
25 while (begin >= 0 && end <= s.length() - 1 && s.charAt(begin) == s.charAt(end)) {
26 begin--;
27 end++;
28 }
29 return s.substring(begin + 1, end);
30 }
https://leetcode.com/discuss/23848/easy-java-solution-with-o-1-space-and-o-n-2-time
StringBuilder longest = new StringBuilder(""); public String longestPalindrome(String s) { if (s.length() <= 1) return s; for (int i = 0; i < s.length(); i++) { expand(s, longest, i, i); //odd expand(s, longest, i, i + 1); //even } return longest.toString(); } private void expand(String s, StringBuilder longest, int i, int j) { while (i >= 0 && j < s.length()) { if (s.charAt(i) == s.charAt(j)) { if (j - i + 1 > longest.length()) { longest.delete(0, longest.length()); // use setLength(0) longest.append(s.substring(i, j + 1)); } i--; j++; } else break; } }
a modified version without StringBuiler - save the i, j position.
private int maxLength = 1; private int maxIndex = 0; public String longestPalindrome(String str) { //O(N^2), space O(1) int length = str.length(); for (int i=0; i<length; i++) { // find longest odd palindrome with center i findPalindrome(str, length, i, 0); // find longest even palindrome with center i findPalindrome(str, length, i, 1); } return str.substring(maxIndex, maxIndex+maxLength); } private void findPalindrome(String str, int length, int i, int shift) { int left = i; int right= i+shift; while (left >= 0 && right < length && str.charAt(left) == str.charAt(right)) { if ((right - left + 1) > maxLength) { maxLength = right - left + 1; maxIndex = left; } left--; right++; } }
http://www.programcreek.com/2013/12/leetcode-solution-of-longest-palindromic-substring-java/
X. DPTime O(n^2) Space O(n^2)
Also check http://massivealgorithms.blogspot.com/2014/06/leetcode-longest-palindromic-substring.html
Given a string s, find the longest palindromic substring in s. You may assume that the maximum length of s is 1000.
Example:
Input: "babad" Output: "bab" Note: "aba" is also a valid answer.
Example:
Input: "cbbd" Output: "bb"
You might be asking why there are 2N-1 but not N centers? The reason is the center of a palindrome can be in between two letters. Such palindromes have even number of letters (such as “abba”) and its center are between the two ‘b’s.
Since expanding a palindrome around its center could take O(N) time, the overall complexity is O(N2).
X. Expand
https://leetcode.com/problems/longest-palindromic-substring/discuss/2928/very-simple-clean-java-solution
http://www.cnblogs.com/springfor/p/3889209.html
private int lo, maxLen;
public String longestPalindrome(String s) {
int len = s.length();
if (len < 2)
return s;
for (int i = 0; i < len-1; i++) {
extendPalindrome(s, i, i); //assume odd length, try to extend Palindrome as possible
extendPalindrome(s, i, i+1); //assume even length.
}
return s.substring(lo, lo + maxLen);
}
private void extendPalindrome(String s, int j, int k) {
while (j >= 0 && k < s.length() && s.charAt(j) == s.charAt(k)) {
j--;
k++;
}
if (maxLen < k - j - 1) {
lo = j + 1;
maxLen = k - j - 1;
}http://www.cnblogs.com/springfor/p/3889209.html
第二种方法“是对于每个子串的中心(可以是一个字符,或者是两个字符的间隙,比如串abc,中心可以是a,b,c,或者是ab的间隙,bc的间隙,例如aba是回文,abba也是回文,这两种情况要分情况考虑)往两边同时进 行扫描,直到不是回文串为止。假设字符串的长度为n,那么中心的个数为2*n-1(字符作为中心有n个,间隙有n-1个)。对于每个中心往两边扫描的复杂 度为O(n),所以时间复杂度为O((2*n-1)*n)=O(n^2),空间复杂度为O(1)。”
string expandAroundCenter(string s, int c1, int c2) {
int l = c1, r = c2;
int n = s.length();
while (l >= 0 && r <= n-1 && s[l] == s[r]) {
l--;
r++;
}
return s.substr(l+1, r-l-1);
}
string longestPalindromeSimple(string s) {
int n = s.length();
if (n == 0) return "";
string longest = s.substr(0, 1); // a single char itself is a palindrome
for (int i = 0; i < n-1; i++) {
string p1 = expandAroundCenter(s, i, i);
if (p1.length() > longest.length())
longest = p1;
string p2 = expandAroundCenter(s, i, i+1);
if (p2.length() > longest.length())
longest = p2;
}
return longest;
}
22 // Given a center, either one letter or two letter, 23 // Find longest palindrome
24 public String helper(String s, int begin, int end) {
25 while (begin >= 0 && end <= s.length() - 1 && s.charAt(begin) == s.charAt(end)) {
26 begin--;
27 end++;
28 }
29 return s.substring(begin + 1, end);
30 }
https://leetcode.com/discuss/23848/easy-java-solution-with-o-1-space-and-o-n-2-time
StringBuilder longest = new StringBuilder(""); public String longestPalindrome(String s) { if (s.length() <= 1) return s; for (int i = 0; i < s.length(); i++) { expand(s, longest, i, i); //odd expand(s, longest, i, i + 1); //even } return longest.toString(); } private void expand(String s, StringBuilder longest, int i, int j) { while (i >= 0 && j < s.length()) { if (s.charAt(i) == s.charAt(j)) { if (j - i + 1 > longest.length()) { longest.delete(0, longest.length()); // use setLength(0) longest.append(s.substring(i, j + 1)); } i--; j++; } else break; } }
a modified version without StringBuiler - save the i, j position.
private int maxLength = 1; private int maxIndex = 0; public String longestPalindrome(String str) { //O(N^2), space O(1) int length = str.length(); for (int i=0; i<length; i++) { // find longest odd palindrome with center i findPalindrome(str, length, i, 0); // find longest even palindrome with center i findPalindrome(str, length, i, 1); } return str.substring(maxIndex, maxIndex+maxLength); } private void findPalindrome(String str, int length, int i, int shift) { int left = i; int right= i+shift; while (left >= 0 && right < length && str.charAt(left) == str.charAt(right)) { if ((right - left + 1) > maxLength) { maxLength = right - left + 1; maxIndex = left; } left--; right++; } }
http://www.programcreek.com/2013/12/leetcode-solution-of-longest-palindromic-substring-java/
X. DPTime O(n^2) Space O(n^2)
https://discuss.leetcode.com/topic/32783/clean-java-solution-using-dp-yet-the-time-complexity-is-o-n-2
https://discuss.leetcode.com/topic/25500/share-my-java-solution-using-dynamic-programming
http://blog.csdn.net/linhuanmars/article/details/20888595
dp(i, j) represents whether s(i ... j) can form a palindromic substring, dp(i, j) is true when s(i) equals to s(j) and s(i+1 ... j-1) is a palindromic substring. When we found a palindrome, check if it's the longest one. Time complexity O(n^2).
public String longestPalindrome(String s) {
int n = s.length();
String res = null;
boolean[][] dp = new boolean[n][n];
for (int i = n - 1; i >= 0; i--) {
for (int j = i; j < n; j++) {
dp[i][j] = s.charAt(i) == s.charAt(j) && (j - i < 3 || dp[i + 1][j - 1]);
if (dp[i][j] && (res == null || j - i + 1 > res.length())) {
res = s.substring(i, j + 1);
}
}
}
return res;
}
// OR save i, j, call subString at last.
A little improvement: don't substring in for j loop. Do that after for j loop finishes.
public String longestPalindrome(String s) { if(s==null || s.length() <= 1) return s; boolean[][] dp = new boolean[s.length()][s.length()]; char[] w = s.toCharArray(); int maxLen = 0; String maxSub = null; dp[s.length()-1][s.length()-1] = true; for(int i = s.length()-2;i>=0;--i){ //试每一个起点 int maxJ = i; for (int j = i+1; j < s.length(); j++) { //每一个终点 if(w[j] == w[i] && (j<i+3 || dp[i+1][j-1])){ dp[i][j] = true; maxJ = j; }else{ dp[i][j] = false; //不是立即返回. } } if(maxJ - i+1 > maxLen){ maxLen = maxJ - i+1; maxSub = s.substring(i,maxJ+1); } } return maxSub; }
substring is time-consuming
public String longestPalindrome(String s) {
if(s == null || s.length() <= 1) {
return s;
}
int len = s.length();
int start = 0, end = 0;
// palindrome[i][j] : substring(i,j) is palindrome or not?
boolean[][] palindrome = new boolean[len][len];
// length = 1
for(int i=0;i<len;i++) {
palindrome[i][i] = true;
}
// length = 2
for(int i=1;i<len;i++) {
if(s.charAt(i-1) == s.charAt(i)) {
palindrome[i-1][i] = true;
start = i-1; end = i+1;
}
}
// length = k (k=2..len)
for(int k=2;k<len;k++) {
for(int i=0;i+k<len;i++) {
int j = i+k;
if(s.charAt(i) == s.charAt(j) && palindrome[i+1][j-1]) {
palindrome[i][j] = true;
start = i; end = j+1;
}
}
}
return s.substring(start, end);
}
Let s be the input string, i and j are two indices of the string. Define a 2-dimension array "table" and let table[i][j] denote whether a substring from i to j is palindrome.
Start condition:
table[i][i] == 1; table[i][i+1] == 1 => s.charAt(i) == s.charAt(i+1)
Changing condition:
table[i+1][j-1] == 1 && s.charAt(i) == s.charAt(j) => table[i][j] == 1
public static String longestPalindrome2(String s) { if (s == null) return null; if(s.length() <=1) return s; int maxLen = 0; String longestStr = null; int length = s.length(); int[][] table = new int[length][length]; //every single letter is palindrome for (int i = 0; i < length; i++) { table[i][i] = 1; } //e.g. bcba //two consecutive same letters are palindrome for (int i = 0; i <= length - 2; i++) { if (s.charAt(i) == s.charAt(i + 1)){ table[i][i + 1] = 1; longestStr = s.substring(i, i + 2); } } //condition for calculate whole table for (int l = 3; l <= length; l++) { for (int i = 0; i <= length-l; i++) { int j = i + l - 1; if (s.charAt(i) == s.charAt(j)) { table[i][j] = table[i + 1][j - 1]; if (table[i][j] == 1 && l > maxLen) longestStr = s.substring(i, j + 1); } else { table[i][j] = 0; } } } return longestStr; }
http://blog.csdn.net/linhuanmars/article/details/20888595
而第二种方法是用动态规划,思路比较复杂一些,但是实现代码会比较简短。基本思路是外层循环i从后往前扫,内层循环j从i当前字符扫到结尾处。过程中使用的历史信息是从i+1到n之间的任意子串是否是回文已经被记录下来,所以不用重新判断,只需要比较一下头尾字符即可。这种方法使用两层循环,时间复杂度是O(n^2)。而空间上因为需要记录任意子串是否为回文,需要O(n^2)的空间,代码如下:
public String longestPalindrome(String s) {
if(s == null || s.length()==0)
return "";
boolean[][] palin = new boolean[s.length()][s.length()];
String res = "";
int maxLen = 0;
for(int i=s.length()-1;i>=0;i--)
{
for(int j=i;j<s.length();j++)
{
if(s.charAt(i)==s.charAt(j) && (j-i<=2 || palin[i+1][j-1]))
{
palin[i][j] = true;
if(maxLen<j-i+1)
{
maxLen=j-i+1;
res = s.substring(i,j+1);
}
}
}
}
return res;
}
综上所述,两种方法的时间复杂度都是O(n^2)。而空间上来看第一种方法是常量的,比第二种方法优。这个题目中假设最长回文子串只有一个,实际面试中一般不做这种假设,如果要返回所有最长回文串,只需要稍做变化就可以,维护一个集合,如果等于当前最大的,即加入集合,否则,如果更长,则清空集合,加入当前这个。实际面试会有各种变体,感觉平常还是要多想才行。
X. Manacher
http://www.geeksforgeeks.org/manachers-algorithm-linear-time-longest-palindromic-substring-part-1/
To find Longest Palindromic Substring of a string of length N, one way is take each possible 2*N + 1 centers (the N character positions, N-1 between two character positions and 2 positions at left and right ends), do the character match in both left and right directions at each 2*N+ 1 centers and keep track of LPS. This approach takes O(N^2) time
If we need to calculate Longest Palindromic Substring at each 2*N+1 positions from left to right, then palindrome’s symmetric property could help to avoid some of the unnecessary computations (i.e. character comparison). If there is a palindrome of some length L cantered at any position P, then we may not need to compare all characters in left and right side at position P+1. We already calculated LPS at positions before P and they can help to avoid some of the comparisons after position P.
http://www.geeksforgeeks.org/manachers-algorithm-linear-time-longest-palindromic-substring-part-1/
To find Longest Palindromic Substring of a string of length N, one way is take each possible 2*N + 1 centers (the N character positions, N-1 between two character positions and 2 positions at left and right ends), do the character match in both left and right directions at each 2*N+ 1 centers and keep track of LPS. This approach takes O(N^2) time
If we need to calculate Longest Palindromic Substring at each 2*N+1 positions from left to right, then palindrome’s symmetric property could help to avoid some of the unnecessary computations (i.e. character comparison). If there is a palindrome of some length L cantered at any position P, then we may not need to compare all characters in left and right side at position P+1. We already calculated LPS at positions before P and they can help to avoid some of the comparisons after position P.
public String longestPalindrome(String s) { if (s == null || s.length() == 0) { return ""; } int length = s.length(); int max = 0; String result = ""; for(int i = 1; i <= 2 * length - 1; i++){ int count = 1; while(i - count >= 0 && i + count <= 2 * length && get(s, i - count) == get(s, i + count)){ count++; } count--; // there will be one extra count for the outbound # if(count > max) { result = s.substring((i - count) / 2, (i + count) / 2); max = count; } } return result; } private char get(String s, int i) { if(i % 2 == 0) return '#'; else return s.charAt(i / 2); }
时间 O(n) 空间 O(n)
首先用一个非常巧妙的方式,将所有可能的奇数/偶数长度的回文子串都转换成了奇数长度:在每个字符的两边都插入一个特殊的符号。比如 abba 变成 #a#b#b#a#, aba变成 #a#b#a#。 为了进一步减少编码的复杂度,可以在字符串的开始加入另一个特殊字符,这样就不用特殊处理越界问题,比如$#a#b#a#(注意,下面的代码是用C语言写就,由于C语言规范还要求字符串末尾有一个'\0'所以正好OK,但其他语言可能会导致越界)。
下面以字符串12212321为例,经过上一步,变成了 S[] = "$#1#2#2#1#2#3#2#1#";
然后用一个数组 P[i] 来记录以字符S[i]为中心的最长回文子串向左/右扩张的长度(包括S[i],也就是把该回文串“对折”以后的长度),比如S和P的对应关系:
那么怎么计算P[i]呢?该算法增加两个辅助变量(其实一个就够了,两个更清晰)id和mx,其中 id 为已知的 {右边界最大} 的回文子串的中心,mx则为id+P[id],也就是这个子串的右边界。
然后可以得到一个非常神奇的结论,这个算法的关键点就在这里了:如果mx > i,那么P[i] >= MIN(P[2 * id - i], mx - i)。就是这个串卡了我非常久。实际上如果把它写得复杂一点,理解起来会简单很多:
当然光看代码还是不够清晰,还是借助图来理解比较容易。
当 mx - i > P[j] 的时候,以S[j]为中心的回文子串包含在以S[id]为中心的回文子串中,由于 i 和 j 对称,以S[i]为中心的回文子串必然包含在以S[id]为中心的回文子串中,所以必有 P[i] = P[j],见下图。
当 P[j] >= mx - i 的时候,以S[j]为中心的回文子串不一定完全包含于以S[id]为中心的回文子串中,但是基于对称性可知,下图中两个绿框所包围的部分是相同的,也就是说以S[i]为中心的回文子串,其向右至少会扩张到mx的位置,也就是说 P[i] >= mx - i。至于mx之后的部分是否对称,就只能老老实实去匹配了。
对于 mx <= i 的情况,无法对 P[i]做更多的假设,只能P[i] = 1,然后再去匹配了。
于是代码如下:
下面以字符串12212321为例,经过上一步,变成了 S[] = "$#1#2#2#1#2#3#2#1#";
然后用一个数组 P[i] 来记录以字符S[i]为中心的最长回文子串向左/右扩张的长度(包括S[i],也就是把该回文串“对折”以后的长度),比如S和P的对应关系:
S # 1 # 2 # 2 # 1 # 2 # 3 # 2 # 1 #
P 1 2 1 2 5 2 1 4 1 2 1 6 1 2 1 2 1
(p.s. 可以看出,P[i]-1正好是原字符串中回文串的总长度)
P 1 2 1 2 5 2 1 4 1 2 1 6 1 2 1 2 1
(p.s. 可以看出,P[i]-1正好是原字符串中回文串的总长度)
那么怎么计算P[i]呢?该算法增加两个辅助变量(其实一个就够了,两个更清晰)id和mx,其中 id 为已知的 {右边界最大} 的回文子串的中心,mx则为id+P[id],也就是这个子串的右边界。
然后可以得到一个非常神奇的结论,这个算法的关键点就在这里了:如果mx > i,那么P[i] >= MIN(P[2 * id - i], mx - i)。就是这个串卡了我非常久。实际上如果把它写得复杂一点,理解起来会简单很多:
//记j = 2 * id - i,也就是说 j 是 i 关于 id 的对称点(j = id + (id - i))
if (mx - i > P[j])
P[i] = P[j];
else /* P[j] >= mx - i */
P[i] = mx - i; // P[i] >= mx - i,取最小值,之后再匹配更新。
if (mx - i > P[j])
P[i] = P[j];
else /* P[j] >= mx - i */
P[i] = mx - i; // P[i] >= mx - i,取最小值,之后再匹配更新。
当然光看代码还是不够清晰,还是借助图来理解比较容易。
当 mx - i > P[j] 的时候,以S[j]为中心的回文子串包含在以S[id]为中心的回文子串中,由于 i 和 j 对称,以S[i]为中心的回文子串必然包含在以S[id]为中心的回文子串中,所以必有 P[i] = P[j],见下图。
当 P[j] >= mx - i 的时候,以S[j]为中心的回文子串不一定完全包含于以S[id]为中心的回文子串中,但是基于对称性可知,下图中两个绿框所包围的部分是相同的,也就是说以S[i]为中心的回文子串,其向右至少会扩张到mx的位置,也就是说 P[i] >= mx - i。至于mx之后的部分是否对称,就只能老老实实去匹配了。
对于 mx <= i 的情况,无法对 P[i]做更多的假设,只能P[i] = 1,然后再去匹配了。
于是代码如下:
//输入,并处理得到字符串s
int p[1000], mx = 0, id = 0;
memset(p, 0, sizeof(p));
for (i = 1; s[i] != '\0'; i++) {
p[i] = mx > i ? min(p[2*id-i], mx-i) : 1;
while (s[i + p[i]] == s[i - p[i]]) p[i]++;
if (i + p[i] > mx) {
mx = i + p[i];
id =
int p[1000], mx = 0, id = 0;
memset(p, 0, sizeof(p));
for (i = 1; s[i] != '\0'; i++) {
p[i] = mx > i ? min(p[2*id-i], mx-i) : 1;
while (s[i + p[i]] == s[i - p[i]]) p[i]++;
if (i + p[i] > mx) {
mx = i + p[i];
id =
public String longestPalindrome(String s) {
if(s.length()<=1){
return s;
}
// 预处理字符串,避免奇偶问题
String str = preProcess(s);
// idx是当前能够向右延伸的最远的回文串中心点,随着迭代而更新
// max是当前最长回文串在总字符串中所能延伸到的最右端的位置
// maxIdx是当前已知的最长回文串中心点
// maxSpan是当前已知的最长回文串向左或向右能延伸的长度
int idx = 0, max = 0;
int maxIdx = 0;
int maxSpan = 0;
int[] p = new int[str.length()];
for(int curr = 1; curr < str.length(); curr++){
// 找出当前下标相对于idx的对称点
int symmetryOfCurr = 2 * idx - curr;
// 如果当前已知延伸的最右端大于当前下标,我们可以用对称点的P值,否则记为1等待检查
p[curr] = max > curr? Math.min(p[symmetryOfCurr], max - curr):1;
// 检查并更新当前下标为中心的回文串最远延伸的长度
while((curr+p[curr])<str.length() && str.charAt(curr+p[curr])==str.charAt(curr-p[curr])){
p[curr]++;
}
// 检查并更新当前已知能够延伸最远的回文串信息
if(curr+p[curr]>max){
max = p[curr] + curr;
idx = curr;
}
// 检查并更新当前已知的最长回文串信息
if(p[curr]>maxSpan){
maxSpan = p[curr];
maxIdx = curr;
}
}
//去除占位符
return s.substring((maxIdx-maxSpan)/2,(maxSpan+maxIdx)/2-1);
}
private String preProcess(String s){
// 如ABC,变为$#A#B#C#
StringBuilder sb = new StringBuilder();
sb.append("$");
for(int i = 0; i < s.length(); i++){
sb.append("#");
sb.append(s.charAt(i));
}
sb.append("#");
return sb.toString();
}
X. Pruning
https://leetcode.com/discuss/52814/ac-relatively-short-and-very-clear-java-solution
https://discuss.leetcode.com/topic/2985/a-very-brief-o-n-time-o-1-space-solution-ac/8
https://discuss.leetcode.com/topic/35582/java-easy-understanding-solution-beats-97/4
https://discuss.leetcode.com/topic/2985/a-very-brief-o-n-time-o-1-space-solution-ac/8
https://discuss.leetcode.com/topic/35582/java-easy-understanding-solution-beats-97/4
here we could take the advantage of the property of palindrome string. Assume we check "if(isPalindrome(s,i-currLength-2,i))" as you said and get a new palindrome string, then its length should be currLength+3, right? And according to palindrome string's property, when we trim both the head and tail characters of it ,we must get a palindrome string with length = currLength+1, which means in the previous round we got longest palindrome string with length = currLength+1. This is a contradiction with our definition of currLength (It's the length of longest palindrome in previous round).
Key idea, every time we move to right, we only need to consider whether using this new character as tail could produce new palindrome string of length (current length +1) or (current length +2)
public class Solution {
public String longestPalindrome(String s) {
String res = "";
int currLength = 0;
for(int i=0;i<s.length();i++){
if(isPalindrome(s,i-currLength-1,i)){
res = s.substring(i-currLength-1,i+1);
currLength = currLength+2;
}
else if(isPalindrome(s,i-currLength,i)){
res = s.substring(i-currLength,i+1);
currLength = currLength+1;
}
}
return res;
}
public boolean isPalindrome(String s, int begin, int end){
if(begin<0) return false;
while(begin<end){
if(s.charAt(begin++)!=s.charAt(end--)) return false;
}
return true;
}
}
For friends who are confused about the key idea to check only new palindrome with length = current length +2 or +1, I add some more explanation here.
Example: "xxxbcbxxxxxa", (x is random character, not all x are equal) now we
are dealing with the last character 'a'. The current longest palindrome
is "bcb" with length 3.
1. check "xxxxa" so if it is palindrome we could get a new palindrome of length 5.
2. check "xxxa" so if it is palindrome we could get a new palindrome of length 4.
3. do NOT check "xxa" or any shorter string since the length of the new string is
no bigger than current longest length.
4. do NOT check "xxxxxa" or any longer string because if "xxxxxa" is palindrome
then "xxxx" got from cutting off the head and tail is also palindrom. It has
length > 3 which is impossible.'
X. O(N^3)
https://discuss.leetcode.com/topic/5658/optimized-n-square-solution-in-java
Naively, we can simply examine every substring and check if it is palindromic. The time complexity is O(n^3).
A:就是找到最长回文串,然后把长度减一下就行了。
https://www.geeksforgeeks.org/suffix-tree-application-6-longest-palindromic-substring/
https://www.geeksforgeeks.org/longest-palindromic-substring-set-2/
https://www.geeksforgeeks.org/suffix-tree-application-6-longest-palindromic-substring/
https://www.programering.com/a/MjNzczMwATE.html
Read full article from Longest Palindromic Substring Part I | LeetCode
https://discuss.leetcode.com/topic/5658/optimized-n-square-solution-in-java
Maybe this is a "greedy" way to find solution:
len = length of s;
Try to find a palindrome of length = len,
then length len-1, len-2, ...
Whenever we find one, this is the largest one, and we don't need to check the rest.
len = length of s;
Try to find a palindrome of length = len,
then length len-1, len-2, ...
Whenever we find one, this is the largest one, and we don't need to check the rest.
Naively, we can simply examine every substring and check if it is palindromic. The time complexity is O(n^3).
public static String longestPalindrome1(String s) { int maxPalinLength = 0; String longestPalindrome = null; int length = s.length(); // check all possible sub strings for (int i = 0; i < length; i++) { for (int j = i + 1; j < length; j++) { int len = j - i; String curr = s.substring(i, j + 1); if (isPalindrome(curr)) { if (len > maxPalinLength) { longestPalindrome = curr; maxPalinLength = len; } } } } return longestPalindrome; } public static boolean isPalindrome(String s) { for (int i = 0; i < s.length() - 1; i++) { if (s.charAt(i) != s.charAt(s.length() - 1 - i)) { return false; } } return true; }Q:如果只能在头或尾删,问最少删多少字符能使得该字符串变为回文?
A:就是找到最长回文串,然后把长度减一下就行了。
https://www.geeksforgeeks.org/suffix-tree-application-6-longest-palindromic-substring/
Method 1 ( Brute Force )
The simple approach is to check each substring whether the substring is a palindrome or not. We can run three loops, the outer two loops pick all substrings one by one by fixing the corner characters, the inner loop checks whether the picked substring is palindrome or not.
The simple approach is to check each substring whether the substring is a palindrome or not. We can run three loops, the outer two loops pick all substrings one by one by fixing the corner characters, the inner loop checks whether the picked substring is palindrome or not.
Time complexity: O ( n^3 )
Method 2 ( Dynamic Programming )
The time complexity can be reduced by storing results of subproblems. The idea is similar to this post. We maintain a boolean table[n][n] that is filled in bottom up manner. The value of table[i][j] is true, if the substring is palindrome, otherwise false. To calculate table[i][j], we first check the value of table[i+1][j-1], if the value is true and str[i] is same as str[j], then we make table[i][j] true. Otherwise, the value of table[i][j] is made false.
The time complexity can be reduced by storing results of subproblems. The idea is similar to this post. We maintain a boolean table[n][n] that is filled in bottom up manner. The value of table[i][j] is true, if the substring is palindrome, otherwise false. To calculate table[i][j], we first check the value of table[i+1][j-1], if the value is true and str[i] is same as str[j], then we make table[i][j] true. Otherwise, the value of table[i][j] is made false.
Time complexity: O ( n^2 )
Auxiliary Space: O ( n^2 )
X. ExpandAuxiliary Space: O ( n^2 )
https://www.geeksforgeeks.org/longest-palindromic-substring-set-2/
We have discussed dynamic programming solution in the previous post. The time complexity of the Dynamic Programming based solution is O(n^2) and it requires O(n^2) extra space. We can find the longest palindrome substring in (n^2) time with O(1) extra space. The idea is to generate all even length and odd length palindromes and keep track of the longest palindrome seen so far.
Step to generate odd length palindrome:
Fix a centre and expand in both directions for longer palindromes.
Fix a centre and expand in both directions for longer palindromes.
Step to generate even length palindrome
Fix two centre ( low and high ) and expand in both directions for longer palindromes.
X. Suffix TrieFix two centre ( low and high ) and expand in both directions for longer palindromes.
https://www.geeksforgeeks.org/suffix-tree-application-6-longest-palindromic-substring/
If given string is S, then approach is following:
- Reverse the string S (say reversed string is R)
- Get Longest Common Substring of S and R given that LCS in S and R must be from same position in S
Can you see why we say that LCS in R and S must be from same position in S ?
Let’s look at following examples:
- For S = xababayz and R = zyababax, LCS and LPS both are ababa (SAME)
- For S = abacdfgdcaba and R = abacdgfdcaba, LCS is abacd and LPS is aba (DIFFERENT)
- For S = pqrqpabcdfgdcba and R = abcdgfdcbapqrqp, LCS and LPS both are pqrqp (SAME)
- For S = pqqpabcdfghfdcba and R = abcdfhgfdcbapqqp, LCS is abcdf and LPS is pqqp (DIFFERENT)
We can see that LCS and LPS are not same always. When they are different ?
When S has a reversed copy of a non-palindromic substring in it which is of same or longer length than LPS in S, then LCS and LPS will be different.
In 2nd example above (S = abacdfgdcaba), for substring abacd, there exists a reverse copy dcaba in S, which is of longer length than LPS aba and so LPS and LCS are different here. Same is the scenario in 4th example.
When S has a reversed copy of a non-palindromic substring in it which is of same or longer length than LPS in S, then LCS and LPS will be different.
In 2nd example above (S = abacdfgdcaba), for substring abacd, there exists a reverse copy dcaba in S, which is of longer length than LPS aba and so LPS and LCS are different here. Same is the scenario in 4th example.
To handle this scenario we say that LPS in S is same as LCS in S and R given that LCS in R and S must be from same position in S.
If we look at 2nd example again, substring aba in R comes from exactly same position in S as substring aba in S which is ZERO (0th index) and so this is LPS.
If we look at 2nd example again, substring aba in R comes from exactly same position in S as substring aba in S which is ZERO (0th index) and so this is LPS.
The Position Constraint:


We will refer string S index as forward index (Si) and string R index as reverse index (Ri).
Based on above figure, a character with index i (forward index) in a string S of length N, will be at index N-1-i (reverse index) in it’s reversed string R.
If we take a substring of length L in string S with starting index i and ending index j (j = i+L-1), then in it’s reversed string R, the reversed substring of the same will start at index N-1-j and will end at index N-1-i.
If there is a common substring of length L at indices Si (forward index) and Ri (reverse index) in S and R, then these will come from same position in S if Ri = (N – 1) – (Si + L – 1) where N is string length.
Based on above figure, a character with index i (forward index) in a string S of length N, will be at index N-1-i (reverse index) in it’s reversed string R.
If we take a substring of length L in string S with starting index i and ending index j (j = i+L-1), then in it’s reversed string R, the reversed substring of the same will start at index N-1-j and will end at index N-1-i.
If there is a common substring of length L at indices Si (forward index) and Ri (reverse index) in S and R, then these will come from same position in S if Ri = (N – 1) – (Si + L – 1) where N is string length.
So to find LPS of string S, we find longest common string of S and R where both substrings satisfy above constraint, i.e. if substring in S is at index Si, then same substring should be in R at index (N – 1) – (Si + L – 1). If this is not the case, then this substring is not LPS candidate.
Naive [O(N*M2)] and Dynamic Programming [O(N*M)] approaches to find LCS of two strings are already discussed here which can be extended to add position constraint to give LPS of a given string.
Now we will discuss suffix tree approach which is nothing but an extension to Suffix Tree LCS approach where we will add the position constraint.
While finding LCS of two strings X and Y, we just take deepest node marked as XY (i.e. the node which has suffixes from both strings as it’s children).
While finding LPS of string S, we will again find LCS of S and R with a condition that the common substring should satisfy the position constraint (the common substring should come from same position in S). To verify position constraint, we need to know all forward and reverse indices on each internal node (i.e. the suffix indices of all leaf children below the internal nodes).
While finding LPS of string S, we will again find LCS of S and R with a condition that the common substring should satisfy the position constraint (the common substring should come from same position in S). To verify position constraint, we need to know all forward and reverse indices on each internal node (i.e. the suffix indices of all leaf children below the internal nodes).
In Generalized Suffix Tree of S#R$, a substring on the path from root to an internal node is a common substring if the internal node has suffixes from both strings S and R. The index of the common substring in S and R can be found by looking at suffix index at respective leaf node.
If string S# is of length N then:
If string S# is of length N then:
- If suffix index of a leaf is less than N, then that suffix belongs to S and same suffix index will become forward index of all ancestor nodes
- If suffix index of a leaf is greater than N, then that suffix belongs to R and reverse index for all ancestor nodes will be N – suffix index
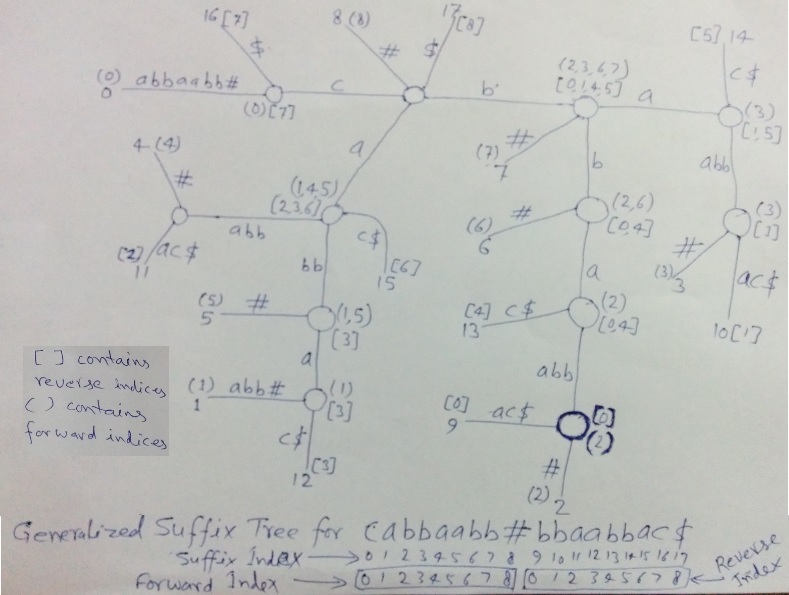
Let’s take string S = cabbaabb. The figure below is Generalized Suffix Tree for cabbaabb#bbaabbac$ where we have shown forward and reverse indices of all children suffixes on all internal nodes (except root).
Forward indices are in Parentheses () and reverse indices are in square bracket [].
Forward indices are in Parentheses () and reverse indices are in square bracket [].
https://www.programering.com/a/MjNzczMwATE.html
Read full article from Longest Palindromic Substring Part I | LeetCode