LeetCode 14 - Longest Common Prefix

https://leetcode.com/problems/longest-common-prefix/

Write a function to find the longest common prefix string amongst an array of strings.

If there is no common prefix, return an empty string "".

Example 1:

Input: ["flower","flow","flight"]
Output: "fl"

Example 2:

Input: ["dog","racecar","car"]
Output: ""
Explanation: There is no common prefix among the input strings.

Note:

All given inputs are in lowercase letters a-z

X. Trie

Given a set of keys S = $[S_1,S_2 \ldots S_n]$, find the longest common prefix among a string q and S. This LCP query will be called frequently.

We could optimize LCP queries by storing the set of keys S in a Trie. For more information about Trie, please see this article Implement a trie (Prefix trie). In a Trie, each node descending from the root represents a common prefix of some keys. But we need to find the longest common prefix of a string q and all key strings. This means that we have to find the deepest path from the root, which satisfies the following conditions: it is prefix of query string q each node along the path must contain only one child element. Otherwise the found path will not be a common prefix among all strings. * the path doesn't comprise of nodes which are marked as end of key. Otherwise the path couldn't be a prefix a of key which is shorter than itself.

In the worst case query $q$ has length $m$ and it is equal to all $n$ strings of the array.

• Time complexity : preprocessing $O(S)$, where $S$ is the number of all characters in the array, LCP query $O(m)$.
  Trie build has $O(S)$ time complexity. To find the common prefix of $q$ in the Trie takes in the worst case $O(m)$.
• Space complexity : $O(S)$. We only used additional $S$ extra space for the Trie.

public String longestCommonPrefix(String q, String[] strs) {

    if (strs == null || strs.length == 0)

        return "";

    if (strs.length == 1)

        return strs[0];

    Trie trie = new Trie();

    for (int i = 1; i < strs.length; i++) {

        trie.insert(strs[i]);

    }

    return trie.searchLongestPrefix(q);

}

class TrieNode {

    // R links to node children

    private TrieNode[] links;

    private final int R = 26;

    private boolean isEnd;

    // number of children non null links

    private int size;

    public void put(char ch, TrieNode node) {

        links[ch - 'a'] = node;

        size++;

    }

    public int getLinks() {

        return size;

    }

    // assume methods containsKey, isEnd, get, put are implemented as it is described

    // in https://leetcode.com/articles/implement-trie-prefix-tree/)

}

public class Trie {

    private TrieNode root;

    public Trie() {

        root = new TrieNode();

    }

    // assume methods insert, search, searchPrefix are implemented as it is described

    // in https://leetcode.com/articles/implement-trie-prefix-tree/)

    private String searchLongestPrefix(String word) {

        TrieNode node = root;

        StringBuilder prefix = new StringBuilder();

        for (int i = 0; i < word.length(); i++) {

            char curLetter = word.charAt(i);

            if (node.containsKey(curLetter) && (node.getLinks() == 1) && (!node.isEnd())) {

                prefix.append(curLetter);

                node = node.get(curLetter);

            } else

                return prefix.toString();

        }

        return prefix.toString();

    }

}

1. Create Trie data structure
2. Initialize with the input Strings
3. Search for longest common prefix until word is completed or there is nothing left.

    public String longestCommonPrefix(String[] strs) {
        if(strs == null || strs.length <= 0){
            return "";
        }
        Trie trie = new Trie();
        for(int i = 0; i < strs.length; i++){
            trie.insert(strs[i]);
            if(strs[i].equals("") || strs[i].length() <= 0){
                return "";
            }
        }
        
        return trie.longestPrefix();
    }

class Trie{
    TrieNode root;
    public Trie(){
        root = new TrieNode();
    }
    public Trie(String s){
        root = new TrieNode();
        root.insert(s);
    }
    
    public void insert(String s){
        root.insert(s);   
    }
    
    public String longestPrefix(){
        StringBuilder prefix = new StringBuilder();
        TrieNode node = root;
        while(node != null && node.children.keySet().size() == 1 && !node.isWord){
            Set set = node.children.keySet();
            for(Iterator itr = set.iterator();itr.hasNext();){
                node = node.children.get(itr.next());
            }
            prefix.append(node.val);
        }
        return prefix.toString();
    }
}
class TrieNode{
    char val;
    boolean isWord;
    HashMap children = new HashMap();
    
    public void insert(String s){
        if(s == null || s.length() <=0){
            isWord = true;
            return;
        }
        char curr = s.charAt(0);
        TrieNode child = null;
        if(children.containsKey(curr)){
            child = children.get(curr);
            
        }else{
            child = new TrieNode();
            child.val = curr;
            children.put(curr, child);
        }
        String remainder = s.substring(1);
        child.insert(remainder);
        
    }

X. Bisection

In the worst case we have $n$ equal strings with length $m$

• Time complexity : $O(S \cdot log(n))$, where $S$ is the sum of all characters in all strings.
  The algorithm makes $log(n)$ iterations, for each of them there are $S = m*n$ comparisons, which gives in total $O(S \cdot log(n))$ time complexity.
• Space complexity : $O(1)$. We only used constant extra space. 

public String longestCommonPrefix(String[] strs) {

    if (strs == null || strs.length == 0)

        return "";

    int minLen = Integer.MAX_VALUE;

    for (String str : strs)

        minLen = Math.min(minLen, str.length());

    int low = 1;

    int high = minLen;

    while (low <= high) {

        int middle = (low + high) / 2;

        if (isCommonPrefix(strs, middle))

            low = middle + 1;

        else

            high = middle - 1;

    }

    return strs[0].substring(0, (low + high) / 2);

}

private boolean isCommonPrefix(String[] strs, int len) {

    String str1 = strs[0].substring(0, len);

    for (int i = 1; i < strs.length; i++)

        if (!strs[i].startsWith(str1))

            return false;

    return true;

}

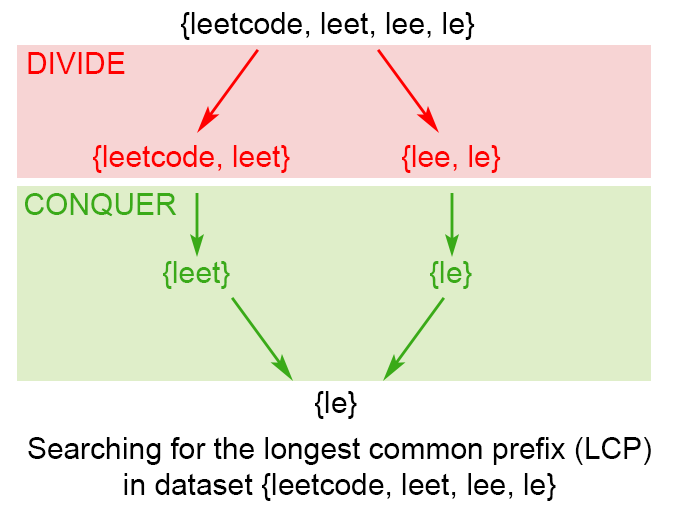
X. Divide and conquer

In the worst case we have $n$ equal strings with length $m$

• Time complexity : $O(S)$, where $S$ is the number of all characters in the array, $S = m*n$ Time complexity is $2 \cdot T\left ( \frac{n}{2} \right ) + O(m)$. Therefore time complexity is $O(S)$. In the best case this algorithm performs $O(minLen \cdot n)$ comparisons, where $minLen$ is the shortest string of the array
• Space complexity : $O(m \cdot log(n))$
  There is a memory overhead since we store recursive calls in the execution stack. There are $log(n)$recursive calls, each store need $m$ space to store the result, so space complexity is $O(m \cdot log(n))$

public String longestCommonPrefix(String[] strs) {

    if (strs == null || strs.length == 0)

        return "";

    return longestCommonPrefix(strs, 0, strs.length - 1);

}

private String longestCommonPrefix(String[] strs, int l, int r) {

    if (l == r) {

        return strs[l];

    } else {

        int mid = (l + r) / 2;

        String lcpLeft = longestCommonPrefix(strs, l, mid);

        String lcpRight = longestCommonPrefix(strs, mid + 1, r);

        return commonPrefix(lcpLeft, lcpRight);

    }

}

String commonPrefix(String left, String right) {

    int min = Math.min(left.length(), right.length());

    for (int i = 0; i < min; i++) {

        if (left.charAt(i) != right.charAt(i))

            return left.substring(0, i);

    }

    return left.substring(0, min);

}

http://www.programcreek.com/2014/02/leetcode-longest-common-prefix-java/

To solve this problem, we need to find the two loop conditions. One is the length of the shortest string. The other is iteration over every element of the string array.

public String longestCommonPrefix(String[] strs) { if(strs == null || strs.length == 0) return "";   int minLen=Integer.MAX_VALUE; for(String str: strs){ if(minLen > str.length()) minLen = str.length(); } if(minLen == 0) return "";   for(int j=0; j<minLen; j++){ char prev='0'; for(int i=0; i<strs.length ;i++){ if(i==0) { prev = strs[i].charAt(j); continue; }   if(strs[i].charAt(j) != prev){ return strs[i].substring(0, j); } } }   return strs[0].substring(0,minLen); }

http://www.jiuzhang.com/solutions/longest-common-prefix/

    // 1. Method 1, start from the first one, compare prefix with next string, until end;
    // 2. Method 2, start from the first char, compare it with all string, and then the second char
    // I am using method 1 here
    public String longestCommonPrefix(String[] strs) {
        if (strs == null || strs.length == 0) {
            return "";
        }
        String prefix = strs[0];
        for(int i = 1; i < strs.length; i++) {
            int j = 0;
            while( j < strs[i].length() && j < prefix.length() && strs[i].charAt(j) == prefix.charAt(j)) {
                j++;
            }
            if( j == 0) {
                return "";
     }
            prefix = prefix.substring(0, j);
        }
        return prefix;
    }

https://leetcode.com/discuss/32176/fast-and-simple-java-code-231ms
public String longestCommonPrefix(List<String> strs) { if(strs.size()==0) return ""; StringBuilder lcp=new StringBuilder(); for(int i=0;i<strs.get(0).length();i++){ char c=strs.get(0).charAt(i); for(String s:strs){ if(s.length()<i+1||c!=s.charAt(i)) return lcp.toString();//\\ } lcp.append(c); } return lcp.toString(); }

Rather than building the string for common prefix, you can just record the longest prefix's length, then return the substring from first character till that length, which can save a bit time perhaps.

var longestCommonPrefix = function(strs) {
    if (strs.length === 0) return "";
    if (strs.length === 1) return strs[0];

    for (var i = 0; i < strs[0].length; i++) {
        for (var j = 1; j < strs.length; j++) {
            if (strs[j].length <= i || strs[j][i] !== strs[0][i]) {
                return strs[0].substring(0, i);
            }
        }
    }
    return strs[0];
};

https://leetcode.com/discuss/89652/my-2ms-java-solution-may-help-u
doesn't really help to get the min len
public String longestCommonPrefix(String[] strs) { int len = strs.length; if (len == 0) return ""; int minlen = 0x7fffffff; for (int i = 0; i < len; ++i) minlen = Math.min(minlen, strs[i].length());//\\ for (int j = 0; j < minlen; ++j) for (int i = 1; i < len; ++i) if (strs[0].charAt(j) != strs[i].charAt(j)) return strs[0].substring(0, j); return strs[0].substring(0, minlen); }
Don't use trie.
http://comproguide.blogspot.com/2014/05/finding-longest-common-prefix-from.html

string longestCommonPrefix(vector<string> & strVect)


{


string result;




if( strVect.size() > 0 ) //proceed only if not empty


result = strVect[0]; //Assume first string as longest common prefix


int i,j;


//in each iteration try to match the whole prefix; if not matching reduce it


for( i = 1; i < strVect.size(); i++ )


{


int m = min( result.size(), strVect[i].size() );


for( j = 0; j < m; j++ )


{


if( result[j] != strVect[i][j] )


break;


}


result = result.substr(0,j);


//this condition will prevent further checking of the prefix is already empty


if( result.empty() )


break;


}


return result;


}

X. Sort
https://leetcode.com/problems/longest-common-prefix/discuss/6924/Sorted-the-array-Java-solution-2-ms

Sort the array first, and then you can simply compare the first and last elements in the sorted array.

Not a good solution, there's no need to sort the entire array since you're only using the min and max values. You can just find the min and max directly in a single pass of the array.

Stylistically, the else statement within the for is unnecessary if you just move your if check into the for loop check. You also don't need a StringBuilder, all you need is the value of i then call min.substring using it

    public String longestCommonPrefix(String[] strs) {
        StringBuilder result = new StringBuilder();

        if (strs!= null && strs.length > 0){

            Arrays.sort(strs);

            char [] a = strs[0].toCharArray();
            char [] b = strs[strs.length-1].toCharArray();

            for (int i = 0; i < a.length; i ++){
                if (b.length > i && b[i] == a[i]){
                    result.append(b[i]);
                }
                else {
                    return result.toString();
                }
            }
        return result.toString();
    }

Nice but you don't have to sort the array to get the first and last string in the sorted array. It will cost O(n log n).

Also, we can use .charAt() to get the specific character in the string, it also cost O(1). Therefore, we don't have to create an extra char array.

    public String longestCommonPrefix(String[] strs) {
        if (strs == null)       return null;
        if (strs.length == 0)   return "";
        
        String first = strs[0], last = strs[0];
        
        for (String str : strs) {
            if (str.compareTo(first) < 0)
                first = str;
            if (str.compareTo(last) > 0)
                last = str;
        }
        
        int i = 0, len = Math.min(first.length(), last.length());
        
        while (i < len && first.charAt(i) == last.charAt(i))
            i++;
        
        return first.substring(0, i);




X.
Approach 1: Horizontal scanning
https://leetcode.com/articles/longest-common-prefix/

• Time complexity : $O(S)$ , where S is the sum of all characters in all strings.
  In the worst case all $n$ strings are the same. The algorithm compares the string $S1$ with the other strings $[S_2 \ldots S_n]$ There are $S$ character comparisons, where $S$ is the sum of all characters in the input array.

public String longestCommonPrefix(String[] strs) {

    if (strs.length == 0)

        return "";

    String prefix = strs[0];

    for (int i = 1; i < strs.length; i++)

        while (strs[i].indexOf(prefix) != 0) {

            prefix = prefix.substring(0, prefix.length() - 1);

            if (prefix.isEmpty())

                return "";

        }

    return prefix;

}

Approach 2: Vertical scanning

Imagine a very short string is at the end of the array. The above approach will still do $S$ comparisons. One way to optimize this case is to do vertical scanning. We compare characters from top to bottom on the same column (same character index of the strings) before moving on to the next column.

• Time complexity : $O(S)$ , where S is the sum of all characters in all strings. In the worst case there will be $n$ equal strings with length $m$ and the algorithm performs $S = m*n$ character comparisons. Even though the worst case is still the same as Approach 1, in the best case there are at most $n*minLen$ comparisons where $minLen$ is the length of the shortest string in the array.

public String longestCommonPrefix(String[] strs) {

    if (strs == null || strs.length == 0)

        return "";

    for (int i = 0; i < strs[0].length(); i++) {

        char c = strs[0].charAt(i);

        for (int j = 1; j < strs.length; j++) {

            if (i == strs[j].length() || strs[j].charAt(i) != c)

                return strs[0].substring(0, i);

        }

    }

    return strs[0];

}

Also read http://fisherlei.blogspot.com/2012/12/leetcode-longest-common-prefix.html
Read full article from LeetCode: Longest Common Prefix in Java | Param's Blog