LeetCode 56 - Merge Intervals


LeetCode – Merge Intervals
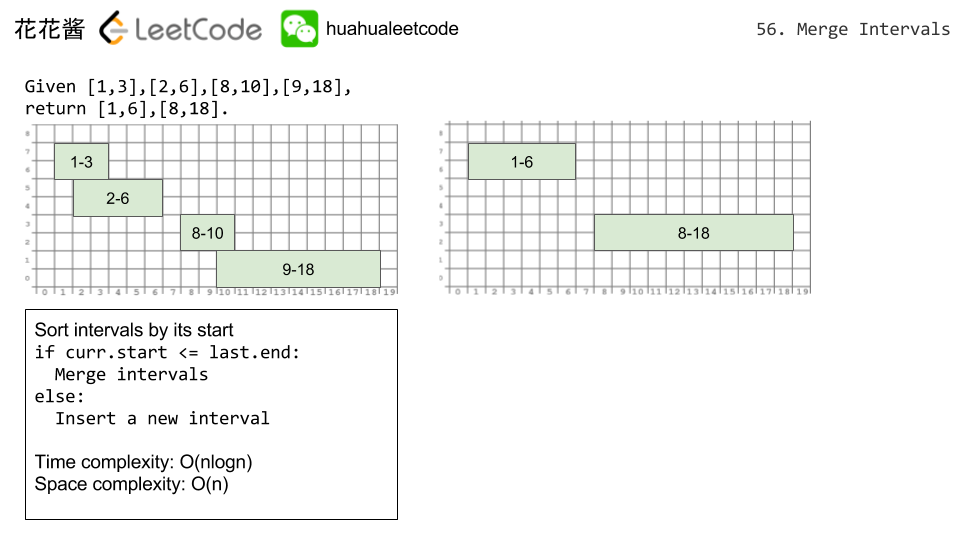
Given a collection of intervals, merge all overlapping intervals.
For example,
Given [1,3],[2,6],[8,10],[15,18],
return [1,6],[8,10],[15,18].









  private class IntervalComparator implements Comparator<Interval> {
    @Override
    public int compare(Interval a, Interval b) {
      return a.start < b.start ? -1 : a.start == b.start ? 0 : 1;
    }
  }

  public List<Interval> merge(List<Interval> intervals) {
    Collections.sort(intervals, new IntervalComparator());

    LinkedList<Interval> merged = new LinkedList<Interval>();
    for (Interval interval : intervals) {
      // if the list of merged intervals is empty or if the current
      // interval does not overlap with the previous, simply append it.
      if (merged.isEmpty() || merged.getLast().end < interval.start) {
        merged.add(interval);
      }
      // otherwise, there is overlap, so we merge the current and previous
      // intervals.
      else {
        merged.getLast().end = Math.max(merged.getLast().end, interval.end);
      }
    }

    return merged;
  }



First sort the intervals according to starting time. Once we have the sorted intervals, we can combine all intervals in a linear traversal. The idea is, in sorted array of intervals, if interval[i] doesn’t overlap with interval[i-1], then interval[i+1] cannot overlap with interval[i-1] because starting time of interval[i+1] must be greater than or equal to interval[i]. 

 1. Sort the intervals based on increasing order of starting time.
2. Push the first interval on to a stack.
3. For each interval do the following
……..a. If the current interval does not overlap with the stack top, push it.
……..b. If the current interval overlaps with stack top and ending time of current interval is more than that of stack top, update stack top with the ending time of current interval.
4. At the end stack contains the merged intervals.

 The key to solve this problem is defining a Comparator first to sort the arraylist of Intevals. And then merge some intervals.
The take-away message from this problem is utilizing the advantage of sorted list/array.
 public ArrayList<Interval> merge(ArrayList<Interval> intervals) {
 
  if (intervals == null || intervals.size() <= 1)
   return intervals;
 
  // sort intervals by using self-defined Comparator
  Collections.sort(intervals, new IntervalComparator());
 
  ArrayList<Interval> result = new ArrayList<Interval>();
 
  Interval prev = intervals.get(0);
  for (int i = 1; i < intervals.size(); i++) {
   Interval curr = intervals.get(i);
 
   if (prev.end >= curr.start) {
    // merged case
    Interval merged = new Interval(prev.start, Math.max(prev.end, curr.end));
    prev = merged; // this is better, another way is always compare with latest from list, merge and update it.
   } else {
    result.add(prev);
    prev = curr;
   }
  }
 
  result.add(prev);
 
  return result;
 }
class IntervalComparator implements Comparator<Interval> {
 public int compare(Interval i1, Interval i2) {
  return i1.start - i2.start;
 }
}

The key to solve this problem is defining a Comparator first to sort the arraylist of Intevals. And then merge some intervals.
The take-away message from this problem is utilizing the advantage of sorted list/array.
http://blog.csdn.net/linhuanmars/article/details/21857617
http://happycoding2010.blogspot.com/2015/09/leetcode-55-merge-intervals.html
public ArrayList<Interval> merge(ArrayList<Interval> intervals) {
    ArrayList<Interval> res = new ArrayList<Interval>();
    if(intervals==null || intervals.size()==0)
        return intervals;
    Comparator<Interval> comp = new Comparator<Interval>()
    {
        @Override
        public int compare(Interval i1, Interval i2)
        {
            if(i1.start==i2.start)
                return i1.end-i2.end;
            return i1.start-i2.start;
        }
    };
    Collections.sort(intervals,comp);
    
    res.add(intervals.get(0));
    for(int i=1;i<intervals.size();i++)
    {
        if(res.get(res.size()-1).end>=intervals.get(i).start)
        {
            res.get(res.size()-1).end = Math.max(res.get(res.size()-1).end, intervals.get(i).end);
        }
        else
        {
            res.add(intervals.get(i));
        }
    }
    return res;
}
https://leetcode.com/articles/merge-intervals/
  private class IntervalComparator implements Comparator<Interval> {
    @Override
    public int compare(Interval a, Interval b) {
      return a.start < b.start ? -1 : a.start == b.start ? 0 : 1;
    }
  }

  public List<Interval> merge(List<Interval> intervals) {
    Collections.sort(intervals, new IntervalComparator());

    LinkedList<Interval> merged = new LinkedList<Interval>();
    for (Interval interval : intervals) {
      // if the list of merged intervals is empty or if the current
      // interval does not overlap with the previous, simply append it.
      if (merged.isEmpty() || merged.getLast().end < interval.start) {
        merged.add(interval);
      }
      // otherwise, there is overlap, so we merge the current and previous
      // intervals.
      else {
        merged.getLast().end = Math.max(merged.getLast().end, interval.end);
      }
    }

    return merged;

  }
https://discuss.leetcode.com/topic/4319/a-simple-java-solution
The idea is to sort the intervals by their starting points. Then, we take the first interval and compare its end with the next intervals starts. As long as they overlap, we update the end to be the max end of the overlapping intervals. Once we find a non overlapping interval, we can add the previous "extended" interval and start over.
Sorting takes O(n log(n)) and merging the intervals takes O(n). So, the resulting algorithm takes O(n log(n)).
public List<Interval> merge(List<Interval> intervals) {
    if (intervals.size() <= 1)
        return intervals;
    
    // Sort by ascending starting point using an anonymous Comparator
    Collections.sort(intervals, new Comparator<Interval>() {
        @Override
        public int compare(Interval i1, Interval i2) {
            return Integer.compare(i1.start, i2.start);
        }
    });
    
    List<Interval> result = new LinkedList<Interval>();
    int start = intervals.get(0).start;
    int end = intervals.get(0).end;
    
    for (Interval interval : intervals) {
        if (interval.start <= end) // Overlapping intervals, move the end if needed
            end = Math.max(end, interval.end);
        else {                     // Disjoint intervals, add the previous one and reset bounds
            result.add(new Interval(start, end));
            start = interval.start;
            end = interval.end;
        }
    }
    
    // Add the last interval
    result.add(new Interval(start, end));
    return result;
}
https://discuss.leetcode.com/topic/12788/a-clean-java-solution/4
    public List<Interval> merge(List<Interval> intervals) {
        Collections.sort(intervals, new Comparator<Interval>(){
            @Override
            public int compare(Interval obj0, Interval obj1) {
                return obj0.start - obj1.start;
            }
        });

        List<Interval> ret = new ArrayList<>();
        Interval prev = null;
        for (Interval inter : intervals) {
            if (  prev==null || inter.start>prev.end ) {
                ret.add(inter);
                prev = inter;
            } else if (inter.end>prev.end) {
                // Modify the element already in list
                prev.end = inter.end;
            }
        }
        return ret;
    }
https://leetcode.com/discuss/33434/a-clean-java-solution
public List<Interval> merge(List<Interval> intervals) { Collections.sort(intervals, new Comparator<Interval>(){ @Override public int compare(Interval obj0, Interval obj1) { return obj0.start - obj1.start; } }); List<Interval> ret = new ArrayList<>(); Interval prev = null; for (Interval inter : intervals) { if ( prev==null || inter.start>prev.end ) { ret.add(inter); prev = inter; } else if (inter.end>prev.end) { // Modify the element already in list prev.end = inter.end; } } return ret; }
https://leetcode.com/discuss/24664/fast-ana-simple-java-code
public List<Interval> merge(List<Interval> intervals) { List<Interval> res = new LinkedList<Interval>(); if(intervals.size()<2) return intervals; Collections.sort(intervals, new Comparator<Interval>() { @Override public int compare(Interval o1, Interval o2) { return o1.start-o2.start; } }); Interval curr = intervals.get(0); for(Interval iter: intervals) { if(curr.end >= iter.start) { curr.end = Math.max(curr.end,iter.end); }else { res.add(curr); curr = iter; } } res.add(curr); return res; }

X. https://leetcode.com/discuss/78968/14ms-java-in-place-merge-solution
public List<Interval> merge(List<Interval> intervals) { int N = intervals.size(); Collections.sort(intervals, new Comparator<Interval>(){ public int compare(Interval i, Interval j){ return i.end - j.end; } }); for(int i = N-1; i>0;i--){ Interval inter1 = intervals.get(i-1); Interval inter2 = intervals.get(i); if(inter1.end >= inter2.start){ inter1.start = Math.min(inter1.start, inter2.start); inter1.end = inter2.end; //inter1.end is always smaller than inter2.end because of the sort, so no need to use Math.max() intervals.remove(i); } } return intervals; }

X. https://discuss.leetcode.com/topic/38628/beat-98-java-sort-start-end-respectively
The idea is that for the result distinct Interval, the latter one's start must > previous one's end.
public List<Interval> merge(List<Interval> intervals) {
 // sort start&end
 int n = intervals.size();
 int[] starts = new int[n];
 int[] ends = new int[n];
 for (int i = 0; i < n; i++) {
  starts[i] = intervals.get(i).start;
  ends[i] = intervals.get(i).end;
 }
 Arrays.sort(starts);
 Arrays.sort(ends);
 // loop through
 List<Interval> res = new ArrayList<Interval>();
 for (int i = 0, j = 0; i < n; i++) { // j is start of interval.
  if (i == n - 1 || starts[i + 1] > ends[i]) {
   res.add(new Interval(starts[j], ends[i]));
   j = i + 1;
  }
 }
 return res;
}

http://www.geeksforgeeks.org/merging-intervals/
Merge intervals in place:
void mergeIntervals(Interval arr[], int n)
{
    // Sort Intervals in decreasing order of
    // start time
    sort(arr, arr+n, mycomp);
    int index = 0; // Stores index of last element
                   // in output array (modified arr[])
    // Traverse all input Intervals
    for (int i=0; i<n; i++)
    {
        // If this is not first Interval and overlaps
        // with the previous one
        if (index != 0 && arr[index-1].s <= arr[i].e)
        {
            // Merge previous and current Intervals
            arr[index-1].e = max(arr[index-1].e, arr[i].e);
            arr[index-1].s = min(arr[index-1].s, arr[i].s);
        }
        else  // Doesn't overlap with previous, add to
        {     // solution
            arr[index] = arr[i];
            index++;
        }
    }
    // Now arr[0..index-1] stores the merged Intervals
    cout << "\n The Merged Intervals are: ";
    for (int i = 0; i < index; i++)
        cout << "[" << arr[i].s << ", " << arr[i].e << "] ";
}

void mergeIntervals(vector<Interval>& intervals)
{
    // Test if the given set has at least one interval
    if (intervals.size() <= 0)
        return;
    // Create an empty stack of intervals
    stack<Interval> s;
    // sort the intervals based on start time
    sort(intervals.begin(), intervals.end(), compareInterval);
    // push the first interval to stack
    s.push(intervals[0]);
    // Start from the next interval and merge if necessary
    for (int i = 1 ; i < intervals.size(); i++)
    {
        // get interval from stack top
        Interval top = s.top();
        // if current interval is not overlapping with stack top,
        // push it to the stack
        if (top.end < intervals[i].start)
        {
            s.push( intervals[i] );
        }
        // Otherwise update the ending time of top if ending of current
        // interval is more
        else if (top.end < intervals[i].end)
        {
            top.end = intervals[i].end;
            s.pop();
            s.push(top);
        }
    }
    // Print contents of stack
    cout << "\n The Merged Intervals are: ";
    while (!s.empty())
    {
        Interval t = s.top();
        cout << "[" << t.start << "," << t.end << "]" << " ";
        s.pop();
    }
    return;
}
http://www.lifeincode.net/programming/leetcode-merge-intervals-java/
    public List<Interval> merge(List<Interval> intervals) {
        List<Interval> ret = new LinkedList<>();
        if (intervals.size() == 0)
            return ret;
        Collections.sort(intervals, new Comparator<Interval>() {
            @Override
            public int compare(Interval o1, Interval o2) {
                if (o1.start > o2.start)
                    return 1;
                else if (o1.start < o2.start)
                    return -1;
                else {
                    if (o1.end > o2.end)
                        return 1;
                    else if (o1.end < o2.end)
                        return -1;
                }
                return 0;
            }
        });
        
        Interval t = null; // it would be better if we read from 1.
        for (Interval interval : intervals) {
            if (t == null)
                t = interval;
            else {
                if (t.end >= interval.start) {
                    t.end = Math.max(t.end, interval.end);
                } else {
                    ret.add(t);
                    t = interval;
                }
            }
        }
        ret.add(t);
        return ret;
    }
https://leetcode.com/articles/merge-intervals/
Approach 1: Connected Components
  • Time complexity : O(n^2)
    Building the graph costs O(V + E) = O(V) + O(E) = O(n) + O(n^2) = O(n^2) time, as in the worst case all intervals are mutually overlapping. Traversing the graph has the same cost (although it might appear higher at first) because our visited set guarantees that each node will be visited exactly once. Finally, because each node is part of exactly one component, the merge step costs O(V) = O(n) time. This all adds up as follows:
    O(n^2) + O(n^2) + O(n) = O(n^2)
  • Space complexity : O(n^2)
    As previously mentioned, in the worst case, all intervals are mutually overlapping, so there will be an edge for every pair of intervals. Therefore, the memory footprint is quadratic in the input size.
  private Map<Interval, List<Interval>> graph;
  private Map<Integer, List<Interval>> nodesInComp;
  private Set<Interval> visited;

  // return whether two intervals overlap (inclusive)
  private boolean overlap(Interval a, Interval b) {
    return a.start <= b.end && b.start <= a.end;
  }

  // build a graph where an undirected edge between intervals u and v exists
  // iff u and v overlap.
  private void buildGraph(List<Interval> intervals) {
    graph = new HashMap<>();
    for (Interval interval : intervals) {
      graph.put(interval, new LinkedList<>());
    }

    for (Interval interval1 : intervals) {
      for (Interval interval2 : intervals) {
        if (overlap(interval1, interval2)) {
          graph.get(interval1).add(interval2);
          graph.get(interval2).add(interval1);
        }
      }
    }
  }

  // merges all of the nodes in this connected component into one interval.
  private Interval mergeNodes(List<Interval> nodes) {
    int minStart = nodes.get(0).start;
    for (Interval node : nodes) {
      minStart = Math.min(minStart, node.start);
    }

    int maxEnd = nodes.get(0).end;
    for (Interval node : nodes) {
      maxEnd = Math.max(maxEnd, node.end);
    }

    return new Interval(minStart, maxEnd);
  }

  // use depth-first search to mark all nodes in the same connected component
  // with the same integer.
  private void markComponentDFS(Interval start, int compNumber) {
    Stack<Interval> stack = new Stack<>();
    stack.add(start);

    while (!stack.isEmpty()) {
      Interval node = stack.pop();
      if (!visited.contains(node)) {
        visited.add(node);

        if (nodesInComp.get(compNumber) == null) {
          nodesInComp.put(compNumber, new LinkedList<>());
        }
        nodesInComp.get(compNumber).add(node);

        for (Interval child : graph.get(node)) {
          stack.add(child);
        }
      }
    }
  }

  // gets the connected components of the interval overlap graph.
  private void buildComponents(List<Interval> intervals) {
    nodesInComp = new HashMap();
    visited = new HashSet();
    int compNumber = 0;

    for (Interval interval : intervals) {
      if (!visited.contains(interval)) {
        markComponentDFS(interval, compNumber);
        compNumber++;
      }
    }
  }

  public List<Interval> merge(List<Interval> intervals) {
    buildGraph(intervals);
    buildComponents(intervals);

    // for each component, merge all intervals into one interval.
    List<Interval> merged = new LinkedList<>();
    for (int comp = 0; comp < nodesInComp.size(); comp++) {
      merged.add(mergeNodes(nodesInComp.get(comp)));
    }

    return merged;

  }

https://github.com/mintycc/OnlineJudge-Solutions/blob/master/Leetcode/056_Merge_Intervals.java
Follow up:
1. followup是如果有⼀一个⾮非常⻓长怎么办
2. 变种:given two sorted arrays of intervals, return the intersection.
ex. a = [(1 5), (8, 10), (15 20)] sorted b = [(2 6), (45 100)] sorted return
[(2, 5)] 我⽤用了了两个pointer指着a和b然后⽤用了了⼏几个case对⽐比 follow up:如何
improve？举了了说很像merge 2 sorted array的问题，说可以⽤用类似⽅方法 然
后就解释了了⼀一⻓长⼀一短两个array的时候可以⽤用遍历短array元素，同时⽤用
binary search 查询⻓长array元素。时间是O(SlogL)的
3. 跟原题不不⼀一样的是他给了了我两个list of intervals 这两个list⾥里里⾯面的
interval都已经各⾃自按照start time sorted了
https://github.com/mintycc/OnlineJudge-Solutions/blob/master/untag/Merge%20Two%20Sorted%20Arrays%20of%20Intervals/MergeTwoSortedArraysIntervals.java
2. Two arrays of Intervals merge/intersect
    public List<Interval> merge(List<Interval> a, List<Interval> b) {
        int i = 0, j = 0;
        Interval last = null;
        List<Interval> ans = new ArrayList<>();
        while (i < a.size() || j < b.size()) {
            // pick the one with less start
            Interval cur = null;
            if (j == b.size()  || (i < a.size() && a.get(i).start < b.get(j).start)) 
                cur = a.get(i ++);
            else cur = b.get(j ++);

            // merge intervals
            if (last == null) {last = cur; continue;}
            if (last.end < cur.start) {
                ans.add(last);
                last = cur;
            } else last.end = Math.max(last.end, cur.end);
        }
        if (last != null) ans.add(last);
        return ans;
    }

    public List<Interval> intersect(List<Interval> a, List<Interval> b) {
        int i = 0, j = 0;
        List<Interval> ans = new ArrayList<>();
        while (i < a.size() && j < b.size()) {

            Interval cura = a.get(i);
            Interval curb = b.get(j);
            if (!(cura.end < curb.start || curb.end < cura.start)) {
                Interval inter = new Interval(Math.max(cura.start, curb.start), 
                    Math.min(cura.end, curb.end));
                ans.add(inter);
            }

            if (cura.end < curb.end) i ++;
            else j ++;
        }
        return ans;
    }



at
Labels: , , , , , , ,

Labels

LeetCode (1432) GeeksforGeeks (1122) LeetCode - Review (1067) Review (882) Algorithm (668) to-do (609) Classic Algorithm (270) Google Interview (237) Classic Interview (222) Dynamic Programming (220) DP (186) Bit Algorithms (145) POJ (141) Math (137) Tree (132) LeetCode - Phone (129) EPI (122) Cracking Coding Interview (119) DFS (115) Difficult Algorithm (115) Lintcode (115) Different Solutions (110) Smart Algorithm (104) Binary Search (96) BFS (91) HackerRank (90) Binary Tree (86) Hard (79) Two Pointers (78) Stack (76) Company-Facebook (75) BST (72) Graph Algorithm (72) Time Complexity (69) Greedy Algorithm (68) Interval (63) Company - Google (62) Geometry Algorithm (61) Interview Corner (61) LeetCode - Extended (61) Union-Find (60) Trie (58) Advanced Data Structure (56) List (56) Priority Queue (53) Codility (52) ComProGuide (50) LeetCode Hard (50) Matrix (50) Bisection (48) Segment Tree (48) Sliding Window (48) USACO (46) Space Optimization (45) Company-Airbnb (41) Greedy (41) Mathematical Algorithm (41) Tree - Post-Order (41) ACM-ICPC (40) Algorithm Interview (40) Data Structure Design (40) Graph (40) Backtracking (39) Data Structure (39) Jobdu (39) Random (39) Codeforces (38) Knapsack (38) LeetCode - DP (38) Recursive Algorithm (38) String Algorithm (38) TopCoder (38) Sort (37) Introduction to Algorithms (36) Pre-Sort (36) Beauty of Programming (35) Must Known (34) Binary Search Tree (33) Follow Up (33) prismoskills (33) Palindrome (32) Permutation (31) Array (30) Google Code Jam (30) HDU (30) Array O(N) (29) Logic Thinking (29) Monotonic Stack (29) Puzzles (29) Code - Detail (27) Company-Zenefits (27) Microsoft 100 - July (27) Queue (27) Binary Indexed Trees (26) TreeMap (26) to-do-must (26) 1point3acres (25) GeeksQuiz (25) Merge Sort (25) Reverse Thinking (25) hihocoder (25) Company - LinkedIn (24) Hash (24) High Frequency (24) Summary (24) Divide and Conquer (23) Proof (23) Game Theory (22) Topological Sort (22) Lintcode - Review (21) Tree - Modification (21) Algorithm Game (20) CareerCup (20) Company - Twitter (20) DFS + Review (20) DP - Relation (20) Brain Teaser (19) DP - Tree (19) Left and Right Array (19) O(N) (19) Sweep Line (19) UVA (19) DP - Bit Masking (18) LeetCode - Thinking (18) KMP (17) LeetCode - TODO (17) Probabilities (17) Simulation (17) String Search (17) Codercareer (16) Company-Uber (16) Iterator (16) Number (16) O(1) Space (16) Shortest Path (16) itint5 (16) DFS+Cache (15) Dijkstra (15) Euclidean GCD (15) Heap (15) LeetCode - Hard (15) Majority (15) Number Theory (15) Rolling Hash (15) Tree Traversal (15) Brute Force (14) Bucket Sort (14) DP - Knapsack (14) DP - Probability (14) Difficult (14) Fast Power Algorithm (14) Pattern (14) Prefix Sum (14) TreeSet (14) Algorithm Videos (13) Amazon Interview (13) Basic Algorithm (13) Codechef (13) Combination (13) Computational Geometry (13) DP - Digit (13) LCA (13) LeetCode - DFS (13) Linked List (13) Long Increasing Sequence(LIS) (13) Math-Divisible (13) Reservoir Sampling (13) mitbbs (13) Algorithm - How To (12) Company - Microsoft (12) DP - Interval (12) DP - Multiple Relation (12) DP - Relation Optimization (12) LeetCode - Classic (12) Level Order Traversal (12) Prime (12) Pruning (12) Reconstruct Tree (12) Thinking (12) X Sum (12) AOJ (11) Bit Mask (11) Company-Snapchat (11) DP - Space Optimization (11) Dequeue (11) Graph DFS (11) MinMax (11) Miscs (11) Princeton (11) Quick Sort (11) Stack - Tree (11) 尺取法 (11) 挑战程序设计竞赛 (11) Coin Change (10) DFS+Backtracking (10) Facebook Hacker Cup (10) Fast Slow Pointers (10) HackerRank Easy (10) Interval Tree (10) Limited Range (10) Matrix - Traverse (10) Monotone Queue (10) SPOJ (10) Starting Point (10) States (10) Stock (10) Theory (10) Tutorialhorizon (10) Kadane - Extended (9) Mathblog (9) Max-Min Flow (9) Maze (9) Median (9) O(32N) (9) Quick Select (9) Stack Overflow (9) System Design (9) Tree - Conversion (9) Use XOR (9) Book Notes (8) Company-Amazon (8) DFS+BFS (8) DP - States (8) Expression (8) Longest Common Subsequence(LCS) (8) One Pass (8) Quadtrees (8) Traversal Once (8) Trie - Suffix (8) 穷竭搜索 (8) Algorithm Problem List (7) All Sub (7) Catalan Number (7) Cycle (7) DP - Cases (7) Facebook Interview (7) Fibonacci Numbers (7) Flood fill (7) Game Nim (7) Graph BFS (7) HackerRank Difficult (7) Hackerearth (7) Inversion (7) Kadane’s Algorithm (7) Manacher (7) Morris Traversal (7) Multiple Data Structures (7) Normalized Key (7) O(XN) (7) Radix Sort (7) Recursion (7) Sampling (7) Suffix Array (7) Tech-Queries (7) Tree - Serialization (7) Tree DP (7) Trie - Bit (7) 蓝桥杯 (7) Algorithm - Brain Teaser (6) BFS - Priority Queue (6) BFS - Unusual (6) Classic Data Structure Impl (6) DP - 2D (6) DP - Monotone Queue (6) DP - Unusual (6) DP-Space Optimization (6) Dutch Flag (6) How To (6) Interviewstreet (6) Knapsack - MultiplePack (6) Local MinMax (6) MST (6) Minimum Spanning Tree (6) Number - Reach (6) Parentheses (6) Pre-Sum (6) Probability (6) Programming Pearls (6) Rabin-Karp (6) Reverse (6) Scan from right (6) Schedule (6) Stream (6) Subset Sum (6) TSP (6) Xpost (6) n00tc0d3r (6) reddit (6) AI (5) Abbreviation (5) Anagram (5) Art Of Programming-July (5) Assumption (5) Bellman Ford (5) Big Data (5) Code - Solid (5) Code Kata (5) Codility-lessons (5) Coding (5) Company - WMware (5) Convex Hull (5) Crazyforcode (5) DFS - Multiple (5) DFS+DP (5) DP - Multi-Dimension (5) DP-Multiple Relation (5) Eulerian Cycle (5) Graph - Unusual (5) Graph Cycle (5) Hash Strategy (5) Immutability (5) Java (5) LogN (5) Manhattan Distance (5) Matrix Chain Multiplication (5) N Queens (5) Pre-Sort: Index (5) Quick Partition (5) Quora (5) Randomized Algorithms (5) Resources (5) Robot (5) SPFA(Shortest Path Faster Algorithm) (5) Shuffle (5) Sieve of Eratosthenes (5) Strongly Connected Components (5) Subarray Sum (5) Sudoku (5) Suffix Tree (5) Swap (5) Threaded (5) Tree - Creation (5) Warshall Floyd (5) Word Search (5) jiuzhang (5)

Popular Posts