Massive Algorithms: Leetcode 189

http://www.programcreek.com/2015/03/rotate-array-in-java/
Given an array of n elements, write an algorithm to rotate it right by k element without using any other array. In other words rotate an array in place.

Rotation of the above array by 2 will make array

we can rotate a string in O(n) time and O(1) extra space.
So the trick is to reverse the whole array first then reverse the array from 0 to k-1 and k to n-1.

https://leetcode.com/articles/rotate-array/

Given an array, rotate the array to the right by k steps, where k is non-negative.

Example 1:

Input: [1,2,3,4,5,6,7] and k = 3
Output: [5,6,7,1,2,3,4]
Explanation:
rotate 1 steps to the right: [7,1,2,3,4,5,6]
rotate 2 steps to the right: [6,7,1,2,3,4,5]
rotate 3 steps to the right: [5,6,7,1,2,3,4]

Example 2:

Input: [-1,-100,3,99] and k = 2
Output: [3,99,-1,-100]
Explanation: 
rotate 1 steps to the right: [99,-1,-100,3]
rotate 2 steps to the right: [3,99,-1,-100]

Note:

Try to come up as many solutions as you can, there are at least 3 different ways to solve this problem.
Could you do it in-place with O(1) extra space?

Approach #4 Using Reverse [Accepted]

    public void rotate(int[] nums, int k) {
        k %= nums.length;
        reverse(nums, 0, nums.length - 1);
        reverse(nums, 0, k - 1);
        reverse(nums, k, nums.length - 1);
    }
    public void reverse(int[] nums, int start, int end) {
        while (start < end) {
            int temp = nums[start];
            nums[start] = nums[end];
            nums[end] = temp;
            start++;
            end--;
        }
    }

Approach #3 Using Cyclic Replacements

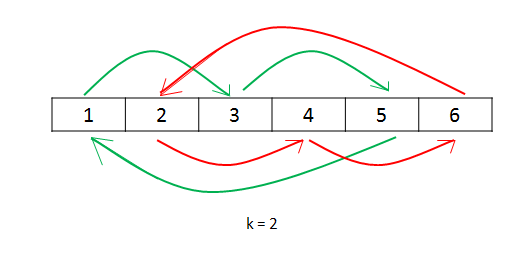
We can directly place every number of the array at its required correct position. But if we do that, we will destroy the original element. Thus, we need to store the number being replaced in a

temp

variable. Then, we can place the replaced number(

temp

) at its correct position and so on,

n

times, where

n

is the length of array. We have chosen

n

to be the number of replacements since we have to shift all the elements of the array(which is

n

). But, there could be a problem with this method, if

n

where

k = k

(since a value of

k

larger than

n

eventually leads to a

k

equivalent to

k

). In this case, while picking up numbers to be placed at the correct position, we will eventually reach the number from which we originally started. Thus, in such a case, when we hit the original number's index again, we start the same process with the number following it.

Now let's look at the proof of how the above method works. Suppose, we have

n

as the number of elements in the array and

k

is the number of shifts required. Further, assume

n

. Now, when we start placing the elements at their correct position, in the first cycle all the numbers with their index

i

satisfying

i

get placed at their required position. This happens because when we jump k steps every time, we will only hit the numbers k steps apart. We start with index

i=0

, having

i

. Thus, we hit all the numbers satisfying the above condition in the first cycle. When we reach back the original index, we have placed

\frac{n}{k}

elements at their correct position, since we hit only that many elements in the first cycle. Now, we increment the index for replacing the numbers. This time, we place other

\frac{n}{k}

elements at their correct position, different from the ones placed correctly in the first cycle, because this time we hit all the numbers satisfy the condition

i

. When we hit the starting number again, we increment the index and repeat the same process from

i=1

for all the indices satisfying

i

. This happens till we reach the number with the index

i

again, which occurs for

i=k

. We will reach such a number after a total of k cycles. Now, the total count of numbers exclusive numbers placed at their correct position will be

k \times \frac{n}{k}=n

. Thus, all the numbers will be placed at their correct position.

Look at the following example to clarify the process: nums: [1, 2, 3, 4, 5, 6] k: 2

    public void rotate(int[] nums, int k) {
        k = k % nums.length;
        int count = 0;
        for (int start = 0; count < nums.length; start++) {
            int current = start;
            int prev = nums[start];
            do {
                int next = (current + k) % nums.length;
                int temp = nums[next];
                nums[next] = prev;
                prev = temp;
                current = next;
                count++;
            } while (start != current);
        }
    }
}

https://discuss.leetcode.com/topic/11349/my-three-way-to-solve-this-problem-the-first-way-is-interesting-java

Here use a example input array [1,2,3,4,5,6,7,8] (n = 8) to explain:

suppose k = 3:

GCD = gcd(3,8) = 1, which means there is only one path.

Count = (n / GCD) - 1 = 7, which means we need 7 swaps to finish the path. (actually for a path have x element, we need x - 1 swaps)

Then we can simulate the process of the algorithm,

path0(each time swap index0 element and indexPosition element):

[1,2,3,4,5,6,7,8] (position = 3) -> [4,2,3,1,5,6,7,8] (position = 6) -> [7,2,3,1,5,6,4,8](position = 1) -> [2,7,3,1,5,6,4,8](position = 4) -> [5,7,3,1,2,6,4,8](position = 7) -> [8,7,3,1,2,6,4,5](position = 2) -> [3,7,8,1,2,6,4,5](position = 5) -> [6,7,8,1,2,3,4,5] -> finished, total 7 times swap. Final result [6,7,8,1,2,3,4,5]

suppose k = 2:

Similary, GCD = 2, which means there are 2 paths.

count = 3, which means we need 3 swaps to finish each path.

Give the process:

path0(swap index0 and position element):

[1,2,3,4,5,6,7,8](position = 2) -> [3,2,1,4,5,6,7,8](position = 4) ->[5,2,1,4,3,6,7,8](position = 6) -> [7,2,1,4,3,6,5,8] -> path0 finished

Then we continue processing path1(swap index1 and position element):

[7,2,1,4,3,6,5,8](position = 3) -> [7,4,1,2,3,6,5,8](position = 5) -> [7,6,1,2,3,4,5,8](position = 7) ->[7,8,1,2,3,4,5,6] -> path1 finished -> all path finished we get the result [7,8,1,2,3,4,5,6]

But I don't compute GCD and count of steps for each path. I just let it jumps from one path to another after finishing the previous path. And I didn't use swap() to process a path

    public void rotate(int[] nums, int k) {
        if(nums.length <= 1){
            return;
        }
        //step each time to move
        int step = k % nums.length;
        //find GCD between nums length and step
        int gcd = findGcd(nums.length, step);
        int position, count;
        
        //gcd path to finish movie
        for(int i = 0; i < gcd; i++){
            //beginning position of each path
            position = i;
            //count is the number we need swap each path
            count = nums.length / gcd - 1;
            for(int j = 0; j < count; j++){
                position = (position + step) % nums.length;
                //swap index value in index i and position
                nums[i] ^= nums[position];
                nums[position] ^= nums[i];
                nums[i] ^= nums[position];
            }
        }
    }
    
    public int findGcd(int a, int b){
        return (a == 0 || b == 0) ? a + b : findGcd(b, a % b);
    }

Approach #4 Using Reverse

    public void rotate(int[] nums, int k) {
        k %= nums.length;
        reverse(nums, 0, nums.length - 1);
        reverse(nums, 0, k - 1);
        reverse(nums, k, nums.length - 1);
    }
    public void reverse(int[] nums, int start, int end) {
        while (start < end) {
            int temp = nums[start];
            nums[start] = nums[end];
            nums[end] = temp;
            start++;
            end--;
        }
    }

Approach #2 Using Extra Array
We use an extra array in which we place every element of the array at its correct position i.e. the number at index

i

in the original array is placed at the index

(i + k)

. Then, we copy the new array to the original one.

    public void rotate(int[] nums, int k) {
        int[] a = new int[nums.length];
        for (int i = 0; i < nums.length; i++) {
            a[(i + k) % nums.length] = nums[i];
        }
        for (int i = 0; i < nums.length; i++) {
            nums[i] = a[i];
        }
    }

X. brute force

Time complexity : $O(n*k)$ . All the numbers are shifted by one step( $O(n)$ ) k times( $O(k)$ ).

The simplest approach is to rotate all the elements of the array in k steps by rotating the elements by 1 unit in each step.

    public void rotate(int[] nums, int k) {
        int temp, previous;
        for (int i = 0; i < k; i++) {
            previous = nums[nums.length - 1];
            for (int j = 0; j < nums.length; j++) {
                temp = nums[j];
                nums[j] = previous;
                previous = temp;
            }
        }

http://www.programcreek.com/2015/03/rotate-array-in-java/
需要注意的是，validate input， k可能会比nums.length更大。
Solution 1 - Intermediate Array
In a straightforward way, we can create a new array and then copy elements to the new array. Then change the original array by using System.arraycopy().

public void rotate(int[] nums, int k) {
    if(k > nums.length) 
        k=k%nums.length;
 
    int[] result = new int[nums.length];
 
    for(int i=0; i < k; i++){
        result[i] = nums[nums.length-k+i];
    }
 
    int j=0;
    for(int i=k; i<nums.length; i++){
        result[i] = nums[j];
        j++;
    }
 
    System.arraycopy( result, 0, nums, 0, nums.length );
}

Solution 2 - Bubble Rotate - O(N*K)

public static void rotate(int[] arr, int order) {
 if (arr == null || order < 0) {
     throw new IllegalArgumentException("Illegal argument!");
 }
 
 for (int i = 0; i < order; i++) {
  for (int j = arr.length - 1; j > 0; j--) {
   int temp = arr[j];
   arr[j] = arr[j - 1];
   arr[j - 1] = temp;
  }
 }
}

Solution 3 - Reversal

public static void rotate(int[] arr, int order) {
 order = order % arr.length;
 
 if (arr == null || order < 0) {
  throw new IllegalArgumentException("Illegal argument!");
 }
 
 //length of first part
 int a = arr.length - order; 
 
 reverse(arr, 0, a-1);
 reverse(arr, a, arr.length-1);
 reverse(arr, 0, arr.length-1);
 
}
 
public static void reverse(int[] arr, int left, int right){
 if(arr == null || arr.length == 1) 
  return;
 
 while(left < right){
  int temp = arr[left];
  arr[left] = arr[right];
  arr[right] = temp;
  left++;
  right--;
 } 
}

http://leetcode.com/2010/04/rotating-array-in-place.html

This is a trick so important that it becomes one of the frequently asked interview questions. An in-depth discussion is in Programming Pearls, one of the must-read book in Computer Science.

The trick is to do three reverse operation. One for the entire string, one from index 0 to k-1, and lastly index k to n-1. Magically, this will yield the correct rotated array, without any extra space!
http://www.geeksforgeeks.org/program-for-array-rotation-continued-reversal-algorithm/

void leftRotate(int arr[], int d, int n)

{

  rvereseArray(arr, 0, d-1);

  rvereseArray(arr, d, n-1);

  rvereseArray(arr, 0, n-1);

}

void rvereseArray(int arr[], int start, int end)

{

  int i;

  int temp;

  while(start < end)

{

    temp = arr[start];

    arr[start] = arr[end];

    arr[end] = temp;

    start++;

    end--;

}

}

Also refer to http://www.geeksforgeeks.org/program-for-array-rotation-continued-reversal-algorithm/
http://www.geeksforgeeks.org/array-rotation/

METHOD 3 (A Juggling Algorithm)
Time complexity: O(n)
Auxiliary Space: O(1)

Divide the array in different sets where number of sets is equal to GCD of n and d and move the elements within sets.
If GCD is 1 as is for the above example array (n = 7 and d =2), then elements will be moved within one set only, we just start with temp = arr[0] and keep moving arr[I+d] to arr[I] and finally store temp at the right place.

Here is an example for n =12 and d = 3. GCD is 3 and

Let arr[] be {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}
a) Elements are first moved in first set – (See below diagram for this movement)


          arr[] after this step --> {4 2 3 7 5 6 10 8 9 1 11 12}
b) Then in second set.
          arr[] after this step --> {4 5 3 7 8 6 10 11 9 1 2 12}
c) Finally in third set.
          arr[] after this step --> {4 5 6 7 8 9 10 11 12 1 2 3}

void leftRotate(int arr[], int d, int n)

{

  int i, j, k, temp;

  for (i = 0; i < gcd(d, n); i++)

{

    /* move i-th values of blocks */

    temp = arr[i];

    j = i;

    while(1)

{

      k = j + d;

      if (k >= n)

        k = k - n;

      if (k == i)

        break;

      arr[j] = arr[k];

      j = k;

}

    arr[j] = temp;

}

}

Block swap algorithm for array rotation O(n)

http://www.geeksforgeeks.org/block-swap-algorithm-for-array-rotation/

Initialize A = arr[0..d-1] and B = arr[d..n-1]
1) Do following until size of A is equal to size of B

  a)  If A is shorter, divide B into Bl and Br such that Br is of same 
       length as A. Swap A and Br to change ABlBr into BrBlA. Now A
       is at its final place, so recur on pieces of B.  
   b)  If A is longer, divide A into Al and Ar such that Al is of same 
       length as B Swap Al and B to change AlArB into BArAl. Now B
       is at its final place, so recur on pieces of A.
2)  Finally when A and B are of equal size, block swap them.

Recursive Implementation:

void leftRotate(int arr[], int d, int n)

{ 

  /* Return If number of elements to be rotated is 

    zero or equal to array size */ 

  if(d == 0 || d == n)

    return;

  /*If number of elements to be rotated is exactly 

    half of array size */ 

  if(n-d == d)

  {

    swap(arr, 0, n-d, d);   

    return;

  }  

 /* If A is shorter*/             

  if(d < n-d)

  {  

    swap(arr, 0, n-d, d);

    leftRotate(arr, d, n-d);    

  }    

  else /* If B is shorter*/             

  {

    swap(arr, 0, d, n-d);

    leftRotate(arr+n-d, 2*d-n, d); /*This is tricky*/

  }

}

/*This function swaps d elements starting at index fi

  with d elements starting at index si */

void swap(int arr[], int fi, int si, int d)

{

   int i, temp;

   for(i = 0; i<d; i++)   

   {

     temp = arr[fi + i];

     arr[fi + i] = arr[si + i];

     arr[si + i] = temp;

   }     

}    

Iterative Implementation:

void leftRotate(int arr[], int d, int n)

{

  int i, j;

  if(d == 0 || d == n)

    return;

  i = d;

  j = n - d;

  while (i != j)

  {

    if(i < j) /*A is shorter*/

    {

      swap(arr, d-i, d+j-i, i);

      j -= i;

    }

    else /*B is shorter*/

    {

      swap(arr, d-i, d, j);

      i -= j;

    }

    // printArray(arr, 7);

  }

  /*Finally, block swap A and B*/

  swap(arr, d-i, d, i);

}

METHOD 1 (Use temp array)

1) Store d elements in a temp array
2) Shift rest of the arr[]
3) Store back the d elements

Auxiliary Space: O(d)

METHOD 2 (Rotate one by one)

To rotate by one, store arr[0] in a temporary variable temp, move arr[1] to arr[0], arr[2] to arr[1] …and finally temp to arr[n-1]

Time complexity: O(n*d)
http://www.cs.bell-labs.com/cm/cs/pearls/s02b.pdf
http://www.fgdsb.com/2015/01/03/rotate-sorted-array/


void rotate_array(vector<int>& arr, int k) {


int n = (int)arr.size();


k = k % n;


if(k == 0) return;





int start = 0;


int tmp = arr[start];


for(int j = 0; j < n - 1; j++) {


int prev = (start + n - k) % n;


arr[start] = arr[prev];


start = prev;


}


arr[start] = tmp;


}

http://www.zrzahid.com/rotate-an-array/

public static void rotateRight(int[] A, int k){
 int n = A.length;
 if(n <= 1){
  return;
 }
 
 k = k%n;
 
 if(k == 0){
  return;
 }
 
 //reverse non rotated part
 reverse(A, 0, n-k-1);
 //reverse rotated part
 reverse(A, n-k, n-1);
 //reverse the whole array
 reverse(A, 0, n-1);
}

public static void rotateLeft(int[] A, int k){
 int n = A.length;
 if(n <= 1){
  return;
 }
 
 k = k%n;
 
 if(k == 0){
  return;
 }
 
 //reverse the whole array
 reverse(A, 0, n-1);
 //reverse rotated part
 reverse(A, n-k, n-1);
 //reverse non rotated part
 reverse(A, 0, n-k-1);
}

public static void reverse(int A[], int i, int j){
 while(i < j){
  swap(A, i, j);
  i++;
  j--;
 }
}

Let, n = length of array and d = number of rotations
so, we need to rotate right A by d%n.

So, position of the start of rotation k = n-(d%n)
initially i = 0, j = k, and we traverse left to right as follows - 

1, 2, 3, 4, 5, 6
^           ^
i           j,k       --> swap(i, j), increment i, j

5, 2, 3, 4, 1, 6      
   ^        ^  ^
   i        k  j      --> swap(i, j), increment i, j (j will be wrapped around k)

5, 6, 3, 4, 1, 2      
      ^     ^
      i     j,k       --> swap(i, j), increment i, j

5, 6, 1, 4, 3, 2      
         ^  ^  ^
         i  k  j      --> swap(i, j), increment i, j (j will be wrapped around k)

5, 6, 1, 2, 3, 4      
            ^
            i,j,k     --> we stop when i and j meet

public static void rotateRight(int[] A, int d){
 int n = A.length;
 
 int i = 0;
 int k = n - (d%n);
 int j = k;
 
 if(k < n/2){
  rotateLeft(A, n-d);
  return;
 }
 
 while(i < j){
  swap(A, i, j);
  i++;
  j = (j == n-1) ? k : j+1;
 }
}

public static void rotateLeft(int[] A, int d){
 int n = A.length;
 
 int i = n-1;
 int k = d%n-1;
 int j = k;
 
 if(k > n/2){
  rotateRight(A, n-d);
  return;
 }
 
 while(j < i){
  swap(A, i, j);
  i--;
  j = (j == 0) ? k : j-1;
 }
}

http://www.1point3acres.com/bbs/thread-207688-1-1.html
Read full article from Rotate an array right by k element without using any other array

Leetcode 189 - Rotate an array right by k element

Labels

Popular Posts