Given a collection of numbers that might contain duplicates, return all possible unique permutations.
Related: LeetCode 46 - Permutations
Related: LeetCode - Permutations
LeetCode - Subsets
For example, [1,1,2] have the following unique permutations:
[1,1,2], [1,2,1], and [2,1,1].
https://liweiwei1419.github.io/leetcode-solution/leetcode-0047-permutations-ii/
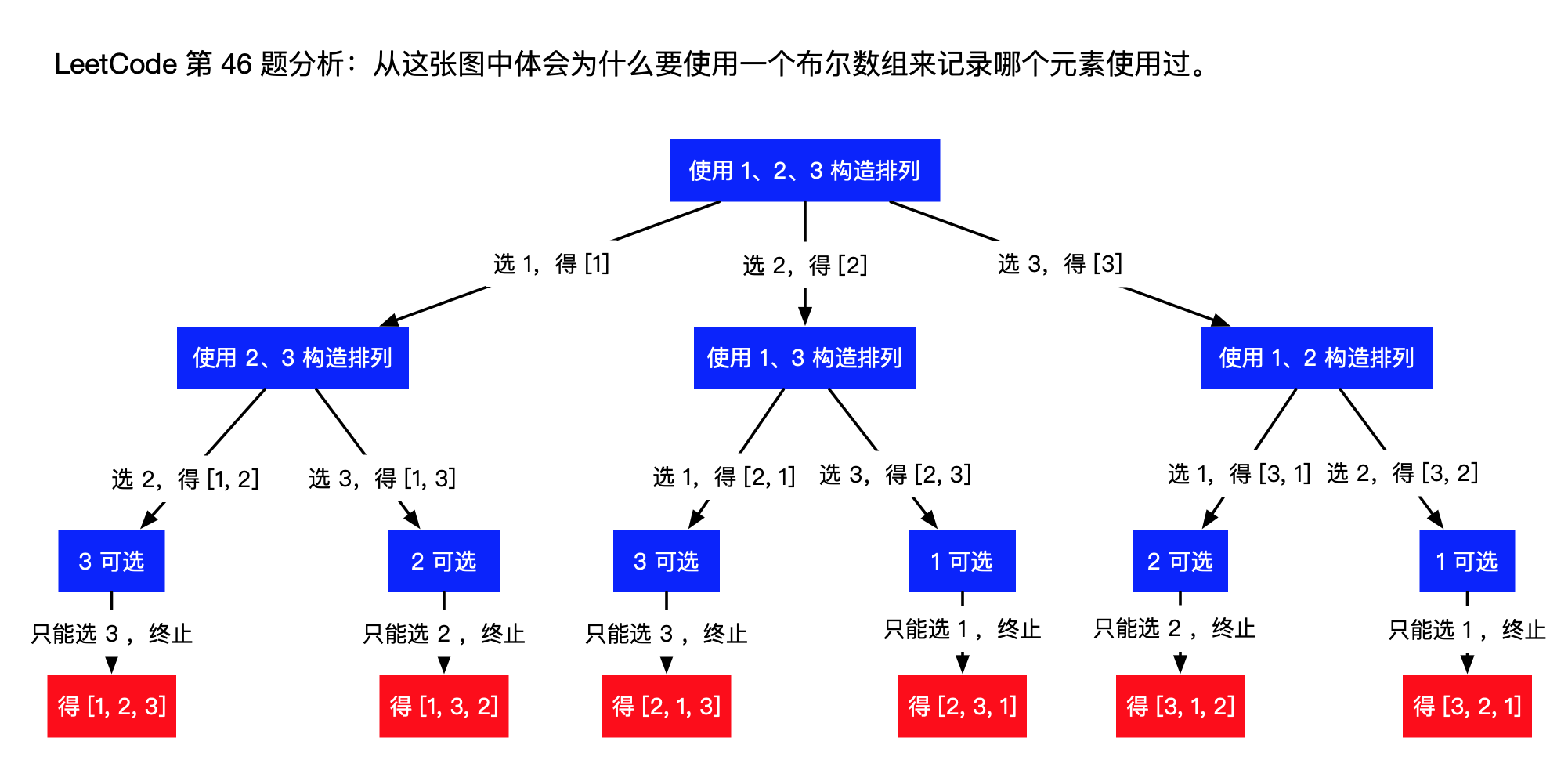

X. DFS
https://leetcode.com/problems/permutations-ii/discuss/18596/A-simple-C%2B%2B-solution-in-only-20-lines
https://cheonhyangzhang.wordpress.com/2015/09/22/47-leetcode-java-permutations-ii-medium/
X.
https://discuss.leetcode.com/topic/36221/share-my-java-code-with-detailed-explanantion
X. https://discuss.leetcode.com/topic/24347/short-and-fast-recursive-java-solution-easy-to-understand-with-explaination/
X. Without sort
http://cs-cjl.com/2016/10_13_leetcode_47_permutations_ii
Use HashMap
vector<vector<int> > permuteUnique(vector<int> &num) { vector<vector<int>> ret; vector<int> r; unordered_map<int, int> m; for (int i : num) { m[i]++; } permuteUnique(m, r, num.size(), ret); return ret; } void permuteUnique(unordered_map<int, int> &m, vector<int> &r, int remain, vector<vector<int>> &ret) { if (remain <= 0) { ret.push_back(r); return; } for (auto &p : m) { if (p.second <= 0) continue; p.second--; r.push_back(p.first); permuteUnique(m, r, remain - 1, ret); r.pop_back(); p.second++; } }
https://noahsnail.com/2018/12/12/2018-12-12-Leetcode-47--Permutations-II/
https://discuss.leetcode.com/topic/37030/java-iterative-solution-no-set-needed
Use set to remove dupicate
https://discuss.leetcode.com/topic/3170/accepted-iterative-solution-in-java
https://discuss.leetcode.com/topic/12923/short-iterative-java-solution
https://helloyuantechblog.wordpress.com/2015/10/16/leetcode-47-permutations-ii-medium/
In this case, it is more complicated, as duplicates exist. One common way to get rid of duplicates is to skip them whenever the first one is already tried out. To do this, we need to sort the array first, so that duplicates are adjacent to each other. Also, during the recursion, to generate the current possible permutation, we cannot simply swap the nums elements any more, as the swapping will make the array out of order. To compensate for that, we use an extra array to keep track of the current tried out elements; also as we cannot touch the nums, we use visited to record which ones in nums have we tried out.
http://yucoding.blogspot.com/2013/04/leetcode-question-70-permutations-ii.html
In this problem, what we need it to cut some of the subtrees. e.g. 122
122
/ | \
122 212 X (here because 2=2, we don't need to swap again)
/ \ / \
122 X 212 221
So, if there exist same element after current swap, there there is no need to swap again.
http://www.cnblogs.com/tenosdoit/p/3662644.html
在算法1的基础上,当我们枚举第i个位置的元素时,若要把后面第j个元素和i交换,则先要保证[i…j-1]范围内没有和位置j相同的元素。有以下两种做法(1)可以每次在需要交换时进行顺序查找;(2)用哈希表来查重。具体见下面的代码。
注意不要误以为以下两种做法能够去重:(1)最开始先对数组进行排序,以后每次交换时,只要保证当前要交换的元素和前一个元素不同,这种做法是错误的,虽然开始进行了排序,但是元素的交换会使数组再次变的无序(2)每次进入递归函数permuteRecur时,对从当前索引开始的子数组排序,这种做法也是错误的,因为每次交换元素后,我们要恢复交换的元素,如果在递归函数内排序,就不能正确的恢复交换的元素。
https://cheonhyangzhang.wordpress.com/2015/09/22/47-leetcode-java-permutations-ii-medium/
Related: LeetCode 46 - Permutations
Related: LeetCode - Permutations
LeetCode - Subsets
For example, [1,1,2] have the following unique permutations:
[1,1,2], [1,2,1], and [2,1,1].
https://liweiwei1419.github.io/leetcode-solution/leetcode-0047-permutations-ii/
求解关键:找到重复的原因,对树进行剪枝。 1、首先将数组排序,这一步很关键,是后面剪枝的基础; 2、只处理第 1 次遇到的那个数,举个具体的例子画个图。重点理解:(1)
i > 0 ,(2) nums[i] == nums[i - 1] ,(3)之前那个数还没有使用,即 marked[i-1] = false。

X. DFS
https://leetcode.com/problems/permutations-ii/discuss/18596/A-simple-C%2B%2B-solution-in-only-20-lines
vector<vector<int>> permuteUnique(vector<int>& nums) {
sort(nums.begin(), nums.end());
vector<vector<int>> perms;
permute(nums, 0, perms);
return perms;
}
private:
void permute(vector<int> nums, int start, vector<vector<int>>& perms) {
int n = nums.size();
if (start == n - 1) {
perms.push_back(nums);
} else {
for (int i = start; i < n; i++) {
if ((i == start) || (nums[i] != nums[start])) {
swap(nums[i], nums[start]);
permute(nums, start + 1, perms);
}
}
}
}
The for loop in recursion function keeps a loop invariant:
all the element after index
all the element after index
k remains sorted! Actually, the loop will explore all the possible way of keep element after k sorted.
As the recursion dive deep, we will explore all the possibility, and, of course, when we reach the end, the loop invariant told us that
we will be able to explore all the possible solution space. (Since there is no element after the last index).
we will be able to explore all the possible solution space. (Since there is no element after the last index).
Such a elegant solution. As those people mentioned before, we don't need to make a copy every time. We can recover the state, so we can still improve this
solution!
void recursion(vector<int>& nums, int begin, vector<vector<int>>& res){solution!
So the add condition is that for any duplicate elements, you only want to add it if the previous one ( duplicate) is added.
Say for 0 1 1, for the second 1, only insert it if the previous 1 is inserted so that we could avoid have two 0 1 1 permutation and 0 1 1 permutation.
X. DFS
private void findPermuteUnique(int[] nums, int depth, Stack<Integer> stack) {
if (depth == nums.length) {
res.add(new ArrayList<>(stack));
return;
}
for (int i = 0; i < nums.length; i++) {
if (!marked[i]) {
// i > 0 是为了保证 marked[i - 1] 有意义,事实上 i = 0 是一定在解当中的
// 相当于树被剪枝,重点体会这一步剪枝操作是为什么,其实画个图就非常清楚了
if (i > 0 && nums[i] == nums[i - 1] && !marked[i - 1]) {
continue;
}
marked[i] = true;
stack.add(nums[i]);
findPermuteUnique(nums, depth + 1, stack);
stack.pop();
marked[i] = false;
}
}
}
public List<List<Integer>> permuteUnique(int[] nums) {
int len = nums.length;
if (len == 0) {
return res;
}
// 这一步很关键,是后面剪枝的基础
Arrays.sort(nums);
marked = new boolean[len];
findPermuteUnique(nums, 0, new Stack<>());
return res;
}
If the collection contains duplicate, I cannot only use the original method I used in "46. Permutations", because it will produce duplicate permutations. For example, if the collection is [0, 1, 1], the result will contain two [0, 1, 1]s.
The idea is to maintain a rule about which one of the duplicate numbers can appear in the permutations. To do this, I can sort the array and make sure that only the number with a smaller index can appear in a duplicate permutation.
For example, as I add numbers to the permutation list, if I found that I'm adding the second 1 while the first 1 is not in the list, that means the first 1 has already been used to make the exact same permutation. So I continue to the next iteration.
https://leetcode.com/problems/permutations-ii/discuss/18594/Really-easy-Java-solution-much-easier-thanThe idea is to maintain a rule about which one of the duplicate numbers can appear in the permutations. To do this, I can sort the array and make sure that only the number with a smaller index can appear in a duplicate permutation.
For example, as I add numbers to the permutation list, if I found that I'm adding the second 1 while the first 1 is not in the list, that means the first 1 has already been used to make the exact same permutation. So I continue to the next iteration.
Use an extra boolean array " boolean[] used" to indicate whether the value is added to list.
Sort the array "int[] nums" to make sure we can skip the same value.
when a number has the same value with its previous, we can use this number only if his previous is used
跟 Permutations的解法一样,就是要考虑“去重”。先对数组进行排序,这样在DFS的时候,可以先判断前面的一个数是否和自己相等,相等的时候则前面的数必须使用了,自己才能使用,这样就不会产生重复的排列了。
Line 23: Don't miss “&& visited[i-1] ==0”. Or, the inner recursion will skip using duplicate number.
跟 Permutations的解法一样,就是要考虑“去重”。先对数组进行排序,这样在DFS的时候,可以先判断前面的一个数是否和自己相等,相等的时候则前面的数必须使用了,自己才能使用,这样就不会产生重复的排列了。
Line 23: Don't miss “&& visited[i-1] ==0”. Or, the inner recursion will skip using duplicate number.
public List<List<Integer>> permuteUnique(int[] nums) {
List<List<Integer>> res = new ArrayList<List<Integer>>();
if(nums==null || nums.length==0) return res;
boolean[] used = new boolean[nums.length];
List<Integer> list = new ArrayList<Integer>();
Arrays.sort(nums);
dfs(nums, used, list, res);
return res;
}
public void dfs(int[] nums, boolean[] used, List<Integer> list, List<List<Integer>> res){
if(list.size()==nums.length){
res.add(new ArrayList<Integer>(list));
return;
}
for(int i=0;i<nums.length;i++){
if(used[i]) continue;
if(i>0 &&nums[i-1]==nums[i] && !used[i-1]) continue;
used[i]=true;
list.add(nums[i]);
dfs(nums,used,list,res);
used[i]=false;
list.remove(list.size()-1);
}
}
The worst-case time complexity is O(n! * n).
- For any recursive function, the time complexity is O(branches^depth) * amount of work at each node in the recursive call tree. However, in this case, we have n*(n-1)*(n*2)*(n-3)*...*1 branches at each level = n!, so the total recursive calls is O(n!)
- We do n-amount of work in each node of the recursive call tree, (a) the for-loop and (b) at each leaf when we add n elements to an ArrayList. So this is a total of O(n) additional work per node.
Therefore, the upper-bound time complexity is O(n! * n).
We can do some optimizations on the above code:
- Only considering unique elements
- Add each unique element (as a key) and its frequency (as the value) to a Hash Table
- Iterate through each key of the Hash Table, and decrease the quantity of each element we use in each recursive call
Advantages of the optimized approach:
- Reduce the size of the for-loop -- rather than iterating through ALL of the elements of the array, we only need to iterate through the unique elements
- Sorting step also becomes unnecessary
- Minimize the space complexity; we don't need to allocate a huge array when we have many duplicates
Through some involved math we can probably derive a tighter upper bound for this approach, since we are doing less work at each level, e.g. n amount of work at each of the first level nodes, n-1 amount of work at each of the second level nodes, etc, but for our (interview) purposes the best upper bound is still the same, equal to O(n! * n).
https://leetcode.com/problems/permutations-ii/discuss/223854/Backtracking-solution-with-Map-using-Java public List<List<Integer>> permuteUnique(int[] nums) {
Arrays.sort(nums);
List<List<Integer>> listOfList = new ArrayList<>();
Map<Integer, Integer> map = new HashMap<Integer, Integer>();
for (int i = 0; i < nums.length; i++) {
if (!map.containsKey(nums[i])) map.put(nums[i], 1);
else map.put(nums[i], map.get(nums[i]) + 1);
}
findPermutation(nums, listOfList, new ArrayList<Integer>(), map);
return listOfList;
}
private void findPermutation(int[] nums, List<List<Integer>> listOfList, List<Integer> list, Map<Integer, Integer> map) {
if (list.size() == nums.length) {
listOfList.add(new ArrayList<Integer>(list));
return;
}
for(Integer i : map.keySet()) {
if (map.get(i) > 0) {
list.add(i);
map.put(i, map.get(i) - 1);
findPermutation(nums, listOfList, list, map);
map.put(i, map.get(i) + 1);
list.remove(list.size() - 1);
}
}
}
https://discuss.leetcode.com/topic/36221/share-my-java-code-with-detailed-explanantion
X. https://discuss.leetcode.com/topic/24347/short-and-fast-recursive-java-solution-easy-to-understand-with-explaination/
X. Without sort
什么时候会产生重复呢?
注意,上面一题中,我们每次都让0…start – 1固定,然后交换nums[i]和nums[start],接着继续递归下一层,然后恢复交换。
比如nums[i]有重复的元素,它之前的重复元素已经交换到start这个位置,那么之后nums[i]也要交换到start这个位置的话,那必然是重复的,因此我们可以记录一个数是不是被交换到start这个位置了。
只判断根据nums[i]和nums[start]是否相同判断是否重复是不够的,因为比如start的值为2,一开始交换到start的值为1,然后下一次交换过去的为1,两次都是判断2!=1.
void dfs(int start, vector<int> &nums, vector<vector<int>> &ans){
if(start == nums.size() - 1){
ans.push_back(nums);
return;
}
unordered_set<int> vis;
for(int i = start; i < nums.size(); ++i){
if(vis.find(nums[i]) != vis.end()) continue;
vis.insert(nums[i]);
swap(nums[i], nums[start]);
dfs(start + 1, nums, ans);
swap(nums[i], nums[start]);
}
}
public:
vector<vector<int>> permuteUnique(vector<int>& nums) {
vector<vector<int>> ans;
dfs(0, nums, ans);
return ans;
}
Use HashMap
vector<vector<int> > permuteUnique(vector<int> &num) { vector<vector<int>> ret; vector<int> r; unordered_map<int, int> m; for (int i : num) { m[i]++; } permuteUnique(m, r, num.size(), ret); return ret; } void permuteUnique(unordered_map<int, int> &m, vector<int> &r, int remain, vector<vector<int>> &ret) { if (remain <= 0) { ret.push_back(r); return; } for (auto &p : m) { if (p.second <= 0) continue; p.second--; r.push_back(p.first); permuteUnique(m, r, remain - 1, ret); r.pop_back(); p.second++; } }
X. Iterativevector<vector<int>> permuteUnique(vector<int>& nums) {vector<vector<int>> result;build(result, nums, 0);return result;}private:void build(vector<vector<int>>& result, vector<int>& nums, int start) {if(start == nums.size()) {result.push_back(nums);return;}unordered_set<int> duplicate;for(int i = start; i < nums.size(); i++) {int size = duplicate.size();duplicate.insert(nums[i]);if(size == duplicate.size()) {continue;}swap(nums[start], nums[i]);build(result, nums, start + 1);swap(nums[start], nums[i]);}}
https://discuss.leetcode.com/topic/37030/java-iterative-solution-no-set-needed
In each iteration, put the new number to all possible place.
To avoid duplicate we also have to:
To avoid duplicate we also have to:
- For duplicate numbers in a row, only add same number in in front of them.
- Break when same number exists in the permutation.
Use set to remove dupicate
https://discuss.leetcode.com/topic/3170/accepted-iterative-solution-in-java
public List<List<Integer>> permuteUnique(int[] num) {
Set<List<Integer>> permutations = new HashSet<List<Integer>>();
if(num.length > 0){
permutations.add(Arrays.asList(num[0]));
for(int index = 1; index < num.length; index++) {
Set<List<Integer>> newPermutations = new HashSet<List<Integer>>();
for(List<Integer> list : permutations){
for(int innerIndex = 0; innerIndex <= list.size(); innerIndex++){
List<Integer> newList = new ArrayList(list);
newList.add(innerIndex, num[index]);
newPermutations.add(newList);
}
}
permutations = newPermutations;
}
}
return new ArrayList<List<Integer>>(permutations);
}https://discuss.leetcode.com/topic/12923/short-iterative-java-solution
Here's an iterative solution which doesn't use nextPermutation helper. It builds the permutations for i-1 first elements of an input array and tries to insert the ith element into all positions of each prebuilt i-1 permutation. I couldn't come up with more effective controling of uniqueness than just using a Set.
public List<List<Integer>> permuteUnique(int[] num) {
LinkedList<List<Integer>> res = new LinkedList<>();
res.add(new ArrayList<>());
for (int i = 0; i < num.length; i++) {
Set<String> cache = new HashSet<>();
while (res.peekFirst().size() == i) {
List<Integer> l = res.removeFirst();
for (int j = 0; j <= l.size(); j++) {
List<Integer> newL = new ArrayList<>(l.subList(0,j));
newL.add(num[i]);
newL.addAll(l.subList(j,l.size()));
if (cache.add(newL.toString())) res.add(newL);
}
}
}
return res;
}https://helloyuantechblog.wordpress.com/2015/10/16/leetcode-47-permutations-ii-medium/
In this case, it is more complicated, as duplicates exist. One common way to get rid of duplicates is to skip them whenever the first one is already tried out. To do this, we need to sort the array first, so that duplicates are adjacent to each other. Also, during the recursion, to generate the current possible permutation, we cannot simply swap the nums elements any more, as the swapping will make the array out of order. To compensate for that, we use an extra array to keep track of the current tried out elements; also as we cannot touch the nums, we use visited to record which ones in nums have we tried out.
vector<vector<int> > permuteUnique(vector<int> &nums) { // write your code here vector<vector<int>> result; if (nums.empty()) { return result; } sort(nums.begin(), nums.end()); result.push_back(nums); int pos = 0; while(pos < nums.size()) { for(int i = result.size()-1; i >= 0; --i) { sort(result[i].begin()+pos, result[i].end()); for(int j = pos+1; j < nums.size(); ++j) { if (result[i][j] == result[i][j-1]) { continue; } swap(result[i][pos], result[i][j]); result.push_back(result[i]); swap(result[i][pos], result[i][j]); } } ++pos; } return result; }http://yucoding.blogspot.com/2013/04/leetcode-question-70-permutations-ii.html
In this problem, what we need it to cut some of the subtrees. e.g. 122
122
/ | \
122 212 X (here because 2=2, we don't need to swap again)
/ \ / \
122 X 212 221
So, if there exist same element after current swap, there there is no need to swap again.
http://www.cnblogs.com/tenosdoit/p/3662644.html
在算法1的基础上,当我们枚举第i个位置的元素时,若要把后面第j个元素和i交换,则先要保证[i…j-1]范围内没有和位置j相同的元素。有以下两种做法(1)可以每次在需要交换时进行顺序查找;(2)用哈希表来查重。具体见下面的代码。
注意不要误以为以下两种做法能够去重:(1)最开始先对数组进行排序,以后每次交换时,只要保证当前要交换的元素和前一个元素不同,这种做法是错误的,虽然开始进行了排序,但是元素的交换会使数组再次变的无序(2)每次进入递归函数permuteRecur时,对从当前索引开始的子数组排序,这种做法也是错误的,因为每次交换元素后,我们要恢复交换的元素,如果在递归函数内排序,就不能正确的恢复交换的元素。
https://cheonhyangzhang.wordpress.com/2015/09/22/47-leetcode-java-permutations-ii-medium/
Also http://shanjiaxin.blogspot.com/2014/02/permutations-ii-leetcode.html
This is similar to Permutations, the only difference is that the collection might contain duplicates.
So the modification is to avoid duplicate solution.
So the add condition is that for any duplicate elements, you only want to add it if the previous one ( duplicate) is added.
Say for 0 1 1, for the second 1, only insert it if the previous 1 is inserted so that we could avoid have two 0 1 1 permutation and 0 1 1 permutation.
Code from http://www.programcreek.com/2013/02/leetcode-permutations-ii-java/
For each number in the array, swap it with every element after it. To avoid duplicate, we need to check the existing sequence first.
http://www.cnblogs.com/springfor/p/3898447.html
Code from http://www.darrensunny.me/leetcode-permutations-ii/
with the use of a boolean array, do not consider to add a duplicate number to the next recursion if its earlier appearance has not been considered yet. This will avoid duplicate permutations.
跟 Permutations的解法一样,就是要考虑“去重”。先对数组进行排序,这样在DFS的时候,可以先判断前面的一个数是否和自己相等,相等的时候则前面的数必须使用了,自己才能使用,这样就不会产生重复的排列了。
void GeneratePermute(vector<int> & num, int step, vector<int>& visited, vector<int>& solution, vector<vector<int> >& coll)
{
if(step == num.size())
{
coll.push_back(solution);
return;
}
for(int i =0; i< num.size(); i++)
{
if(visited[i] == 0)
{
if(i>0 && num[i] == num[i-1] && visited[i-1] ==0)
continue;
visited[i] = 1;
solution.push_back(num[i]);
GeneratePermute(num, step+1, visited, solution, coll);
solution.pop_back();
visited[i] =0;
}
}
}
http://www.cnblogs.com/yuzhangcmu/p/4141085.html
用一个pre来记录选过的值,也可以达到同样的目的,只取第一个可以取到的位置,后面再取也是一样的解。用pre记下来,后面就不要再取同样的值了
Iteration Version:
Use set to maintain uniqueness:
https://github.com/allenlipeng47/algorithm/blob/master/src/main/java/com/pli/project/algorithm/array/Permutation3.java
http://www.lifeincode.net/programming/leetcode-permutations-and-permutations-ii-java/
We can start with computing the count of each letter (easy enough to get this-just use a hash table). For a string such as aabbbbc, this would be:
a->2 I b->4 I c->1
Let's imagine generating a permutation of this string (now represented as a hash table). The first choice we make is whether to use an a, b, or c as the first character. After that, we have a subproblem to solve: find all permutations of the remaining characters, and append those to the already picked "prefix:'
P(a->2 I b->4 I c->1) ={a + P(a->1 I b->4 I c->1)} +
{b + P(a->2 I b->3 I c->1)} +
{c + P(a->2 I b->4 I c->0)}
X. Use swap
https://leetcode.com/problems/permutations-ii/discuss/18609/Permutation-based-on-swap-beat-98
https://leetcode.com/problems/permutations-ii/discuss/18676/Swap-version-java
This happens because the if statement doesn't swap index and i if both have the same value. After the swap the value of index and i changes. So if you swap the values again you will not be repeating the numbers
So the modification is to avoid duplicate solution.
So the add condition is that for any duplicate elements, you only want to add it if the previous one ( duplicate) is added.
Say for 0 1 1, for the second 1, only insert it if the previous 1 is inserted so that we could avoid have two 0 1 1 permutation and 0 1 1 permutation.
public List<List<Integer>> permuteUnique(int[] num) { List<List<Integer>> result = new ArrayList<List<Integer>>(); Arrays.sort(num); Boolean[] visited = new Boolean[num.length]; for (int i = 0; i < visited.length; i ++){ visited[i] = false; } DFS(num, 0, result, new LinkedList<Integer>(), visited); return result; } private void DFS(int[] num, int togo, List<List<Integer>> result, List<Integer> current, Boolean[] visited ){ if (togo == visited.length){ result.add(new LinkedList(current)); } else{ for (int i = 0; i < num.length; i ++){ if (visited[i] == false){ if (i > 0 && num[i] == num[i-1] && visited[i-1] == false){ continue;//only insert duplicate element when the previous duplicate element has been inserted } current.add(num[i]); visited[i] = true; DFS(num, togo + 1, result, current, visited); current.remove(current.size() - 1); visited[i] = false; } }//for i }//else }//For each number in the array, swap it with every element after it. To avoid duplicate, we need to check the existing sequence first.
public ArrayList<ArrayList<Integer>> permuteUnique(int[] num) { ArrayList<ArrayList<Integer>> result = new ArrayList<ArrayList<Integer>>(); permuteUnique(num, 0, result); return result; } private void permuteUnique(int[] num, int start, ArrayList<ArrayList<Integer>> result) { if (start >= num.length ) { ArrayList<Integer> item = convertArrayToList(num); result.add(item); } for (int j = start; j <= num.length-1; j++) { if (notcontainsDuplicate(num, start, j)) { swap(num, start, j);//\\ permuteUnique(num, start + 1, result); swap(num, start, j);//\\ } } } private boolean notcontainsDuplicate(int[] arr, int start, int end) { for (int i = start; i <= end-1; i++) { if (arr[i] == arr[end]) { return false; } } return true; } |
1 public ArrayList<ArrayList<Integer>> permuteUnique(int[] num) {
2 ArrayList<ArrayList<Integer>> res = new ArrayList<ArrayList<Integer>>();
3 ArrayList<Integer> item = new ArrayList<Integer>();
4
5 if(num == null || num.length == 0)
6 return res;
7 boolean [] visited = new boolean[num.length];//
8 Arrays.sort(num);//
9 permutationhelper(res, num, item, visited, 0);
10 return res;
11 }
13 public void permutationhelper(ArrayList<ArrayList<Integer>> res, int[] num, ArrayList<Integer> item, boolean[] visited, int start){
14 if(item.size() == num.length){
15 res.add(new ArrayList<Integer>(item));
16 return;
17 }
18
19 for(int i = start; i < num.length; i++){
20 if(i > 0 && num[i] == num[i-1] && !visited[i - 1])
21 continue;
22 if(!visited[i]){
23 item.add(num[i]);
24 visited[i] = true;
25 permutationhelper(res, num, item, visited, start);
26 visited[i] = false;
27 item.remove(item.size()-1);
28 }
29 }
30 }
2 ArrayList<ArrayList<Integer>> res = new ArrayList<ArrayList<Integer>>();
3 ArrayList<Integer> item = new ArrayList<Integer>();
4
5 if(num == null || num.length == 0)
6 return res;
7 boolean [] visited = new boolean[num.length];//
8 Arrays.sort(num);//
9 permutationhelper(res, num, item, visited, 0);
10 return res;
11 }
13 public void permutationhelper(ArrayList<ArrayList<Integer>> res, int[] num, ArrayList<Integer> item, boolean[] visited, int start){
14 if(item.size() == num.length){
15 res.add(new ArrayList<Integer>(item));
16 return;
17 }
18
19 for(int i = start; i < num.length; i++){
20 if(i > 0 && num[i] == num[i-1] && !visited[i - 1])
21 continue;
22 if(!visited[i]){
23 item.add(num[i]);
24 visited[i] = true;
25 permutationhelper(res, num, item, visited, start);
26 visited[i] = false;
27 item.remove(item.size()-1);
28 }
29 }
30 }
public List<List<Integer>> permuteUnique(int[] num) {
List<List<Integer>> res=new ArrayList<List<Integer>>();
if(num==null || num.length==0) return res;
Arrays.sort(num);
boolean[] used=new boolean[num.length];
List<Integer> items= new ArrayList<Integer>();
helper(res,items,num,used);
return res;
}
public void helper(List<List<Integer>> res, List<Integer> items, int[] num, boolean[] used){
if(items.size()==num.length){
List<Integer> temp=new ArrayList<Integer>(items);
res.add(temp);
return;
}
for(int i=0;i<num.length;i++){
if(used[i]) continue;
used[i]=true;
items.add(num[i]);
helper(res,items,num,used);
used[i]=false;
items.remove(items.size()-1);
while(i+1<num.length && num[i+1]==num[i]) i++;
}
} bool noswap(int k, int i, const vector<int> num){ for (int j=k;j<i;j++){ if (num[j]==num[i]){ return true; } } return false; } void perm(vector<int> num,int k,int n, vector<vector<int> > &res){ if (k==n){ res.push_back(num); }else{ for (int i=k;i<=n;i++){ if (noswap(k,i,num)){continue;} int tmp = num[k]; num[k]=num[i]; num[i]=tmp; perm(num,k+1,n,res); tmp = num[k]; num[k]=num[i]; num[i]=tmp; } } } vector<vector<int> > permuteUnique(vector<int> &num) {\ vector<vector<int> > res; perm(num,0,(num.size()-1),res); return res; }Code from http://www.darrensunny.me/leetcode-permutations-ii/
with the use of a boolean array, do not consider to add a duplicate number to the next recursion if its earlier appearance has not been considered yet. This will avoid duplicate permutations.
跟 Permutations的解法一样,就是要考虑“去重”。先对数组进行排序,这样在DFS的时候,可以先判断前面的一个数是否和自己相等,相等的时候则前面的数必须使用了,自己才能使用,这样就不会产生重复的排列了。
public ArrayList<ArrayList<Integer>> permuteUnique(int[] num) {
if (num == null)
return null;
ArrayList<ArrayList<Integer>> result = new ArrayList<ArrayList<Integer>>();
if (num.length == 0)
return result;
Arrays.sort(num); // Sort the array in non-descending order
recursivePermute(num, new boolean[num.length], new ArrayList<Integer>(), result);
return result;
}
// If "current" is already a permutation of "num", add it to "result";
// otherwise, append each unused number to "current", and recursively try next unused number
private void recursivePermute(int[] num, boolean[] used, ArrayList<Integer> current,
ArrayList<ArrayList<Integer>> result) {
if (current.size() == num.length) { // "current" is already a permutation of "num"
result.add(new ArrayList<Integer>(current));
return;
}
// Append each unused number to "current", and recursively try next unused number
for (int i = 0; i < num.length; i++) {
if (i > 0 && !used[i-1] && num[i]==num[i-1])
// Do not consider a duplicate number if its earlier appearance has
// not been considered yet
continue;
if (!used[i]) {
// Append an unused number
used[i] = true;
current.add(num[i]);
// Recursively append next unused number
recursivePermute(num, used, current, result);
// Get back to original state, get ready for appending another unused number
current.remove(current.size()-1);
used[i] = false;
}
}
}
Code from http://fisherlei.blogspot.com/2012/12/leetcode-permutations-ii.htmlvoid GeneratePermute(vector<int> & num, int step, vector<int>& visited, vector<int>& solution, vector<vector<int> >& coll)
{
if(step == num.size())
{
coll.push_back(solution);
return;
}
for(int i =0; i< num.size(); i++)
{
if(visited[i] == 0)
{
if(i>0 && num[i] == num[i-1] && visited[i-1] ==0)
continue;
visited[i] = 1;
solution.push_back(num[i]);
GeneratePermute(num, step+1, visited, solution, coll);
solution.pop_back();
visited[i] =0;
}
}
}
http://www.cnblogs.com/yuzhangcmu/p/4141085.html
用一个pre来记录选过的值,也可以达到同样的目的,只取第一个可以取到的位置,后面再取也是一样的解。用pre记下来,后面就不要再取同样的值了
Iteration Version:
Use set to maintain uniqueness:
public static ArrayList<ArrayList<Integer>> permuteUnique(int[] num) { ArrayList<ArrayList<Integer>> returnList = new ArrayList<ArrayList<Integer>>(); returnList.add(new ArrayList<Integer>()); for (int i = 0; i < num.length; i++) { Set<ArrayList<Integer>> currentSet = new HashSet<ArrayList<Integer>>(); for (List<Integer> l : returnList) { for (int j = 0; j < l.size() + 1; j++) { l.add(j, num[i]); ArrayList<Integer> T = new ArrayList<Integer>(l); l.remove(j); currentSet.add(T); } } returnList = new ArrayList<ArrayList<Integer>>(currentSet); } return returnList; }
https://github.com/allenlipeng47/algorithm/blob/master/src/main/java/com/pli/project/algorithm/array/Permutation3.java
http://www.lifeincode.net/programming/leetcode-permutations-and-permutations-ii-java/
One simple way of handling this problem is to do the same work to check if a permutation has been created before and then, if not, add it to the list. A simple hash table will do the trick here. This solution will take O(n ! ) time in the worst case (and, in fact in all cases).
We can start with computing the count of each letter (easy enough to get this-just use a hash table). For a string such as aabbbbc, this would be:
a->2 I b->4 I c->1
Let's imagine generating a permutation of this string (now represented as a hash table). The first choice we make is whether to use an a, b, or c as the first character. After that, we have a subproblem to solve: find all permutations of the remaining characters, and append those to the already picked "prefix:'
P(a->2 I b->4 I c->1) ={a + P(a->1 I b->4 I c->1)} +
{b + P(a->2 I b->3 I c->1)} +
{c + P(a->2 I b->4 I c->0)}
Arraylist<String> printPerms(String s) {
Arraylist<String> result = new Arraylist<String>();
HashMap<Character, Integer> map = buildFreqTable(s);
printPerms(map, '"', s.length(), result);
return result;
}
HashMap<Character, Integer> buildFreqTable(String s) {
HashMap<Character, Integer> map= new HashMap<Character, Integer>();
for (char c : s.toCharArray()) {
if (!map.containsKey(c)) {
map.put(c, 0);
}
map.put(c, map.get(c) + 1);
}
return map;
}
void printPerms(HashMap<Character, Integer> map, String prefix, int remaining,
ArrayList<String> result) {
/* Base case. Permutation has been completed. */
if (remaining== 0) {
result.add(prefix);
return;
}
/* Try remaining letters for next char, and generate remaining permutations. */
for (Character c : map.keySet()) {
int count= map.get(c);
if (count > 0) {
map.put(c, count - 1);
printPerms(map, prefix + c, remaining - 1, result);
map.put(c, count);
}
}
}
X. Use swap
https://leetcode.com/problems/permutations-ii/discuss/18609/Permutation-based-on-swap-beat-98
public List<List<Integer>> permuteUnique(int[] nums) {
Arrays.sort(nums);
List<List<Integer>> res = new ArrayList<>();
permute(nums, 0, res);
return res;
}
private void permute(int[] nums, int pos, List<List<Integer>> res){
if(pos>=nums.length){
List<Integer> list = new ArrayList<>();
for(int num : nums) {
list.add(num);
}
res.add(list);
return;
}
for(int i=pos; i<nums.length; i++){
if(i!=pos && (nums[i]==nums[i-1] || nums[pos]==nums[i])) continue;
swap(nums, i, pos);
permute(nums, pos+1, res);
}
for ( int i = pos; i+1 < nums.length; i++ ) {
swap(nums, i, i+1);
}
}
private void swap(int[] nums, int i, int j){
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
public List<List<Integer>> permuteUnique(int[] nums) {
Arrays.sort(nums);
List<List<Integer>> res = new ArrayList<>();
if(nums == null|| nums.length == 0) res.add(new ArrayList<Integer>());
helper(res, nums, 0);
return res;
}
private void helper(List<List<Integer>> res, int[] nums, int index){
if(index == nums.length){
List<Integer> list = new ArrayList<>();
for(int num : nums){
list.add(num);
}
res.add(list);
return;
}
for(int i = index; i < nums.length; i++ ){
if(i > index && nums[i] == nums[index]) continue;
swap(nums, index, i);
helper(res, Arrays.copyOf(nums, nums.length), index+1);
}
}
private void swap(int[] a, int i , int j){
int tmp = a[i];
a[i] = a[j];
a[j] = tmp;
}
A quick note. You don't have to sort the array initially if you swap index and i again inside the for loop after calling the helper function.
for(int i = index; i < nums.length; i++ ){
if(i > index && nums[i] == nums[index]) continue;
swap(nums, index, i);
helper(res, Arrays.copyOf(nums, nums.length), index+1);
swap(nums,index,i);
}