LeetCode 46 - Permutations


LeetCode - Subsets
Related: LeetCode 47 - Permutations II
Given a collection of numbers, return all possible permutations.
For example, [1,2,3] have the following permutations:
[1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], and [3,2,1]
http://yucoding.blogspot.com/2013/04/leetcode-question-69-permutations.html
Consider:
a --> a
ab --> ab, ba
abc --> abc, acb, bac, bca, cab, cba.
...
where for the length of n, the permutations can be generated by
(1) Swap the 1st element with all the elements, including itself.
       (2) Then the 1st element is fixed, go to the next element.
       (3) Until the last element is fixed. Output.
Iterative Version
Loop through the array, in each iteration, a new number is added to different locations of results of previous iteration. Start from an empty List.
https://discuss.leetcode.com/topic/10812/share-my-short-iterative-java-solution
就是遍历nums（第一个for loop），当开始进行nums[i]时，res中的结果是nums[0]至nums[i-1]的全排列。每一次循环中，需要将nums[i]加入到res中的每一个结果中的每一个位置，然后开始下一次循环。具体做法是，每一次循环开始，先记录当前res的大小（size），取出res中的第一个，在每个位置添加nums[i]然后加到res末尾（第三个for loop，循环r.size()次），一共进行size次（第二个for loop）
t.add(i, n); is very expensive. The time complexity is O(n!*n)
public List<List<Integer>> permute(int[] num) {
    LinkedList<List<Integer>> res = new LinkedList<List<Integer>>();
    res.add(new ArrayList<Integer>());
    for (int n : num) {
        int size = res.size();
        for (; size > 0; size--) {
            List<Integer> r = res.pollFirst();
            for (int i = 0; i <= r.size(); i++) {
                List<Integer> t = new ArrayList<Integer>(r);
                t.add(i, n);
                res.add(t);
            }
        }
    }
    return res;
}
https://discuss.leetcode.com/topic/6377/my-ac-simple-iterative-java-python-solution
https://discuss.leetcode.com/topic/10812/share-my-short-iterative-java-solution
the basic idea is, to permute n numbers, we can add the nth number into the resulting List<List<Integer>> from the n-1 numbers, in every possible position.
For example, if the input num[] is {1,2,3}: First, add 1 into the initial List<List<Integer>> (let's call it "answer").
Then, 2 can be added in front or after 1. So we have to copy the List<Integer> in answer (it's just {1}), add 2 in position 0 of {1}, then copy the original {1} again, and add 2 in position 1. Now we have an answer of {{2,1},{1,2}}. There are 2 lists in the current answer.
Then we have to add 3. first copy {2,1} and {1,2}, add 3 in position 0; then copy {2,1} and {1,2}, and add 3 into position 1, then do the same thing for position 3. Finally we have 2*3=6 lists in answer, which is what we want.
public List<List<Integer>> permute(int[] num) {
    List<List<Integer>> ans = new ArrayList<List<Integer>>();
    if (num.length ==0) return ans;
    List<Integer> l0 = new ArrayList<Integer>();
    l0.add(num[0]);
    ans.add(l0);
    for (int i = 1; i< num.length; ++i){
        List<List<Integer>> new_ans = new ArrayList<List<Integer>>(); 
        for (int j = 0; j<=i; ++j){            
           for (List<Integer> l : ans){
            List<Integer> new_l = new ArrayList<Integer>(l);
            new_l.add(j,num[i]);
            new_ans.add(new_l);
           }
        }
        ans = new_ans;
    }
    return ans;
}

 与subset I的方法2很相近。以题中例子说明：
当只有1时候：[1]
当加入2以后：[2, 1], [1, 2]
当加入3以后：[3, 2, 1], [2, 3, 1], [2, 1, 3], [3, 1, 2], [1, 3, 2], [1, 2, 3]
前3个permutation分别对应将3插入[2, 1]的0, 1, 2的位置。同理后3个为插入[1, 2]的。因此可以用逐个插入数字来构造所有permutation.
[leetcode] Permutations | 一个array的所有permutation
public ArrayList<ArrayList<Integer>> permute(int[] num) {
  ArrayList<ArrayList<Integer>> lastLayer = new ArrayList<ArrayList<Integer>>();
  lastLayer.add(new ArrayList<Integer>());
  for (int i = 0; i < num.length; i++) {
    ArrayList<ArrayList<Integer>> newLayer = new ArrayList<ArrayList<Integer>>();
    for (int j = 0; j < lastLayer.size(); j++) {
      ArrayList<Integer> curr = lastLayer.get(j);
      insertEverywhere(curr, num[i], newLayer);
    }
    lastLayer = newLayer; // switch pointers instead of copy
  }
  return lastLayer;
}
private void insertEverywhere(ArrayList<Integer> curr, int num, ArrayList<ArrayList<Integer>> newLayer) {
  for (int i = 0; i <= curr.size(); i++) {
    ArrayList<Integer> newList = new ArrayList<Integer>(curr);
    newList.add(i, num);
    newLayer.add(newList);
   }
}
Code from http://www.programcreek.com/2013/02/leetcode-permutations-java/
public ArrayList<ArrayList<Integer>> permute(int[] num) {
 ArrayList<ArrayList<Integer>> result = new ArrayList<ArrayList<Integer>>();
 
 //start from an empty list
 result.add(new ArrayList<Integer>());
 
 for (int i = 0; i < num.length; i++) {
  //list of list in current iteration of the array num
  ArrayList<ArrayList<Integer>> current = new ArrayList<ArrayList<Integer>>();
 
  for (ArrayList<Integer> l : result) {
   // # of locations to insert is largest index + 1
   for (int j = 0; j < l.size()+1; j++) {
    ArrayList<Integer> temp = new ArrayList<Integer>(l);
                                temp .add(j, num[i]);


    current.add(temp);
   }
  }
 
  result = new ArrayList<ArrayList<Integer>>(current);
 }
 
 return result;
}
http://blog.csdn.net/linhuanmars/article/details/21569031
上面的代码有时候乍一看可能觉得只有两层循环，时间复杂度是不是O(n^2)之类的。事实上肯定不是的，因为注意第二层循环是对于res进行遍历的，而res是一直在以平方量级增长的，所以总的时间复杂度还是会是指数量级以上的。
https://leetcode.com/discuss/19510/my-ac-simple-iterative-java-python-solution
the basic idea is, to permute n numbers, we can add the nth number into the resultingList<List<Integer>> from the n-1 numbers, in every possible position.
For example, if the input num[] is {1,2,3}: First, add 1 into the initial List<List<Integer>> (let's call it "answer").
Then, 2 can be added in front or after 1. So we have to copy the List in answer (it's just {1}), add 2 in position 0 of {1}, then copy the original {1} again, and add 2 in position 1. Now we have an answer of {{2,1},{1,2}}. There are 2 lists in the current answer.

Then we have to add 3. first copy {2,1} and {1,2}, add 3 in position 0; then copy {2,1} and {1,2}, and add 3 into position 1, then do the same thing for position 3. Finally we have 2*3=6 lists in answer, which is what we want.
we can optimize the solution by adding on to a single answer list instead of recreating a new list every time!

X. DFS
https://discuss.leetcode.com/topic/46162/a-general-approach-to-backtracking-questions-in-java-subsets-permutations-combination-sum-palindrome-partioning
Bottom up approach
https://discuss.leetcode.com/topic/23036/java-clean-code-two-recursive-solutions
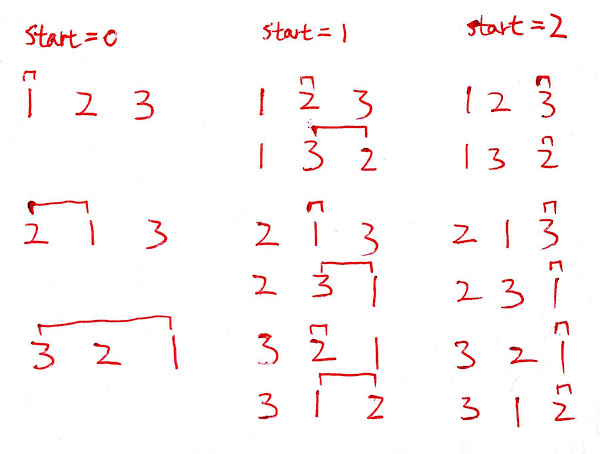
Code flow
nums = 1,2,3

start = 0, permutation = []
i = 0, newPermutation = [1]
 start = 1, permutation = [1]
 i = 0, newPermutation = [2, 1]
  start = 2, permutation = [2, 1]
  i = 0, newPermutation = [3, 2, 1]
  i = 1, newPermutation = [2, 3, 1]
  i = 2, newPermutation = [2, 1, 3]
 i = 1, newPermutation = [1, 2]
  start = 2, permutation = [1, 2]
  i = 0, newPermutation = [3, 1, 2]
  i = 1, newPermutation = [1, 3, 2]
  i = 2, newPermutation = [1, 2, 3]
https://leetcode.com/discuss/29483/share-my-short-iterative-java-solution
public class Solution { public List<List<Integer>> permute(int[] nums) { List<List<Integer>> result = new LinkedList<List<Integer>>(); if(nums.length == 0) return result; List<Integer> cur = new LinkedList<Integer>(); cur.add(nums[0]); result.add(cur); for(int i = 1; i < nums.length; i++) { int curSize = result.size(); for(int j = 0; j < curSize; j++) { for(int x = 0; x < result.get(j).size(); x++) { List<Integer> newList = new LinkedList<Integer>(result.get(j)); newList.add(x, nums[i]); result.add(newList); } result.get(j).add(nums[i]); } } return result; } }
I used your idea of adding each next value to every possible position of current list, but have done it with recursion. -- not

public List<List<Integer>> permute(int[] nums) {
    List<List<Integer>> result = new ArrayList<List<Integer>>();
    if (nums.length == 0) return result;

    backtrack(result, nums, new ArrayList<Integer>(), 0);

    return result;
}

private void backtrack(List<List<Integer>> result, int[] nums, List<Integer> currentList, int index) {
    if (currentList.size() == nums.length) {
        result.add(currentList);
        return;
    }

    int n = nums[index];
    for (int i = 0; i <= currentList.size(); i++) {
        List<Integer> copy = new ArrayList<Integer>(currentList);
        copy.add(i, n);
        backtrack(result, nums, copy, index + 1);
    }


}
https://leetcode.com/discuss/18212/my-elegant-recursive-c-solution-with-inline-explanation
http://xiaohuiliucuriosity.blogspot.com/2014/12/permutations.html
Recursive Version:
==> no need end as end never changes

    public List<List<Integer>> permute(int[] num) {
        List<List<Integer>> result = new ArrayList<List<Integer>>();
        permute(result, num, 0);
        return result;
    }
    
    private void permute(List<List<Integer>> result, int[] array, int start) {
  if (start >= array.length) {
   List<Integer> current = new ArrayList<Integer>();
   for (int a : array) {
       current.add(a);
   }
   result.add(current);
  } else {
   for (int i=start; i<array.length; i++) {
    swap(array, start, i);
    permute(result, array, start+1);
    swap(array, start, i);
   }
  }
 }
 
 private void swap(int[] array, int i, int j) {
  int temp = array[i];
  array[i] = array[j];
  array[j] = temp;
 }
I enumerate all the permutations in a generative way, the idea is that, at each position, I specify the element by swapping with values with a larger index. The value at the first position can swap with position 1,2,...,n-1, after each swap, I will do a recursion for the rest of the array.
The problem is that with this approach, the permutations may be out of order.


https://discuss.leetcode.com/topic/46162/a-general-approach-to-backtracking-questions-in-java-subsets-permutations-combination-sum-palindrome-partioning
We can also recursively solve this problem. Swap each element with each element after it.
public ArrayList<ArrayList<Integer>> permute(int[] num) {
 ArrayList<ArrayList<Integer>> result = new ArrayList<ArrayList<Integer>>();
 permute(num, 0, result);
 return result;
}
 
void permute(int[] num, int start, ArrayList<ArrayList<Integer>> result) {
 
 if (start >= num.length) {
  ArrayList<Integer> item = new ArrayList(num);
  result.add(item);
 }
 
 for (int j = start; j <= num.length - 1; j++) {
  swap(num, start, j); //\\ key
  permute(num, start + 1, result);
  swap(num, start, j); //\\
 }
}
private void swap(int[] a, int i, int j) {
 int temp = a[i];
 a[i] = a[j];
 a[j] = temp;
}
X. Use boolean visited array: add/remove
code from http://blog.csdn.net/u010500263/article/details/18178243

  public ArrayList<ArrayList<Integer>> permute(int[] num) {



    ArrayList<ArrayList<Integer>> result = new ArrayList<ArrayList<Integer>>();



    ArrayList<Integer> element = new ArrayList<Integer>();



    boolean[] visited = new boolean[num.length];



    helper(num, result, element, visited);



    return result;



  }







  public void helper(int[] num, ArrayList<ArrayList<Integer>> result, ArrayList<Integer> element, boolean[] visited) {



    if (element.size() == num.length) {



      // duplicate element and add it to result (element would be changed from time to



      // time. If directly use element



      // only result would be changed when element changed)



      result.add(new ArrayList<Integer>(element));



      return;



    }







    for (int i = 0; i < num.length; i++) {



      if (!visited[i]) {



        visited[i] = true;



        element.add(num[i]);



        helper(num, result, element, visited);







        // After providing a complete permutation, pull out the last number,



        element.remove(element.size() - 1);



        visited[i] = false;



      }



    }



  }


https://leetcode.com/discuss/55418/java-clean-code-two-recursive-solutions
public class Solution {
   public List<List<Integer>> permute(int[] nums) {
        List<List<Integer>> permutations = new ArrayList<>();
        if (nums.length == 0) {
            return permutations;
        }

        collectPermutations(nums, 0, new ArrayList<>(), permutations);
        return permutations;
    }

    private void collectPermutations(int[] nums, int start, List<Integer> permutation,
            List<List<Integer>>  permutations) {

        if (permutation.size() == nums.length) {
            permutations.add(permutation);
            return;
        }

        for (int i = 0; i <= permutation.size(); i++) {
            List<Integer> newPermutation = new ArrayList<>(permutation);
            newPermutation.add(i, nums[start]);
            collectPermutations(nums, start + 1, newPermutation, permutations);
        }
    }
}
https://leetcode.com/problems/permutations/discuss/18459/Java-solution-easy-to-understand-(backtracking)
List<List<Integer>> list; public List<List<Integer>> permute(int[] nums) { list = new ArrayList<>(); ArrayList<Integer> perm = new ArrayList<Integer>(); backTrack(perm,0,nums); return list; } void backTrack (ArrayList<Integer> perm,int i,int[] nums){ //Permutation completes if(i==nums.length){ list.add(new ArrayList(perm)); return; } ArrayList<Integer> newPerm = new ArrayList<Integer>(perm); //Insert elements in the array by increasing index for(int j=0;j<=i;j++){ newPerm.add(j,nums[i]);// this is slow backTrack(newPerm,i+1,nums); newPerm.remove(j); } }
X. DFS
这种思路和思路1的区别是：思路1采用位置两两交换，交换后出现一种新的组合，将这种新的组合添加到中间集，再添加到结果集中。而这种思路是采用逐一向中间集添加元素，并将当中间集元素个数等于 nums 长度的时候，将中间集添加到结果集中，并终止该层递归：

  public List<List<Integer>> permute(int[] nums) {
    List<List<Integer>> res = new ArrayList<>();
    dfs(res, new ArrayList<Integer>(), nums, new boolean[nums.length]);
    return res;
  }

  private void dfs(List<List<Integer>> res, List<Integer> temp, int[] nums, boolean[] used) {
    if (temp.size() == nums.length) {
      res.add(new ArrayList<>(temp));
      return;
    }
    for (int i = 0; i < nums.length; i++) {
      if (!used[i]) {
        used[i] = true;
        temp.add(nums[i]);
        dfs(res, temp, nums, used);
        temp.remove(temp.size() - 1);
        used[i] = false;
      }
    }
  }
X. Base case and build approach
https://discuss.leetcode.com/topic/23036/java-clean-code-two-recursive-solutions
   public List<List<Integer>> permute(int[] nums) {
  return permute(Arrays.stream(nums).boxed().collect(Collectors.toList()));
   }

 private List<List<Integer>> permute(List<Integer> nums) {
  List<List<Integer>> permutations = new ArrayList<>();
  if (nums.size() == 0) {
   return permutations;
  }
  if (nums.size() == 1) {
   List<Integer> permutation = new ArrayList<>();
   permutation.add(nums.get(0));
   permutations.add(permutation);
   return permutations;
  }
  
  List<List<Integer>> smallPermutations = permute(nums.subList(1, nums.size()));
  int first = nums.get(0);
  for(List<Integer> permutation : smallPermutations) {
   for (int i = 0; i <= permutation.size(); i++) {
    List<Integer> newPermutation = new ArrayList<>(permutation);
    newPermutation.add(i, first);
    permutations.add(newPermutation);
   }
  }
  return permutations;
 }
X. http://www.geeksforgeeks.org/permutations-string-using-iteration/
Concept Used : We keep swapping a character only till it reaches the end
  1. Fix ‘a’. Swap ‘b’ with its next neighbors till b reaches the end.
    ( “acbd”, “acdb”)
  2. Now ‘c’ will be at the 2nd position, do the same thing with it.
    ( “adcb”, “adbc”)
  3. Now ‘d’ will be at the 2nd position, do the same thing with it.
    ( “abdc”, “abcd”)
  4. All 6 i.e., (4!/4)permutations of the first cycle obtained.
  5. Repeat the above process by bringing swapping ‘a’ with ‘b’
  6. The new string to “play” will be “bacd”.
// A utility function to find n!
int fact(int n)
{
    return (n==1)? 1 : n*fact(n-1);
}
// An iterative function to print all permutations of s.
void printPermutation(string s)
{
    // Find length of string and factorial of length
    int n = s.length();
    int fc = fact(n);
    // Point j to the 2nd position
    int j = 1;
    // To store position of character to be fixed next.
    // m is used as in index in s[].
    int m = 0;
    // Iterate while permutation count is
    // smaller than n! which fc
    for (int perm_c = 0; perm_c < fc; )
    {
        // Store perm as current permutation
        string perm = s;
        // Fix the first position and iterate (n-1)
        // characters upto (n-1)!
        // k is number of iterations for current first
        // character.
        int k = 0;
        while (k != fc/n)
        {
            // Swap jth value till it reaches the end position
            while (j != n-1)
            {
                // Print current permutation
                cout << perm << "\n";
                // Swap perm[j] with next character
                swap(perm[j], perm[j+1]);
                // Increment count of permutations for this
                // cycle.
                k++;
                // Increment permutation count
                perm_c++;
                // Increment 'j' to swap with next character
                j++;
            }
            // Again point j to the 2nd position
            j = 1;
        }
        // Move to next character to be fixed in s[]
        m++;
        // If all characters have been placed at
        if (m == n)
           break;
        // Move next character to first position
        swap(s[0], s[m]);
    }
}
Also refer to http://blog.csdn.net/u010500263/article/details/18178243
http://yucoding.blogspot.com/2013/04/leetcode-question-69-permutations.html


Approach 1: Building from permutations of first n-1 characters.
Arraylist<String> getPerms(String str) {
        if (str == null) return null;

        Arraylist<String> permutations new ArrayList<String>();
        if (str.length() == 0) {//base case
                permutations.add('"');
                return permutations;
        }

        char first= str.charAt(0); // get the first char
        String remainder= str.substring(l); // remove the first char
        Arraylist<String> words= getPerms(remainder);
        for (String word: words) {
                for (int j = 0; j <= word.length(); +j +) {
                        String s= insertCharAt(word, first, j);
                        permutations.add(s);
                }
        }
        return permutations;
}
/* Insert char c at index i in word. */
String insertCharAt(String word, char c, int i) {
        String start= word.substring(0, i);
        String end= word.substring(i);
        return start+ c + end;
}


Approach 2: Building from permutations of all n-1 character substrings.
we just need to "try" each character as the first character and then append the permutations.
P(a1 a2a3 ) = {a1 + P(a2a3 )} + a2 + P(a1a)} + {a3 + P(a1a2 )}
{a1 + P(a2a3 )} -> a1a2a3 , a1a3 a2
{ a2 + P( a1a)} - > a2 a1 a3 , a2 a3a1
{a3 + P(a1 a)} -> a3 a1 a2 , a3 a2 a1
P(a1a2a3 a4 ) = {a1 + P(a2a3a4 )} + {a2 + P(a1a,a4 )} + {a, + P(a1a2a4 )} + {a4 + P(a1a2a,)}
Arraylist<String> getPerms(String remainder) {
        int len - remainder.length();
        ArrayList<String> result= new ArrayList<String>();
        /* Base case. */
        if (len == 0) {
        }
        result.add(""); // Be sure to return empty string!
        return result;
        for (int i= 0; i < len; i++) {
                /* Remove char i and find permutations of remaining chars.*/
                String before= remainder.substring(0, i);
                String after = remainder.substring(i + 1, len);
                Arraylist<String> partials = getPerms(before + after);
                /* Prepend char i to each permutation.*/
                for (String s : partials) {
                        result.add(remainder.charAt(i) + s);
                }
        }
        return result;
}

Arraylist<String> getPerms(String str) {
        Arraylist<String> result = new Arraylist<String>();
        getPerms("", str, result);
        return result;
}

void getPerms(String prefix, String remainder, Arraylist<String> result) {
        if (remainder.length()== 0) result.add(prefix);

        int len = remainder.length();
        for (int i= 0; i < len; i++) {
                String before = remainder.substring(0, i);
                String after = remainder.substring(i + 1, len);
                char c = remainder.charAt(i);
                getPerms(prefix + c, before + after, result);
        }
}
https://leetcode.com/problems/permutations/discuss/18436/Java-Clean-Code-Two-recursive-solutions
Read full article from LeetCode - Permutations | Darren's Blog
at
Labels: , , , , , , , , , ,

Labels

LeetCode (1432) GeeksforGeeks (1122) LeetCode - Review (1067) Review (882) Algorithm (668) to-do (609) Classic Algorithm (270) Google Interview (237) Classic Interview (222) Dynamic Programming (220) DP (186) Bit Algorithms (145) POJ (141) Math (137) Tree (132) LeetCode - Phone (129) EPI (122) Cracking Coding Interview (119) DFS (115) Difficult Algorithm (115) Lintcode (115) Different Solutions (110) Smart Algorithm (104) Binary Search (96) BFS (91) HackerRank (90) Binary Tree (86) Hard (79) Two Pointers (78) Stack (76) Company-Facebook (75) BST (72) Graph Algorithm (72) Time Complexity (69) Greedy Algorithm (68) Interval (63) Company - Google (62) Geometry Algorithm (61) Interview Corner (61) LeetCode - Extended (61) Union-Find (60) Trie (58) Advanced Data Structure (56) List (56) Priority Queue (53) Codility (52) ComProGuide (50) LeetCode Hard (50) Matrix (50) Bisection (48) Segment Tree (48) Sliding Window (48) USACO (46) Space Optimization (45) Company-Airbnb (41) Greedy (41) Mathematical Algorithm (41) Tree - Post-Order (41) ACM-ICPC (40) Algorithm Interview (40) Data Structure Design (40) Graph (40) Backtracking (39) Data Structure (39) Jobdu (39) Random (39) Codeforces (38) Knapsack (38) LeetCode - DP (38) Recursive Algorithm (38) String Algorithm (38) TopCoder (38) Sort (37) Introduction to Algorithms (36) Pre-Sort (36) Beauty of Programming (35) Must Known (34) Binary Search Tree (33) Follow Up (33) prismoskills (33) Palindrome (32) Permutation (31) Array (30) Google Code Jam (30) HDU (30) Array O(N) (29) Logic Thinking (29) Monotonic Stack (29) Puzzles (29) Code - Detail (27) Company-Zenefits (27) Microsoft 100 - July (27) Queue (27) Binary Indexed Trees (26) TreeMap (26) to-do-must (26) 1point3acres (25) GeeksQuiz (25) Merge Sort (25) Reverse Thinking (25) hihocoder (25) Company - LinkedIn (24) Hash (24) High Frequency (24) Summary (24) Divide and Conquer (23) Proof (23) Game Theory (22) Topological Sort (22) Lintcode - Review (21) Tree - Modification (21) Algorithm Game (20) CareerCup (20) Company - Twitter (20) DFS + Review (20) DP - Relation (20) Brain Teaser (19) DP - Tree (19) Left and Right Array (19) O(N) (19) Sweep Line (19) UVA (19) DP - Bit Masking (18) LeetCode - Thinking (18) KMP (17) LeetCode - TODO (17) Probabilities (17) Simulation (17) String Search (17) Codercareer (16) Company-Uber (16) Iterator (16) Number (16) O(1) Space (16) Shortest Path (16) itint5 (16) DFS+Cache (15) Dijkstra (15) Euclidean GCD (15) Heap (15) LeetCode - Hard (15) Majority (15) Number Theory (15) Rolling Hash (15) Tree Traversal (15) Brute Force (14) Bucket Sort (14) DP - Knapsack (14) DP - Probability (14) Difficult (14) Fast Power Algorithm (14) Pattern (14) Prefix Sum (14) TreeSet (14) Algorithm Videos (13) Amazon Interview (13) Basic Algorithm (13) Codechef (13) Combination (13) Computational Geometry (13) DP - Digit (13) LCA (13) LeetCode - DFS (13) Linked List (13) Long Increasing Sequence(LIS) (13) Math-Divisible (13) Reservoir Sampling (13) mitbbs (13) Algorithm - How To (12) Company - Microsoft (12) DP - Interval (12) DP - Multiple Relation (12) DP - Relation Optimization (12) LeetCode - Classic (12) Level Order Traversal (12) Prime (12) Pruning (12) Reconstruct Tree (12) Thinking (12) X Sum (12) AOJ (11) Bit Mask (11) Company-Snapchat (11) DP - Space Optimization (11) Dequeue (11) Graph DFS (11) MinMax (11) Miscs (11) Princeton (11) Quick Sort (11) Stack - Tree (11) 尺取法 (11) 挑战程序设计竞赛 (11) Coin Change (10) DFS+Backtracking (10) Facebook Hacker Cup (10) Fast Slow Pointers (10) HackerRank Easy (10) Interval Tree (10) Limited Range (10) Matrix - Traverse (10) Monotone Queue (10) SPOJ (10) Starting Point (10) States (10) Stock (10) Theory (10) Tutorialhorizon (10) Kadane - Extended (9) Mathblog (9) Max-Min Flow (9) Maze (9) Median (9) O(32N) (9) Quick Select (9) Stack Overflow (9) System Design (9) Tree - Conversion (9) Use XOR (9) Book Notes (8) Company-Amazon (8) DFS+BFS (8) DP - States (8) Expression (8) Longest Common Subsequence(LCS) (8) One Pass (8) Quadtrees (8) Traversal Once (8) Trie - Suffix (8) 穷竭搜索 (8) Algorithm Problem List (7) All Sub (7) Catalan Number (7) Cycle (7) DP - Cases (7) Facebook Interview (7) Fibonacci Numbers (7) Flood fill (7) Game Nim (7) Graph BFS (7) HackerRank Difficult (7) Hackerearth (7) Inversion (7) Kadane’s Algorithm (7) Manacher (7) Morris Traversal (7) Multiple Data Structures (7) Normalized Key (7) O(XN) (7) Radix Sort (7) Recursion (7) Sampling (7) Suffix Array (7) Tech-Queries (7) Tree - Serialization (7) Tree DP (7) Trie - Bit (7) 蓝桥杯 (7) Algorithm - Brain Teaser (6) BFS - Priority Queue (6) BFS - Unusual (6) Classic Data Structure Impl (6) DP - 2D (6) DP - Monotone Queue (6) DP - Unusual (6) DP-Space Optimization (6) Dutch Flag (6) How To (6) Interviewstreet (6) Knapsack - MultiplePack (6) Local MinMax (6) MST (6) Minimum Spanning Tree (6) Number - Reach (6) Parentheses (6) Pre-Sum (6) Probability (6) Programming Pearls (6) Rabin-Karp (6) Reverse (6) Scan from right (6) Schedule (6) Stream (6) Subset Sum (6) TSP (6) Xpost (6) n00tc0d3r (6) reddit (6) AI (5) Abbreviation (5) Anagram (5) Art Of Programming-July (5) Assumption (5) Bellman Ford (5) Big Data (5) Code - Solid (5) Code Kata (5) Codility-lessons (5) Coding (5) Company - WMware (5) Convex Hull (5) Crazyforcode (5) DFS - Multiple (5) DFS+DP (5) DP - Multi-Dimension (5) DP-Multiple Relation (5) Eulerian Cycle (5) Graph - Unusual (5) Graph Cycle (5) Hash Strategy (5) Immutability (5) Java (5) LogN (5) Manhattan Distance (5) Matrix Chain Multiplication (5) N Queens (5) Pre-Sort: Index (5) Quick Partition (5) Quora (5) Randomized Algorithms (5) Resources (5) Robot (5) SPFA(Shortest Path Faster Algorithm) (5) Shuffle (5) Sieve of Eratosthenes (5) Strongly Connected Components (5) Subarray Sum (5) Sudoku (5) Suffix Tree (5) Swap (5) Threaded (5) Tree - Creation (5) Warshall Floyd (5) Word Search (5) jiuzhang (5)

Popular Posts