https://leetcode.com/problems/find-k-th-smallest-pair-distance/description/
Approach #2: Binary Search + Prefix Sum
Arrays.sort(nums);
int WIDTH = 2 * nums[nums.length - 1];
//multiplicity[i] = number of nums[j] == nums[i] (j < i)
int[] multiplicity = new int[nums.length];
for (int i = 1; i < nums.length; ++i) {
if (nums[i] == nums[i-1]) {
multiplicity[i] = 1 + multiplicity[i - 1];
}
}
//prefix[v] = number of values <= v
int[] prefix = new int[WIDTH];
int left = 0;
for (int i = 0; i < WIDTH; ++i) {
while (left < nums.length && nums[left] == i) left++;
prefix[i] = left;
}
int lo = 0;
int hi = nums[nums.length - 1] - nums[0];
while (lo < hi) {
int mi = (lo + hi) / 2;
int count = 0;
for (int i = 0; i < nums.length; ++i) {
count += prefix[nums[i] + mi] - prefix[nums[i]] + multiplicity[i];
}
//count = number of pairs with distance <= mi
if (count >= k) hi = mi;
else lo = mi + 1;
}
return lo;
}
Arrays.sort(nums);
int lo = 0;
int hi = nums[nums.length - 1] - nums[0];
while (lo < hi) {
int mi = (lo + hi) / 2;
int count = 0, left = 0;
for (int right = 0; right < nums.length; ++right) {
while (nums[right] - nums[left] > mi) left++;
count += right - left;
}
//count = number of pairs with distance <= mi
if (count >= k) hi = mi;
else lo = mi + 1;
}
return lo;
}
X. Heap
X. https://leetcode.com/problems/find-k-th-smallest-pair-distance/discuss/109075/Java-solution-Binary-Search
X. https://leetcode.com/problems/find-k-th-smallest-pair-distance/discuss/109094/Java-very-Easy-and-Short(15-lines-Binary-Search-and-Bucket-Sort)-solutions
Given an integer array, return the k-th smallest distance among all the pairs. The distance of a pair (A, B) is defined as the absolute difference between A and B.
Example 1:
Input: nums = [1,3,1] k = 1 Output: 0 Explanation: Here are all the pairs: (1,3) -> 2 (1,1) -> 0 (3,1) -> 2 Then the 1st smallest distance pair is (1,1), and its distance is 0.
Note:
2 <= len(nums) <= 10000.0 <= nums[i] < 1000000.1 <= k <= len(nums) * (len(nums) - 1) / 2.
X. Approach #3: Binary Search + Sliding Window
http://hehejun.blogspot.com/2017/11/leetcodefind-k-th-smallest-pair-distance.html
这道题和Find K Pairs with Smallest Sum是类似的,我们同样可以将1D转化成2D,如下图所示:
因为我们不考虑自己和自己的差值,所以我们只考虑对角线斜向上的那一半区域。这个区域的值是自下而上自左而右递增的。并且我们可以sort array并且很简单的求出最大和最小的distance,也就是说我们可以用和K Pairs一样的方法来做一道题。因为sorted的性质,我们可以看做m个长度为n的sorted list用priority queue一个一个取直到取到第k个,但是我们有类似Kth Smallest Element in Sorted Matrix的值域Binary Search的更好的方法。同样每次求出mid然后统计小于等于mid的值的数量c,如果c >= k,hi = mid; 如果c < k, lo = mid + 1。因为array的值是有规律的,我们只需要最多m + n的时间就可以求出,假设第一列有x个小于mid的数,那么第二列就一定有>= x个,我们只需要将行指针单调地向下移动即可,列指针也是单调地向右移动,所以总的时间不会超过m + n。时间复杂度T(v) = T(v / 2) + m + n,考虑m + n一般小于v, 时间复杂度O(v * log v),
int smallestDistancePair(vector<int>& nums, int k) {
sort(nums.begin(), nums.end());
int len = nums.size(), lo = INT_MAX, hi = nums[len - 1] - nums[0];
if (len < 2)return -1;
for (int i = 1; i < len; ++i)
lo = min(lo, nums[i] - nums[i - 1]);
while (lo < hi)
{
int mid = lo + (hi - lo) / 2, c = count(nums, mid);
if (c >= k)hi = mid;
else lo = mid + 1;
}
return lo;
}
private:
int count(vector<int>& nums, int k) {
int n = nums.size(), i = 0, res = 0;
for (int j = 1; j < n; ++j)
{
while (i < j && nums[j] - nums[i] > k)++i;
res += (j - i);
}
return res;
}
https://leetcode.com/articles/find-k-th-smallest-pair-distance/
http://hehejun.blogspot.com/2017/11/leetcodefind-k-th-smallest-pair-distance.html
这道题和Find K Pairs with Smallest Sum是类似的,我们同样可以将1D转化成2D,如下图所示:
因为我们不考虑自己和自己的差值,所以我们只考虑对角线斜向上的那一半区域。这个区域的值是自下而上自左而右递增的。并且我们可以sort array并且很简单的求出最大和最小的distance,也就是说我们可以用和K Pairs一样的方法来做一道题。因为sorted的性质,我们可以看做m个长度为n的sorted list用priority queue一个一个取直到取到第k个,但是我们有类似Kth Smallest Element in Sorted Matrix的值域Binary Search的更好的方法。同样每次求出mid然后统计小于等于mid的值的数量c,如果c >= k,hi = mid; 如果c < k, lo = mid + 1。因为array的值是有规律的,我们只需要最多m + n的时间就可以求出,假设第一列有x个小于mid的数,那么第二列就一定有>= x个,我们只需要将行指针单调地向下移动即可,列指针也是单调地向右移动,所以总的时间不会超过m + n。时间复杂度T(v) = T(v / 2) + m + n,考虑m + n一般小于v, 时间复杂度O(v * log v),
int smallestDistancePair(vector<int>& nums, int k) {
sort(nums.begin(), nums.end());
int len = nums.size(), lo = INT_MAX, hi = nums[len - 1] - nums[0];
if (len < 2)return -1;
for (int i = 1; i < len; ++i)
lo = min(lo, nums[i] - nums[i - 1]);
while (lo < hi)
{
int mid = lo + (hi - lo) / 2, c = count(nums, mid);
if (c >= k)hi = mid;
else lo = mid + 1;
}
return lo;
}
private:
int count(vector<int>& nums, int k) {
int n = nums.size(), i = 0, res = 0;
for (int j = 1; j < n; ++j)
{
while (i < j && nums[j] - nums[i] > k)++i;
res += (j - i);
}
return res;
}
https://leetcode.com/articles/find-k-th-smallest-pair-distance/
We will use a sliding window approach to count the number of pairs with distance
<= guess.
For every possible
Time Complexity: , where is the length of right, we maintain the loop invariant: left is the smallest value such that nums[right] - nums[left] <= guess. Then, the number of pairs with right as it's right-most endpoint is right - left, and we add all of these up.nums, and is equal to nums[nums.length - 1] - nums[0]. The factor comes from our binary search, and we do work inside our call to possible (or to calculate count in Java). The final factor comes from sorting.
public int smallestDistancePair(int[] nums, int k) {
Arrays.sort(nums);
int lo = 0;
int hi = nums[nums.length - 1] - nums[0];
while (lo < hi) {
int mi = (lo + hi) / 2;
int count = 0, left = 0;
for (int right = 0; right < nums.length; ++right) {
while (nums[right] - nums[left] > mi)
left++;
count += right - left;
}
// count = number of pairs with distance <= mi
if (count >= k)
hi = mi;
else
lo = mi + 1;
}
return lo;
}
https://leetcode.com/problems/find-k-th-smallest-pair-distance/discuss/109082/Approach-the-problem-using-the-%22trial-and-error%22-algorithm
Well, normally we would refrain from using the naive trial and error algorithm for solving problems since it generally leads to bad time performance. However, there are situations where this naive algorithm may outperform other more sophisticated solutions, and LeetCode does have a few such problems (listed at the end of this post -- ironically most of them are "hard" problems). So I figure it might be a good idea to bring it up and describe a general procedure for applying this algorithm.
The basic idea for the trial and error algorithm is actually very simple and summarized below:
Step 1: Construct a candidate solution.Step 2: Verify if it meets our requirements.Step 3: If it does, accept the solution; else discard it and repeat from Step 1.
However, to make this algorithm work efficiently, the following two conditions need to be true:
Condition 1: We have an efficient verification algorithm in
Condition 2: The search space formed by all candidate solutions is small or we have efficient ways to traverse (or search) this space if it is large.
Step 2;Condition 2: The search space formed by all candidate solutions is small or we have efficient ways to traverse (or search) this space if it is large.
The first condition ensures that each verification operation can be done quickly while the second condition limits the total number of such operations that need to be done. The two combined will guarantee that we have an efficient trial and error algorithm (which also means if any of them cannot be satisfied, you should probably not even consider this algorithm).
Now let's look at this problem:
719. Find The K-th Smallest Pair Distance, and see how we can apply the trial and error algorithm.I -- Construct a candidate solution
To construct a candidate solution, we need to understand first what the desired solution is. The problem description requires we output the
K-th smallest pair distance, which is nothing more than a non-negative integer (since the input array nums is an integer array and pair distances are absolute values). Therefore our candidate solution should also be a non-negative integer.II -- Search space formed by all the candidate solutions
Let
min and max be the minimum and maximum numbers in the input array nums, and d = max - min, then any pair distance from nums must lie in the range [0, d]. As such, our desired solution is also within this range, which implies the search space will be [0, d] (any number outside this range can be ruled out immediately without further verification).III -- Verify a given candidate solution
This is the key part of this trial and error algorithm. So given a candidate integer, how do we determine if it is the
K-th smallest pair distance?
First, what does the
K-th smallest pair distance really mean? By definition, if we compute all the pair distances and sort them in ascending order, then the K-thsmallest pair distance will be the one at index K - 1. This is essentially the naive way for solving this problem (but will be rejected due to MLE, as expected).
Apparently the above definition cannot be used to do the verification, as it requires explicit computation of the pair distance array. Fortunately there is another way to define the
K-th smallest pair distance: given an integer num, let count(num) denote the number of pair distances that are no greater than num, then the K-thsmallest pair distance will be the smallest integer such that count(num) >= K.
Here is a quick justification of the alternative definition. Let
num_k be the K-th pair distance in the sorted pair distance array with index K - 1, as specified in the first definition. Since all the pair distances up to index K - 1 are no greater than num_k, we have count(num_k) >= K. Now suppose num is the smallest integer such that count(num) >= K, we show num must be equal to num_k as follows:- If
num_k < num, sincecount(num_k) >= K, thennumwill not be the smallest integer such thatcount(num) >= K, which contradicts our assumption. - If
num_k > num, sincecount(num) >= K, by definition of thecountfunction, there are at leastKpair distances that are no greater thannum, which implies there are at leastKpair distances that are smaller thannum_k. This meansnum_kcannot be theK-thpair distance, contradicting our assumption again.
Taking advantage of this alternative definition of the
K-th smallest pair distance, we can transform the verification process into a counting process. So how exactly do we do the counting?IV -- Count the number of pair distances no greater than the given integer
As I mentioned, we cannot use the pair distance arrays, which means the only option is the input array itself. If there is no order among its elements, we got no better way other than compute and test each pair distance one by one. This leads to a
O(n^2) verification algorithm, which is as bad as, if not worse than, the aforementioned naive solution. So we need to impose some order to nums, which by default means sorting.
Now suppose
nums is sorted in ascending order, how do we proceed with the counting for a given number num? Note that each pair distance d_ij is characterized by a pair of indices (i, j) with i < j, that is d_ij = nums[j] - nums[i]. If we keep the first index i fixed, then d_ij <= num is equivalent to nums[j] <= nums[i] + num. This suggests that at least we can do a binary search to find the smallest index j such that nums[j] > nums[i] + num for each index i, then the count from index i will be j - i - 1, and in total we have an O(nlogn) verification algorithm.
It turns out the counting can be done in linear time using the classic two-pointer technique if we make use of the following property: assume we have two starting indices
i1 and i2 with i1 < i2, let j1 and j2 be the smallest index such that nums[j1] > nums[i1] + num and nums[j2] > nums[i2] + num, respectively, then it must be true that j2 >= j1. The proof is straightforward: suppose j2 < j1, since j1is the smallest index such that nums[j1] > nums[i1] + num, we should have nums[j2] <= nums[i1] + num. On the other hand, nums[j2] > nums[i2] + num >= nums[i1] + num. The two inequalities contradict each other, thus validate our conclusion above.V -- How to traverse (or search) the search space efficiently
Up to this point, we know the search space, know how to construct the candidate solution and how to verify it by counting, we still need one last piece for the puzzle: how to traverse the search space.
Of course we can do the naive linear walk by trying each integer from
0 up to d and choose the first integer num such that count(num) >= K. The time complexity will be O(nd). However, given that d can be much larger than n, this algorithm can be much worse than the naive O(n^2) solution mentioned before.
The key observation here is that the candidate solutions are sorted naturally in ascending order, so a binary search is possible. Another fact is the non-decreasing property of the
count function: give two integers num1 and num2 such that num1 < num2, then count(num1) <= count(num2) (I will leave the verification to you). So a binary walk of the search space will look like this:- Let
[l, r]be the current search space, and initializel = 0,r = d. - If
l < r, compute the middle pointm = (l + r) / 2and evaluatecount(m). - If
count(m) < K, we throw away the left half of current search space and setl = m + 1; else ifcount(m) >= Kwe throw away the right half and setr = m.
You probably will wonder why we throw away the right half of the search space even if
count(m) == K. Note that the K-th smallest pair distance num_k is the minimum integer such that count(num_k) >= K. If count(m) == K, then we know num_k <= m (but not num_k == m, think about it!) so it makes no sense keeping the right half.VI -- Putting everything together, aka, solutions
Don't get scared by the above analyses. The final solution is much simpler to write once you understand it. Here is the Java program for the trial and error algorithm. The time complexity is
O(nlogd + nlogn) (don't forget the sorting) and space complexity is O(1).public int smallestDistancePair(int[] nums, int k) {
Arrays.sort(nums);
int n = nums.length;
int l = 0;
int r = nums[n - 1] - nums[0];
for (int cnt = 0; l < r; cnt = 0) {
int m = l + (r - l) / 2;
for (int i = 0, j = 0; i < n; i++) {
while (j < n && nums[j] <= nums[i] + m) j++;
cnt += j - i - 1;
}
if (cnt < k) {
l = m + 1;
} else {
r = m;
}
}
return l;
}
Lastly here is a list of LeetCode problems that can be solved using the trial and error algorithm (you're welcome to add more examples):
Anyway, this post is just a reminder to you that the trial and error algorithm is worth trying if you find all other common solutions suffer severely from bad time or space performance. Also it's always recommended to perform a quick evaluation of the search space size and potential verification algorithm to estimate the complexity before you are fully committed to this algorithm
Let's binary search for the answer. It's definitely in the range
[0, W], where W = max(nums) - min(nums)].
Let
possible(guess) be true if and only if there are k or more pairs with distance less than or equal to guess. We will focus on evaluating our possible function quickly.
Algorithm
Let
prefix[v] be the number of points in nums less than or equal to v. Also, let multiplicity[j] be the number of points i with i < j and nums[i] == nums[j]. We can record both of these with a simple linear scan.
Now, for every point
i, the number of points j with i < j and nums[j] - nums[i] <= guess is prefix[x+guess] - prefix[x] + (count[i] - multiplicity[i]), where count[i] is the number of ocurrences of nums[i] in nums. The sum of this over all i is the number of pairs with distance <= guess.
Finally, because the sum of
count[i] - multiplicity[i] is the same as the sum of multiplicity[i], we could just replace that term with multiplicity[i] without affecting the answer. (Actually, the sum of multiplicities in total will be a constant used in the answer, so we could precalculate it if we wanted.)
In our Java solution, we computed
possible = count >= k directly in the binary search instead of using a helper function.- Time Complexity: , where is the length of
nums, and is equal tonums[nums.length - 1] - nums[0]. We do work to calculateprefixinitially. The factor comes from our binary search, and we do work inside our call topossible(or to calculatecountin Java). The final factor comes from sorting. - Space Complexity: , the space used to store
multiplicityandprefix.
Arrays.sort(nums);
int WIDTH = 2 * nums[nums.length - 1];
//multiplicity[i] = number of nums[j] == nums[i] (j < i)
int[] multiplicity = new int[nums.length];
for (int i = 1; i < nums.length; ++i) {
if (nums[i] == nums[i-1]) {
multiplicity[i] = 1 + multiplicity[i - 1];
}
}
//prefix[v] = number of values <= v
int[] prefix = new int[WIDTH];
int left = 0;
for (int i = 0; i < WIDTH; ++i) {
while (left < nums.length && nums[left] == i) left++;
prefix[i] = left;
}
int lo = 0;
int hi = nums[nums.length - 1] - nums[0];
while (lo < hi) {
int mi = (lo + hi) / 2;
int count = 0;
for (int i = 0; i < nums.length; ++i) {
count += prefix[nums[i] + mi] - prefix[nums[i]] + multiplicity[i];
}
//count = number of pairs with distance <= mi
if (count >= k) hi = mi;
else lo = mi + 1;
}
return lo;
}
As in Approach #2, let's binary search for the answer, and we will focus on evaluating our
possible function quickly.
Algorithm
We will use a sliding window approach to count the number of pairs with distance
<= guess.
For every possible
right, we maintain the loop invariant: left is the smallest value such that nums[right] - nums[left] <= guess. Then, the number of pairs with right as it's right-most endpoint is right - left, and we add all of these up.- Time Complexity: , where is the length of
nums, and is equal tonums[nums.length - 1] - nums[0]. The factor comes from our binary search, and we do work inside our call topossible(or to calculatecountin Java). The final factor comes from sorting. - Space Complexity: . No additional space is used except for integer variables.
Arrays.sort(nums);
int lo = 0;
int hi = nums[nums.length - 1] - nums[0];
while (lo < hi) {
int mi = (lo + hi) / 2;
int count = 0, left = 0;
for (int right = 0; right < nums.length; ++right) {
while (nums[right] - nums[left] > mi) left++;
count += right - left;
}
//count = number of pairs with distance <= mi
if (count >= k) hi = mi;
else lo = mi + 1;
}
return lo;
}
X. Heap
Sort the points. For every point with index
i, the pairs with indexes (i, j) [by order of distance] are (i, i+1), (i, i+2), ..., (i, N-1).
Let's keep a heap of pairs, initially
heap = [(i, i+1) for all i], and ordered by distance (the distance of (i, j) is nums[j] - nums[i].) Whenever we use a pair (i, x) from our heap, we will add (i, x+1) to our heap when appropriate.- Time Complexity: , where is the length of
nums. As , this is in the worst case. The complexity added by our heap operations is either in the Java solution, or in the Python solution because theheapq.heapifyoperation is linear time. Additionally, we add complexity due to sorting. - Space Complexity: , the space used to store our
heapof at mostN-1element
public int smallestDistancePair(int[] nums, int k) {
Arrays.sort(nums);
PriorityQueue<Node> heap = new PriorityQueue<Node>(nums.length,
Comparator.<Node>comparingInt(node -> nums[node.nei] - nums[node.root]));
for (int i = 0; i + 1 < nums.length; ++i) {
heap.offer(new Node(i, i + 1));
}
Node node = null;
for (; k > 0; --k) {
node = heap.poll();
if (node.nei + 1 < nums.length) {
heap.offer(new Node(node.root, node.nei + 1));
}
}
return nums[node.nei] - nums[node.root];
}
class Node {
int root;
int nei;
Node(int r, int n) {
root = r;
nei = n;
}
}
X. https://leetcode.com/problems/find-k-th-smallest-pair-distance/discuss/109075/Java-solution-Binary-Search
// Returns number of pairs with absolute difference less than or equal to mid.
private int countPairs(int[] a, int mid) {
int n = a.length, res = 0;
for (int i = 0; i < n; ++i) {
int j = i;
while (j < n && a[j] - a[i] <= mid) j++;
res += j - i - 1;
}
return res;
}
public int smallestDistancePair(int a[], int k) {
int n = a.length;
Arrays.sort(a);
// Minimum absolute difference
int low = a[1] - a[0];
for (int i = 1; i < n - 1; i++)
low = Math.min(low, a[i + 1] - a[i]);
// Maximum absolute difference
int high = a[n - 1] - a[0];
// Do binary search for k-th absolute difference
while (low < high) {
int mid = low + (high - low) / 2;
if (countPairs(a, mid) < k)
low = mid + 1;
else
high = mid;
}
return low;
}
Improved countPairs to use binary search too:
// Returns index of first index of element which is greater than key
private int upperBound(int[] a, int low, int high, int key) {
if (a[high] <= key) return high + 1;
while (low < high) {
int mid = low + (high - low) / 2;
if (key >= a[mid]) {
low = mid + 1;
} else {
high = mid;
}
}
return low;
}
// Returns number of pairs with absolute difference less than or equal to mid.
private int countPairs(int[] a, int mid) {
int n = a.length, res = 0;
for (int i = 0; i < n; i++) {
res += upperBound(a, i, n - 1, a[i] + mid) - i - 1;
}
return res;
}
public int smallestDistancePair(int a[], int k) {
int n = a.length;
Arrays.sort(a);
// Minimum absolute difference
int low = a[1] - a[0];
for (int i = 1; i < n - 1; i++)
low = Math.min(low, a[i + 1] - a[i]);
// Maximum absolute difference
int high = a[n - 1] - a[0];
// Do binary search for k-th absolute difference
while (low < high) {
int mid = low + (high - low) / 2;
if (countPairs(a, mid) < k)
low = mid + 1;
else
high = mid;
}
return low;
}X. https://leetcode.com/problems/find-k-th-smallest-pair-distance/discuss/109094/Java-very-Easy-and-Short(15-lines-Binary-Search-and-Bucket-Sort)-solutions
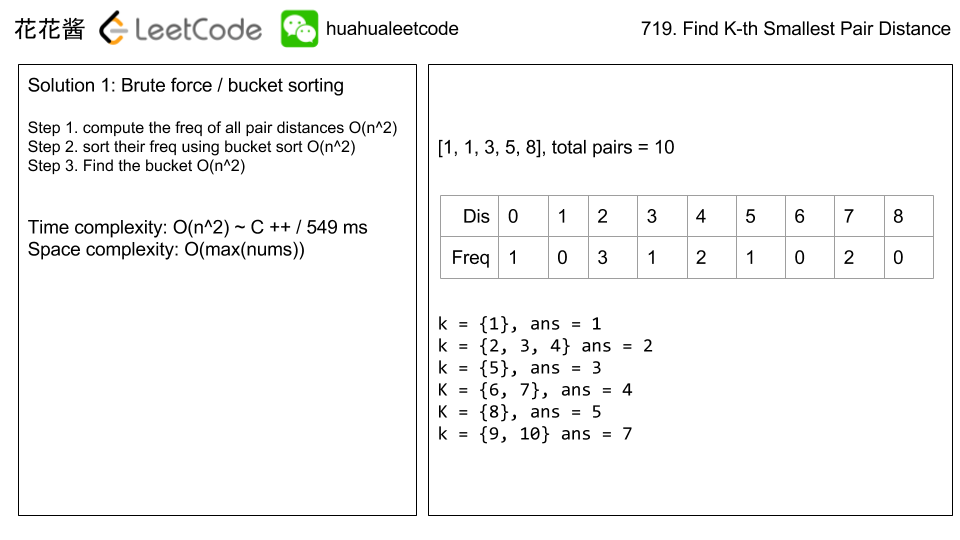
Bucket Sort Solution: O(N^2)
public int smallestDistancePair(int[] nums, int k) {
int len=nums.length;
int len2=1000000;
int[] dp= new int[len2];
for(int i=1;i<len;i++){
for(int j=0;j<i;j++){
int dif= Math.abs(nums[i]-nums[j]);
dp[dif]++;
}
}
int sum=0;
for(int i=0;i<len2;i++){
sum+=dp[i];
if(sum>=k) return i;
}
return 0;
}