LeetCode 731 - My Calendar II

Related: LeetCode 729 - My Calendar I
LeetCode 731 - My Calendar II
LeetCode 732 - My Calendar III
https://leetcode.com/problems/my-calendar-ii/description/

Implement a MyCalendarTwo class to store your events. A new event can be added if adding the event will not cause a triple booking.

Your class will have one method, book(int start, int end). Formally, this represents a booking on the half open interval [start, end), the range of real numbers x such that start <= x < end.

A triple booking happens when three events have some non-empty intersection (ie., there is some time that is common to all 3 events.)

For each call to the method MyCalendar.book, return true if the event can be added to the calendar successfully without causing a triple booking. Otherwise, return false and do not add the event to the calendar.

Your class will be called like this: MyCalendar cal = new MyCalendar(); MyCalendar.book(start, end)

Example 1:

MyCalendar();
MyCalendar.book(10, 20); // returns true
MyCalendar.book(50, 60); // returns true
MyCalendar.book(10, 40); // returns true
MyCalendar.book(5, 15); // returns false
MyCalendar.book(5, 10); // returns true
MyCalendar.book(25, 55); // returns true
Explanation: 
The first two events can be booked.  The third event can be double booked.
The fourth event (5, 15) can't be booked, because it would result in a triple booking.
The fifth event (5, 10) can be booked, as it does not use time 10 which is already double booked.
The sixth event (25, 55) can be booked, as the time in [25, 40) will be double booked with the third event;
the time [40, 50) will be single booked, and the time [50, 55) will be double booked with the second event.

Note:

The number of calls to MyCalendar.book per test case will be at most 1000.

In calls to MyCalendar.book(start, end), start and end are integers in the range [0, 10^9].

X. https://leetcode.com/problems/my-calendar-ii/discuss/109528/nlogd-Java-solution-using-segment-tree-with-lazy-propagation-applicable-to-the-general-case-of-K-booking
nlogd Java solution using segment tree with lazy propagation -- applicable to the general case of K-booking

Step I -- Define the segment tree node

A segment tree node typically contains four pieces of information:

1. The segment this tree node represents: [l, r] (both inclusive)
2. The property fields associated with this segment: for this problem, this will be the maximum integer k such that there exists a k-booking within the segment [l, r].
3. The lazy fields corresponding to each property field above: this is required for efficient range updating, and can be dropped if there is no range updating (see this article and this Quora post for more detailed explanation).
4. The pointer to the left and right subtrees: left and right.

Here is what our segment tree node looks like:

private static class SegmentTreeNode {
    int l, r;
    int k, lazy;
    SegmentTreeNode left, right;
        
    SegmentTreeNode(int l, int r, int k) {
        this.l = l;
        this.r = r;
        this.k = k;
        this.lazy = 0;
        this.left = this.right = null;
    }
}

---

Step II -- Write the query and update functions

Given a range [i, j], corresponding to an event of range [i, j+1), the query function should return the maximum integer k such that there exists a k-booking within the range [i, j], so that we can use the information to determine whether this event can be booked or not.

If this event can be booked, the update function then will update all segments within the range [i, j] accordingly (in this case, increase the k value of all segments within the range [i, j] by 1).

A. -- The general structure of the query function:

1. Normalize the segment tree node -- the node may have been marked lazy from previous steps, so we need to remove the laziness in order to see the most recent values.
2. Check if the query range is invalid or out of range with respect to current segment -- if so, simply return 0.
3. Check if the query range covers current segment -- if so, simply return the k value of current segment node.
4. Recurse to the left and right subtrees -- simply call the query function on the two child nodes of current segment node with the same query range [i, j].
5. Return the combined results of the left and right subtrees -- in this case, it will be the larger one of the two, since we need the maximum integer k.

Here is what it looks like:

private int query(SegmentTreeNode node, int i, int j) {
    normalize(node);
    
    if (i > j || node == null || i > node.r || j < node.l) return 0;
    
    if (i <= node.l && node.r <= j) return node.k;
        
    return Math.max(query(node.left, i, j), query(node.right, i, j));
}

B. -- The general structure of the update function (very similar to query):

1. Normalize the segment tree node -- the node may have been marked lazy from previous steps, so we need to remove the laziness in order to avoid overwriting prior updates.
2. Check if the query range is invalid or out of range with respect to current segment -- if so, simply return.
3. Check if the query range covers current segment -- if so, update current segment node and mark its child nodes as lazy, then return.
4. Recurse to the left and right subtrees -- simply call the update function on the two child nodes of current segment node with the same query range [i, j].
5. Propagate the results of the left and right subtrees back to the parent node -- in this case, the k value of the parent node will be set to the larger one of the two subtree nodes.

Here is what it looks like:

private void update(SegmentTreeNode node, int i, int j, int val) {
    normalize(node);
        
    if (i > j || node == null || i > node.r || j < node.l) return;
    
    if (i <= node.l && node.r <= j) {
        node.lazy = val;
        normalize(node);
        return;
    }
        
    update(node.left, i, j, val);
    update(node.right, i, j, val);
    
    node.k = Math.max(node.left.k, node.right.k);
}

C. -- The general structure of the normalize function:

1. Update current segment node if it is marked lazy -- in this case, a node is considered lazy if its lazy field is greater than 0, and the updating is done by adding the lazy field to the k field.
2. Push the laziness down to the child nodes -- first make sure current segment node is not a leaf node (a leaf node has l == r), then depending on whether the two child nodes are null or not, we either initialize them with the updated value of current node or simply mark their lazy field (this is done by adding the lazy field of current node to those of its child nodes).
3. Reset the laziness of current segment node so as to normalize it -- in this case, we reset the lazy field to 0.

Here is what it looks like:

private void normalize(SegmentTreeNode node) {
    if (node.lazy > 0) node.k += node.lazy;
    
    if (node.l < node.r) {
        if (node.left == null || node.right == null) {
            int m = node.l + (node.r - node.l) / 2;
            node.left = new SegmentTreeNode(node.l, m, node.k);
            node.right = new SegmentTreeNode(m + 1, node.r, node.k);
        
        } else if (node.lazy > 0) {
            node.left.lazy += node.lazy;
            node.right.lazy += node.lazy;
        }
    }
    
    node.lazy = 0;
}

---

Step III -- Initialize the root node and write the book function

The root node should at least cover the maximum range allowed for all events, which for this problem is [0, 10^9]. Its k value will be set to 0 since at the beginning no events are booked.

The book function will first query the k value within the range of the event to be added. If k >= 2, then there exists at least one double booking within that range, and adding the event would cause a triple booking, therefore the event will be dropped and the function return false. Otherwise, it will add the event to the calendar by updating accordingly the segments within the range of the added event and return true.

Here is the root node and the book function:

SegmentTreeNode root;

public MyCalendarTwo() {
    root = new SegmentTreeNode(0, 1_000_000_000, 0);
}

public boolean book(int start, int end) {
    int k = query(root, start, end - 1);
    if (k >= 2) return false;  // For the general case of `K`-booking, replace `2` with `K-1`
    
    update(root, start, end - 1, 1);
    return true;
}

---

Step IV -- complexity analyses

Time complexity: for each call of the function book, we need to do at most one query and one update, both of which can be done in logd time, where d is the maximum range allowed for all events (in this case d = 10^9). Therefore, for n calls of the book function, the total time complexity will be O(nlogd).

Space complexity: in the worst case, the segment tree can be a full binary tree with 2d nodes. However, this is very unlikely as it would require a total of d calls of the book function, each with an event of range 1. For n calls of the book function, the average space cost is roughly O(nlogd).

---

Step V -- Generalization to arbitrary K-booking

The generalization to K-booking is trivial. The only modification we need to do is to replace the number to which we compare the k value in the book function to K-1. Everything else will remain the same.

For "My Calendar I", this number is 1; for "My Calendar II", this number is 2. For "My Calendar III", however, the events can always be added to the calendar so we don't even need the query function. The maximum value of K such that there exists a K-booking in the calendar is given, by definition, the k field of the root node after updating.

---

Lastly, for you convenience, here is the complete solution for "My Calendar II" by putting everything together:

private static class SegmentTreeNode {
    int l, r;
    int k, lazy;
    SegmentTreeNode left, right;
        
    SegmentTreeNode(int l, int r, int k) {
        this.l = l;
        this.r = r;
        this.k = k;
        this.lazy = 0;
        this.left = this.right = null;
    }
}

private int query(SegmentTreeNode node, int i, int j) {
    normalize(node);
    
    if (i > j || node == null || i > node.r || j < node.l) return 0;
    
    if (i <= node.l && node.r <= j) return node.k;
        
    return Math.max(query(node.left, i, j), query(node.right, i, j));
}

private void update(SegmentTreeNode node, int i, int j, int val) {
    normalize(node);
        
    if (i > j || node == null || i > node.r || j < node.l) return;
    
    if (i <= node.l && node.r <= j) {
        node.lazy = val;
        normalize(node);
        return;
    }
        
    update(node.left, i, j, val);
    update(node.right, i, j, val);
    
    node.k = Math.max(node.left.k, node.right.k);
}

private void normalize(SegmentTreeNode node) {
    if (node.lazy > 0) node.k += node.lazy;
    
    if (node.l < node.r) {
        if (node.left == null || node.right == null) {
            int m = node.l + (node.r - node.l) / 2;
            node.left = new SegmentTreeNode(node.l, m, node.k);
            node.right = new SegmentTreeNode(m + 1, node.r, node.k);
        
        } else if (node.lazy > 0) {
            node.left.lazy += node.lazy;
            node.right.lazy += node.lazy;
        }
    }
    
    node.lazy = 0;
}


SegmentTreeNode root;

public MyCalendarTwo() {
    root = new SegmentTreeNode(0, 1_000_000_000, 0);
}

public boolean book(int start, int end) {
    int k = query(root, start, end - 1);
    if (k >= 2) return false;
    
    update(root, start, end - 1, 1);
    return true;
}

X. Brute Force
https://klein-hu.github.io/algorithm/2018/12/03/LeetCode-731-My-Calendar-II.html

Maintain a list of bookings and a list of double bookings. When booking a new event [start, end), if it conflicts with a double booking, it will have a triple booking and be invalid. Otherwise, parts that overlap the calendar will be a double booking.

Evidently, two events [s1, e1) and [s2, e2) do not conflict if and only if one of them starts after the other one ends: either e1 <= s2 OR e2 <= s1. By De Morgan's laws, this means the events conflict when s1 < e2 AND s2 < e1.

If our event conflicts with a double booking, it's invalid. Otherwise, we add conflicts with the calendar to our double bookings, and add the event to our calendar.

• Time Complexity: $O(N^2)$, where $N$ is the number of events booked. For each new event, we process every previous event to decide whether the new event can be booked. This leads to $\sum_k^N O(k) = O(N^2)$complexity.
• Space Complexity: $O(N)$, the size of the calendar.

https://leetcode.com/problems/my-calendar-ii/discuss/109520/Java-O(n)-time-solution
https://leetcode.com/problems/my-calendar-ii/discuss/109530/N2-Python-Short-and-Elegant

We store an array self.overlaps of intervals that are double booked, and self.calendar for intervals which have been single booked. We use the line start < j and end > i to check if the ranges [start, end) and [i, j) overlap.

The clever idea is we do not need to "clean up" ranges in calendar: if we have [1, 3] and [2, 4], this will be calendar = [[1,3],[2,4]] and overlaps = [[2,3]]. We don't need to spend time transforming the calendar to calendar = [[1,4]].

    List<int[]> calendar;
    List<int[]> overlaps;

    MyCalendarTwo() {
        calendar = new ArrayList();
    }

    public boolean book(int start, int end) {
        for (int[] iv: overlaps) {
            if (iv[0] < end && start < iv[1]) return false;
        }
        for (int[] iv: calendar) {
            if (iv[0] < end && start < iv[1])
                overlaps.add(new int[]{Math.max(start, iv[0]), Math.min(end, iv[1])});
        }
        calendar.add(new int[]{start, end});
        return true;
    }
https://leetcode.com/problems/my-calendar-ii/discuss/109519/JavaC++-Clean-Code-with-Explanation
https://leetcode.com/problems/my-calendar-ii/discuss/109555/Java-solution-TreeMap-+-List

http://bookshadow.com/weblog/2017/11/20/leetcode-my-calendar-ii/
private Map<Double, Integer> dmap; private List<int[]> events; public MyCalendarTwo() { dmap = new HashMap<>(); events = new ArrayList<>(); } public boolean book(int start, int end) { int cs = 1, ce = 1; for (int[] e: events) { if (e[0] <= start && start < e[1]) cs++; if (e[0] < end && end < e[1]) ce++; } if (cs > 2 || ce > 2) return false; List<Double> addList = new ArrayList<>(); for (double key : dmap.keySet()) { if (start <= key && key <= end - 0.5) { if (dmap.get(key) == 2) return false; addList.add(key); } } for (Double key: addList) dmap.put(key, dmap.get(key) + 1); if (!dmap.containsKey(start)) { dmap.put((double)start, cs); } if (!dmap.containsKey(end - 0.5)) { dmap.put(end - 0.5, ce); } events.add(new int[]{start, end}); return true; }

X. Boundary Count
Time Complexity: O(n^2logn)

http://www.cnblogs.com/grandyang/p/7968035.html

下面这种方法相当的巧妙，我们建立一个时间点和次数之间的映射，规定遇到起始时间点，次数加1，遇到结束时间点，次数减1。那么我们首先更改新的起始时间start和结束时间end的映射，start对应值增1，end对应值减1。然后定义一个变量cnt，来统计当前的次数。我们使用treemap具有自动排序的功能，所以我们遍历的时候就是按时间顺序的，最先遍历到的一定是一个起始时间，所以加上其映射值，一定是个正数。那么我们想，如果此时只有一个区间，就是刚加进来的区间的话，那么首先肯定遍历到start，那么cnt此时加1，然后就会遍历到end，那么此时cnt减1，最后下来cnt为0，没有重叠。还是用具体数字来说吧，我们现在假设treemap中已经加入了一个区间[3, 5)了，那么我们就有下面的映射：

3 -> 1

5 -> -1

假如我们此时要加入的区间为[6, 8)的话，那么在遍历到6的时候，前面经过3和5，分别加1减1，那么cnt又重置为0了，而后面的6和8也是分别加1减1，还是0。那么加入我们新加入的区间为[3, 8]时，那么此时的映射为：

3 -> 2

5 -> -1

8 -> -1

那么我们最先遍历到3，cnt为2，没有超过3，我们知道此时有两个事件有重叠，是允许的。然后遍历5和8，分别减去1，最终又变成0了，始终cnt没有超过2，所以是符合题意的。如果此时我们再加入一个新的区间[1, 4)，那么此时的映射为：

1 -> 1

3 -> 2

4 -> -1

5 -> -1

8 -> -1

那么我们先遍历到1，cnt为1，然后遍历到3，此时cnt为3了，那么我们就知道有三个事件有重叠区间了，所以这个新区间是不能加入的，那么我们要还原其start和end做的操作，把start的映射值减1，end的映射值加1，然后返回false。否则没有三个事件有共同重叠区间的话，返回true即可

    bool book(int start, int end) {
        ++freq[start];
        --freq[end];
        int cnt = 0;
        for (auto f : freq) {
            cnt += f.second;
            if (cnt == 3) {
                --freq[start];
                ++freq[end];
                return false;
            }
        }
        return true;
    }

private:
    map<int, int> freq;

https://leetcode.com/problems/my-calendar-ii/discuss/109522/Simplified-winner's-solution

Note we must use TreeMap because order matters

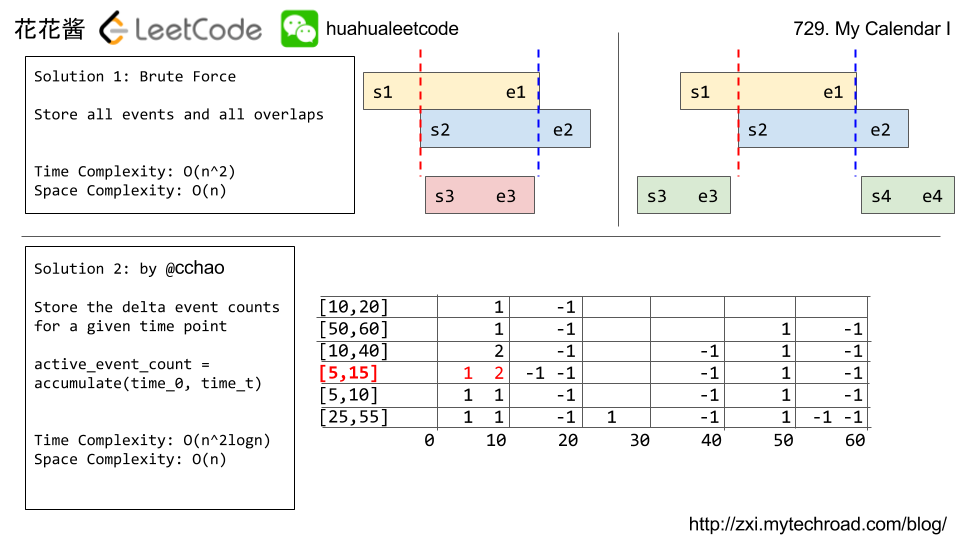
For each time point, store how the number of booked events changes. For each booking attempt, book it and undo the booking if it causes a triple booking (as determined by going through the time line, keeping track of the number of booked events).

When booking a new event [start, end), count delta[start]++ and delta[end]--. When processing the values of delta in sorted order of their keys, the running sum active is the number of events open at that time. If the sum is 3 or more, that time is (at least) triple booked.

• Time Complexity: $O(N^2)$, where $N$ is the number of events booked. For each new event, we traverse delta in $O(N)$ time.
• Space Complexity: $O(N)$, the size of delta.

shouldn't the time complexity of solution 2 be O(N^2logN)?
Since for every book(), it's N for the for loop and logN for the TreeMap insert?
Thus for every book(), it's O(NlogN), then you call book() N times, so O(N^2logN)?

    TreeMap<Integer, Integer> delta;

    public MyCalendarTwo() {
        delta = new TreeMap();
    }

    public boolean book(int start, int end) {
        delta.put(start, delta.getOrDefault(start, 0) + 1);
        delta.put(end, delta.getOrDefault(end, 0) - 1);

        int active = 0;
        for (int d: delta.values()) {
            active += d;
            if (active >= 3) {
                delta.put(start, delta.get(start) - 1);
                delta.put(end, delta.get(end) + 1);
                if (delta.get(start) == 0)
                    delta.remove(start);
                return false;
            }
        }
        return true;
    }

Time Complexity: O(n^2logn)
https://zxi.mytechroad.com/blog/tag/sweep-line/

    bool book(int start, int end) {

        ++delta_[start];

        --delta_[end];

        int count = 0;

        for (const auto& kv : delta_) {

            count += kv.second;

            if (count == 3) {

                --delta_[start];

                ++delta_[end];

                return false;

            }

            if (kv.first > end) break;

        }

        return true;

    }

private:

    map<int, int> delta_;

https://leetcode.com/problems/my-calendar-ii/discuss/109550/Simple-AC-by-TreeMap
用当前状态表示是否可以book， 跟leetcode 838 多米诺那道题解法很接近

    private TreeMap<Integer, Integer> map;    
    
    public MyCalendarTwo() {
        map = new TreeMap<>();
    }
    
    public boolean book(int start, int end) {
        map.put(start, map.getOrDefault(start, 0) + 1);
        map.put(end, map.getOrDefault(end, 0) - 1);
        int count = 0;
        for(Map.Entry<Integer, Integer> entry : map.entrySet()) {
            count += entry.getValue();
            if(count > 2) {
                map.put(start, map.get(start) - 1);
                if(map.get(start) == 0) {
                    map.remove(start);
                }
                map.put(end, map.get(end) + 1);
                if(map.get(end) == 0) {
                    map.remove(end);
                }
                return false;
            }
        }
        return true;
    }

http://bookshadow.com/weblog/2017/11/20/leetcode-my-calendar-ii/

利用HashMap存储各区间端点被覆盖的次数，记为dmap

利用List存储所有不triple booking的活动，记为events

每次添加活动时，遍历events，判断当前活动与已存在活动是否发生冲突，并更新dmap

将终点坐标减去0.5，与起点坐标做区分

private Map<Double, Integer> dmap; private List<int[]> events; public MyCalendarTwo() { dmap = new HashMap<>(); events = new ArrayList<>(); } public boolean book(int start, int end) { int cs = 1, ce = 1; for (int[] e: events) { if (e[0] <= start && start < e[1]) cs++; if (e[0] < end && end < e[1]) ce++; } if (cs > 2 || ce > 2) return false; List<Double> addList = new ArrayList<>(); for (double key : dmap.keySet()) { if (start <= key && key <= end - 0.5) { if (dmap.get(key) == 2) return false; addList.add(key); } } for (Double key: addList) dmap.put(key, dmap.get(key) + 1); if (!dmap.containsKey(start)) { dmap.put((double)start, cs); } if (!dmap.containsKey(end - 0.5)) { dmap.put(end - 0.5, ce); } events.add(new int[]{start, end}); return true; }

TODO
https://leetcode.com/problems/my-calendar-ii/discuss/109528/nlogd-Java-solution-using-segment-tree-with-lazy-propagation-applicable-to-the-general-case-of-K-booking
http://yueguo1217.com/leetcode-647-palindromic-substrings-median-54-in-python-2/