Massive Algorithms: LeetCode 743

LeetCode 743 - Network Delay Time

https://leetcode.com/problems/network-delay-time/description/

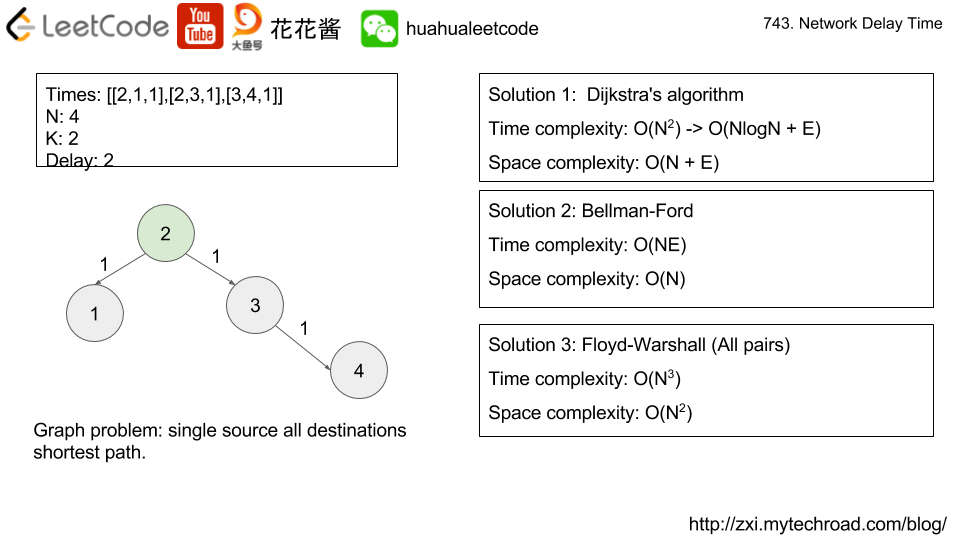
There are N network nodes, labelled 1 to N.

Given times, a list of travel times as directed edges times[i] = (u, v, w), where u is the source node, v is the target node, and w is the time it takes for a signal to travel from source to target.

Now, we send a signal from a certain node K. How long will it take for all nodes to receive the signal? If it is impossible, return -1.

Note:

N will be in the range [1, 100].
K will be in the range [1, N].
The length of times will be in the range [1, 6000].
All edges times[i] = (u, v, w) will have 1 <= u, v <= N and 1 <= w <= 100.

X. Dijkstra - BFS+PQ
http://www.cnblogs.com/grandyang/p/8278115.html
这道题给了我们一些有向边，又给了一个结点K，问至少需要多少时间才能从K到达任何一个结点。这实际上是一个有向图求最短路径的问题，我们求出K点到每一个点到最短路径，然后取其中最大的一个就是需要的时间了。可以想成从结点K开始有水流向周围扩散，当水流到达最远的一个结点时，那么其他所有的结点一定已经流过水了。最短路径的常用解法有迪杰克斯特拉算法Dijkstra Algorithm, 弗洛伊德算法Floyd-Warshall Algorithm, 和贝尔曼福特算法Bellman-Ford Algorithm，其中，Floyd算法是多源最短路径，即求任意点到任意点到最短路径，而Dijkstra算法和Bellman-Ford算法是单源最短路径，即单个点到任意点到最短路径。这里因为起点只有一个K，所以使用单源最短路径就行了。这三种算法还有一点不同，就是Dijkstra算法处理有向权重图时，权重必须为正，而另外两种可以处理负权重有向图，但是不能出现负环，所谓负环，就是权重均为负的环。为啥呢，这里要先引入松弛操作Relaxtion，这是这三个算法的核心思想，当有对边 (u, v) 是结点u到结点v，如果 dist(v) > dist(u) + w(u, v)，那么 dist(v) 就可以被更新，这是所有这些的算法的核心操作。Dijkstra算法是以起点为中心，向外层层扩展，直到扩展到终点为止。根据这特性，用BFS来实现时再好不过了，注意while循环里的第一层for循环，这保证了每一层的结点先被处理完，才会进入进入下一层，这种特性在用BFS遍历迷宫统计步数的时候很重要。对于每一个结点，我们都跟其周围的结点进行Relaxtion操作，从而更新周围结点的距离值。为了防止重复比较，我们需要使用visited数组来记录已访问过的结点，最后我们在所有的最小路径中选最大的返回，注意，如果结果res为INT_MAX，说明有些结点是无法到达的，返回-1。普通的实现方法的时间复杂度为O(V²)，基于优先队列的实现方法的时间复杂度为O(E + VlogV)，其中V和E分别为结点和边的个数，这里多说一句，Dijkstra算法这种类贪心算法的机制，使得其无法处理有负权重的最短距离，还好这道题的权重都是正数

https://github.com/YaokaiYang-assaultmaster/LeetCode/blob/master/LeetcodeAlgorithmQuestions/743.%20Network%20Delay%20Time.md

    public int networkDelayTime(int[][] times, int N, int K) {
        Map<Integer, List<int[]>> adjList = new HashMap<>();
        for (int[] time : times) {
            adjList.computeIfAbsent(time[0], k -> new ArrayList<>()).add(new int[]{time[1], time[2]});
        }
        
        Map<Integer, Integer> dist = new HashMap<>();
        PriorityQueue<int[]> minHeap = new PriorityQueue<>((edge1, edge2) -> {
            return edge1[1] - edge2[1];
        });
        minHeap.offer(new int[]{K, 0});
        
        while (!minHeap.isEmpty()) {
            int[] curr = minHeap.poll();
            if (dist.containsKey(curr[0])) continue;
            dist.put(curr[0], curr[1]);
            if (adjList.containsKey(curr[0])) {
                for (int[] edge : adjList.get(curr[0])) {
                    minHeap.offer(new int[]{edge[0], edge[1] + curr[1]});
                }
            }
        }
        
        if (dist.size() != N) return -1;
        int ret = Integer.MIN_VALUE;
        for (int k : dist.keySet()) {
            ret = Math.max(ret, dist.get(k));
        }
        
        return ret;
    }

We use Dijkstra's algorithm to find the shortest path from our source to all targets. This is a textbook algorithm, refer to this link for more details.

Dijkstra's algorithm is based on repeatedly making the candidate move that has the least distance travelled.

In our implementations below, we showcase both

O(N^2)

(basic) and

O(N \log N)

(heap) approaches.

Time Complexity: $O(N^2 + E)$ m where $E$ is the length of times in the basic implementation, and $O(E \log E)$ in the heap implementation, as potentially every edge gets added to the heap.
Space Complexity: $O(N + E)$ , the size of the graph ( $O(E)$ ), plus the size of the other objects used ( $O(N)$ ).

public int networkDelayTime(int[][] times, int N, int K) {

Map<Integer, List<int[]>> graph = new HashMap();

for (int[] edge : times) {

if (!graph.containsKey(edge[0]))

graph.put(edge[0], new ArrayList<int[]>());

graph.get(edge[0]).add(new int[] { edge[1], edge[2] });

}

PriorityQueue<int[]> heap = new PriorityQueue<int[]>((info1, info2) -> info1[0] - info2[0]);

heap.offer(new int[] { 0, K });

Map<Integer, Integer> dist = new HashMap();

while (!heap.isEmpty()) {

int[] info = heap.poll();

int d = info[0], node = info[1];

if (dist.containsKey(node))

continue;

dist.put(node, d);

if (graph.containsKey(node))

for (int[] edge : graph.get(node)) {

int nei = edge[0], d2 = edge[1];

if (!dist.containsKey(nei))

heap.offer(new int[] { d + d2, nei });

}

if (dist.size() != N)

return -1;

int ans = 0;

for (int cand : dist.values())

ans = Math.max(ans, cand);

return ans;

}

public int networkDelayTime(int[][] times, int n, int k) {

Map<Integer, Map<Integer, Integer>> graph = buildGraph(times);

Map<Integer, Integer> distances = bfs(graph, k);

if (distances.size() < n) {// \\

return -1;

}

return distances.values().stream().max(Comparator.naturalOrder()).get();

}

private Map<Integer, Integer> bfs(Map<Integer, Map<Integer, Integer>> graph, int k) {

PriorityQueue<NodeDistance> pq = new PriorityQueue<>();

Map<Integer, Integer> distances = new HashMap<>();

distances.put(k, 0);// \\

addNeighbourss(pq, distances, k, graph.get(k), 0);

while (!pq.isEmpty()) {

NodeDistance node = pq.poll();

if (distances.containsKey(node.node))

continue;

distances.put(node.node, node.distance);

addNeighbourss(pq, distances, node.node, graph.get(node.node), node.distance);

}

return distances;

}

private void addNeighbourss(PriorityQueue<NodeDistance> pq, Map<Integer, Integer> distances, int k,

Map<Integer, Integer> nbs, int preDistance) {

if (nbs != null) {

for (Entry<Integer, Integer> entry : nbs.entrySet()) {

if (!distances.containsKey(entry.getKey())) {

pq.add(new NodeDistance(entry.getKey(), preDistance + entry.getValue()));

}

private static class NodeDistance implements Comparable<NodeDistance> {

private int node;

private int distance;

public NodeDistance(int node, int distance) {

super();

this.node = node;

this.distance = distance;

}

@Override

public int compareTo(NodeDistance o) {

return Integer.compare(this.distance, o.distance);

}

private Map<Integer, Map<Integer, Integer>> buildGraph(int[][] times) {

Map<Integer, Map<Integer, Integer>> graph = new HashMap<>();

for (int i = 0; i < times.length; i++) {

graph.computeIfAbsent(times[i][0], k -> new HashMap<>()).put(times[i][1], times[i][2]);

}

return graph;

}

basic implementation:
Map<Integer, Integer> dist;
public int networkDelayTime(int[][] times, int N, int K) {
Map<Integer, List<int[]>> graph = new HashMap();
for (int[] edge: times) {
if (!graph.containsKey(edge[0]))
graph.put(edge[0], new ArrayList<int[]>());
graph.get(edge[0]).add(new int[]{edge[1], edge[2]});
}
dist = new HashMap();
for (int node = 1; node <= N; ++node)
dist.put(node, Integer.MAX_VALUE);

dist.put(K, 0);
boolean[] seen = new boolean[N+1];

while (true) {
int candNode = -1;
int candDist = Integer.MAX_VALUE;
for (int i = 1; i <= N; ++i) {
if (!seen[i] && dist.get(i) < candDist) {
candDist = dist.get(i);
candNode = i;
}
}

if (candNode < 0) break;
seen[candNode] = true;
if (graph.containsKey(candNode))
for (int[] info: graph.get(candNode))
dist.put(info[0],
Math.min(dist.get(info[0]), dist.get(candNode) + info[1]));
}

int ans = 0;
for (int cand: dist.values()) {
if (cand == Integer.MAX_VALUE) return -1;
ans = Math.max(ans, cand);
}
return ans;
}

X. DFS
https://leetcode.com/problems/network-delay-time/solution/

We'll maintain dist[node], the earliest that we arrived at each node. When visiting a node while elapsedtime has elapsed, if this is the currently-fastest signal at this node, let's broadcast signals from this node.

To speed things up, at each visited node we'll consider signals exiting the node that are faster first, by sorting the edges.

Time Complexity: $O(N^N + E \log E)$ where $E$ is the length of times. We can only fully visit each node up to $N-1$ times, one per each other node. Plus, we have to explore every edge and sort them. Sorting each small bucket of outgoing edges is bounded by sorting all of them, because of repeated use of the inequality $x \log x + y \log y \leq (x+y) \log (x+y)$ .
Space Complexity: $O(N + E)$ , the size of the graph ( $O(E)$ ), plus the size of the implicit call stack in our DFS ( $O(N)$ ).

Map<Integer, Integer> dist;
public int networkDelayTime(int[][] times, int N, int K) {
Map<Integer, List<int[]>> graph = new HashMap();
for (int[] edge: times) {
if (!graph.containsKey(edge[0]))
graph.put(edge[0], new ArrayList<int[]>());
graph.get(edge[0]).add(new int[]{edge[2], edge[1]});
}
for (int node: graph.keySet()) {
Collections.sort(graph.get(node), (a, b) -> a[0] - b[0]);
}
dist = new HashMap();
for (int node = 1; node <= N; ++node)
dist.put(node, Integer.MAX_VALUE);

dfs(graph, K, 0);
int ans = 0;
for (int cand: dist.values()) {
if (cand == Integer.MAX_VALUE) return -1;
ans = Math.max(ans, cand);
}
return ans;
}

public void dfs(Map<Integer, List<int[]>> graph, int node, int elapsed) {
if (elapsed >= dist.get(node)) return;
dist.put(node, elapsed);
if (graph.containsKey(node))
for (int[] info: graph.get(node))
dfs(graph, info[1], elapsed + info[0]);
}

X. Bellman Ford

下面来看基于Bellman-Ford算法的解法，时间复杂度是O(VE)，V和E分别是结点和边的个数。这种算法是基于DP来求全局最优解，原理是对图进行V - 1次松弛操作，这里的V是所有结点的个数（为啥是V-1次呢，因为最短路径最多只有V-1条边，所以只需循环V-1次），在重复计算中，使得每个结点的距离被不停的更新，直到获得最小的距离，这种设计方法融合了暴力搜索之美，写法简洁又不失优雅。之前提到了，Bellman-Ford算法可以处理负权重的情况，但是不能有负环存在，一般形式的写法中最后一部分是检测负环的，如果存在负环则报错。不能有负环原因是，每转一圈，权重和都在减小，可以无限转，那么最后的最小距离都是负无穷，无意义了。没有负环的话，V-1次循环后各点的最小距离应该已经收敛了，所以在检测负环时，就再循环一次，如果最小距离还能更新的话，就说明存在负环。这道题由于不存在负权重，所以就不检测了
https://leetcode.com/problems/network-delay-time/discuss/109982/C%2B%2B-Bellman-Ford

The solution actually use some thought of dynamical programming
Subproblem: dp(i) represents minimum distance from K to i (iteratively update dp(i) when we find another shorter distance from K to i)
Base case 1:
- initialize MAX value as initial minimum distance from K to every point
- initialize 0 as min distance to K itself
Recurrence relation: traverse all destinations, if dp[u] (starting point of current edge) has already been visited, and new distance from u to v is smaller than previous saved distance, we should update minimum distance from u to v
After getting minimum distance (travel time) to all points, we should retrieve the max distance from these minimum distance, to ensure that we can travel all points in a specific travel time
If we do not visit all points, we should return -1

Complexity is O(VE), but the problem said N will be no more than 100, so the complexity should be O(E)

public int networkDelayTime(int[][] times, int N, int K) {
    if (times == null || times.length == 0) {
        return -1;
    }

    /* Subproblem: dp(i) represents minimum distance from K to i (iteratively update dp(i) when we find another shorter distance from K to i)*/
    int[] dp = new int[N + 1];

    /* Base case 1: initialize MAX value as initial minimum distance from K to every point*/
    /* Base case 2: initialize 0 as min distance to K itself*/
    for (int i = 0; i < N + 1; i++) {
        dp[i] = Integer.MAX_VALUE;
    }
    dp[K] = 0;

    /* traverse all destinations*/
    for (int i = 0; i < N; i++) {
        for (int[] edge : times) {
            int u = edge[0], v = edge[1], w = edge[2];

            /* if dp[u] (starting point of current edge) has already been visited, and new distance from u to v is smaller than previous saved distance
            we should update minimum distance from u to v*/
            if (dp[u] != Integer.MAX_VALUE && dp[v] > dp[u] + w) {
                dp[v] = dp[u] + w;
            }
        }
    }

    /* after getting minimum distance (travel time) to all points, we should retrieve the max distance from these minimum distance, 
     * to ensure that we can travel all points in a specific travel time
    */
    int result = 0;
    for (int i = 1; i <= N; i++) {
        result = Math.max(result, dp[i]);
    }
    /* if we do not visit all points, we should return -1*/
    return result == Integer.MAX_VALUE ? -1 : result;
}

下面这种解法是Bellman Ford解法的优化版本，由热心网友旅叶提供。之所以能提高运行速度，是因为我们使用了队列queue，这样对于每个结点，我们不用都松弛所有的边，因为大多数的松弛计算都是无用功。优化的方法是，若某个点的dist值不变，我们不去更新它，只有当某个点的dist值被更新了，我们才将其加入queue，并去更新跟其相连的点，同时还需要加入HashSet，以免被反复错误更新，这样的时间复杂度可以优化到 O(E+V)。Java版的代码在评论区三楼，旅叶声称可以beat百分之九十多，但博主改写的这个C++版本的却只能beat百分之二十多，hmm，因缺斯汀。不过还是要比上面的解法二快很多，博主又仔细看了看，发现很像解法一和解法二的混合版本哈

    int networkDelayTime(vector<vector<int>>& times, int N, int K) {
        int res = 0;
        unordered_map<int, vector<pair<int, int>>> edges;
        vector<int> dist(N + 1, INT_MAX);
        queue<int> q{{K}};
        dist[K] = 0;
        for (auto e : times) edges[e[0]].push_back({e[1], e[2]});
        while (!q.empty()) {
            int u = q.front(); q.pop();
            unordered_set<int> visited;
            for (auto e : edges[u]) {
                int v = e.first, w = e.second;
                if (dist[u] != INT_MAX && dist[u] + w < dist[v]) {
                    dist[v] = dist[u] + w;
                    if (visited.count(v)) continue;
                    visited.insert(v);
                    q.push(v);
                }
            }
        }
        for (int i = 1; i <= N; ++i) {
            res = max(res, dist[i]);
        }
        return res == INT_MAX ? -1 : res;
    }

再来说说这个Floyd算法，这也是一种经典的动态规划算法，目的是要找结点i到结点j的最短路径。而结点i到结点j的走法就两种可能，一种是直接从结点i到结点j，另一种是经过若干个结点k到达结点j。所以对于每个中间结点k，我们检查dist(i, k) + dist(k, j) < dist(i, j) 是否成立，成立的话就松弛它，这样遍历完所有的结点k，dist(i, j)中就是结点i到结点j的最短距离了。时间复杂度是O(V³)，处处透露着暴力美学。除了这三种算法外，还有一些很类似的优化算法，比如Bellman-Ford的优化算法-SPFA算法，还有融合了Bellman-Ford和Dijkstra算法的高效的多源最短路径算法-Johnson算法

LeetCode 743 - Network Delay Time

Labels

Popular Posts