https://leetcode.com/articles/largest-triangle-area/
https://leetcode.com/problems/largest-triangle-area/discuss/122711/C%2B%2BJavaPython-Solution-with-Explanation-and-Prove
You have a list of points in the plane. Return the area of the largest triangle that can be formed by any 3 of the points.
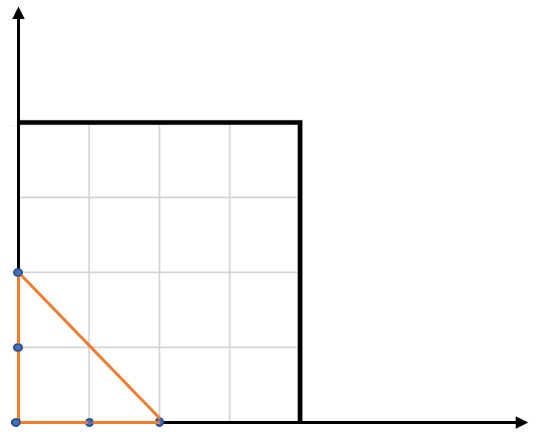
Example: Input: points = [[0,0],[0,1],[1,0],[0,2],[2,0]] Output: 2 Explanation: The five points are show in the figure below. The red triangle is the largest.

Approach #1: Brute Force [Accepted]
For each possible triangle, check it's area and keep the area of the largest.
For each possible triangle, check it's area and keep the area of the largest.
Algorithm
We will have 3 for loops to cycle through each choice of 3 points in the array.
After, we'll need a function to calculate the area given 3 points. Here we have some options:
- We can use the Shoelace formula directly, which tells us the area given the 3 points;
- We can use Heron's formula, which requires the 3 side lengths which we can get by taking the distance of two points;
- We can use the formula
area = 0.5 * a * b * sin(C)and calculate the angleCwith trigonometry.
Our implementation illustrates the use of the shoelace formula.
If we did not know the shoelace formula, we could derive it for triangles with the following approach: starting with points
(px, py), (qx, qy), (rx, ry), the area of this triangle is the same under a translation by (-rx, -ry), so that the points become (px-rx, py-ry), (qx-rx, qy-ry), (0, 0).
From there, we could draw a square around the triangle with sides touching the coordinate axes, and calculate the area of the square minus the area of the right triangles surrounding the inner triangle.
- Time Complexity: , where is the length of
points. We use three for-loops of length , and our work calculating the area of a single triangle is .
public double largestTriangleArea(int[][] points) {
int N = points.length;
double ans = 0;
for (int i = 0; i < N; ++i)
for (int j = i + 1; j < N; ++j)
for (int k = j + 1; k < N; ++k)
ans = Math.max(ans, area(points[i], points[j], points[k]));
return ans;
}
public double area(int[] P, int[] Q, int[] R) {
return 0.5 * Math.abs(P[0] * Q[1] + Q[0] * R[1] + R[0] * P[1] - P[1] * Q[0] - Q[1] * R[0] - R[1] * P[0]);
}
https://leetcode.com/problems/largest-triangle-area/discuss/122711/C%2B%2BJavaPython-Solution-with-Explanation-and-Prove
Burete force loop on all combinations of three points and calculate the area of these three points.
If you google "three pointes triangle area formula", you can find the answer with the first result in second.
If you google "three pointes triangle area formula", you can find the answer with the first result in second.
Time complexity
You may find convex hull first as @weidairpi replies. It help improve to O(M^3 + NlogN) in the best case where M is the number of points on the hull.
But it make this easy problem complex and it stays same complexity in the worst case.
O(N^3) solution, but N <= 50, so it's fast enough.You may find convex hull first as @weidairpi replies. It help improve to O(M^3 + NlogN) in the best case where M is the number of points on the hull.
But it make this easy problem complex and it stays same complexity in the worst case.
Prove 1
Well, someone complains the situation without any formula.
In fact the formula is not that difficult to find out.
Well, someone complains the situation without any formula.
In fact the formula is not that difficult to find out.
For this case:
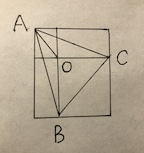

We can calculate the area as follow:
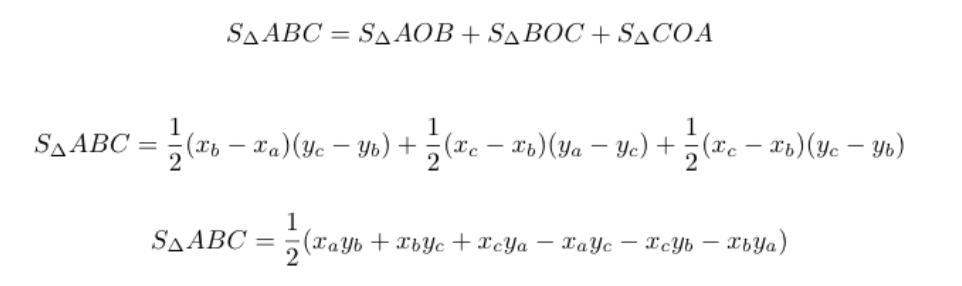
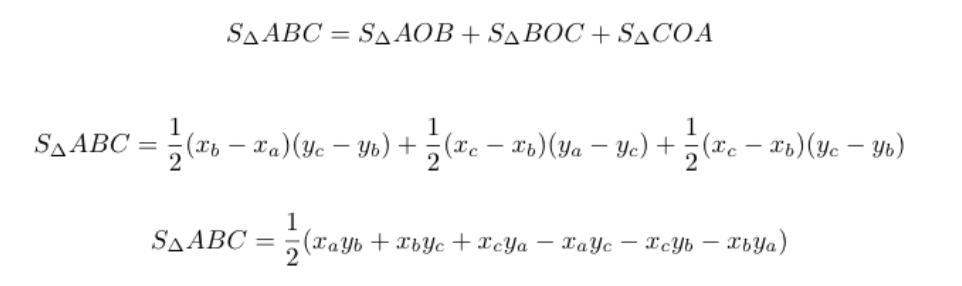
In the result A,B,C are symmetrical, so it won't matter what order we name it.
In this case, we calculate the total area by addition three triangle.
In the other cases, you may need to use substraction and it's quite the same process.
In this case, we calculate the total area by addition three triangle.
In the other cases, you may need to use substraction and it's quite the same process.
Prove 2
If you are familar with vector product. The result is quite obvious.
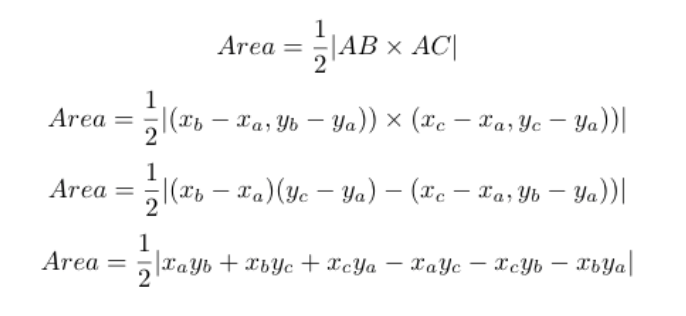
https://leetcode.com/problems/largest-triangle-area/discuss/179046/C
If you are familar with vector product. The result is quite obvious.
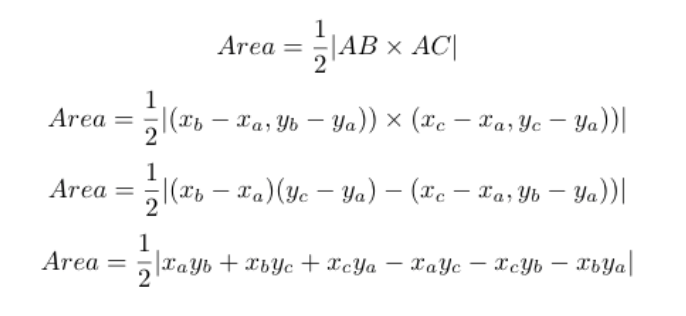
https://leetcode.com/problems/largest-triangle-area/discuss/179046/C
这里使用的是Graham扫描法,将
int[]表示的点封装成了Vector3,并实现了叉乘等常用方法方便计算。虽然暴力法可以通过,但是通过优化可以学习更多新的知识和技术,提高自己解决问题的能力,不要为了做题而做题!public class Solution {
public double LargestTriangleArea(int[][] points) {
double maxArea = -1;
points = Graham(points);
// foreach(var p in resultArray) {
// Console.WriteLine("x:{0}, y:{1}", p[0], p[1]);
// }
for (int i = 0; i < points.Length; i++) {
for (int j = 0; j < points.Length; j++) {
for (int k = 0; k < points.Length; k++) {
if (i != j && j != k && i != k) {
double area = GetTriArea(points[i],points[j],points[k]);
if (area > maxArea) {
maxArea = area;
}
}
}
}
}
return maxArea;
}
private int[][] Graham(int[][] pointsArray) {
List<Vector3> points = new List<Vector3>(pointsArray.Length);
foreach(var p in pointsArray) {
points.Add(new Vector3(p));
}
List<Vector3> result = new List<Vector3>();
for(int i = 0; i < points.Count; i++)
{
//grab the bottom-right point and move it to the head of the list
if (points[i].z < points[0].z || points[i].z == points[0].z && points[i].x > points[0].x)
{
Vector3 temp = points[i];
points[i] = points[0];
points[0] = temp;
}
}
//根据极角由小到大排序
PolarAngleComparer comparer = new PolarAngleComparer(points[0]);
points.Sort(1, points.Count - 1, comparer);
Stack<Vector3> s = new Stack<Vector3>();
s.Push(points[0]);
s.Push(points[1]);
int index = 2;
while (index < points.Count)
{
Vector3 lastPoint = s.Pop();
Vector3 lastSecondPoint = s.Peek();
s.Push(lastPoint);
Vector3 curPoint = points[index];
Vector3 p1 = lastPoint - lastSecondPoint;
Vector3 p2 = curPoint - lastPoint;
Vector3 cross = Vector3.Cross(p1, p2);
//这里使用的是左手坐标系
if (cross.y < 0) //是凸包上的点
{
s.Push(curPoint);
index++;
}
else if (cross.y == 0) //同一直线上,选取离倒数第二个点较远的点
{
double dis1 = Vector3.Distance(lastPoint, lastSecondPoint);
double dis2 = Vector3.Distance(curPoint, lastSecondPoint);
if (dis2 > dis1)
{
s.Pop();
s.Push(curPoint);
}
index++;
}
else //不是凸包上的点
{
s.Pop();
}
}
while (s.Count > 0)
{
result.Add(s.Pop());
}
int[][] resultArray = new int[result.Count][];
for (int i = 0; i < result.Count; i++) {
resultArray[i] = new int[2]{(int)result[i].x, (int)result[i].z};
}
return resultArray;
}
private double GetTriArea(int[] a, int[] b, int[] c)
{
//叉乘计算三角形面积
return (0.5 * Math.Abs(a[0] * b[1] + b[0] * c[1] + c[0] * a[1]- b[0] * a[1] - c[0] * b[1] - a[0] * c[1]));
}
}
//坐标点结构体封装
public struct Vector3 {
public double x;
public double y;
public double z;
public Vector3(double x, double y, double z)
{
this.x = x;
this.y = y;
this.z = z;
}
public Vector3(int[] pointArray)
{
x = pointArray[0];
y = 0;
z = pointArray[1];
}
public static Vector3 zero => new Vector3(0,0,0);
public static Vector3 right => new Vector3(1, 0, 0);
public Vector3 normalized => Normalize(this);
public static Vector3 Cross(Vector3 lhs, Vector3 rhs)
{
return new Vector3(lhs.y * rhs.z - lhs.z * rhs.y, lhs.z * rhs.x - lhs.x * rhs.z, lhs.x * rhs.y - lhs.y * rhs.x);
}
public static double Distance(Vector3 a, Vector3 b)
{
Vector3 vector = new Vector3(a.x - b.x, a.y - b.y, a.z - b.z);
return Math.Sqrt(vector.x * vector.x + vector.y * vector.y + vector.z * vector.z);
}
public static double Dot(Vector3 lhs, Vector3 rhs)
{
return lhs.x * rhs.x + lhs.y * rhs.y + lhs.z * rhs.z;
}
public static Vector3 Normalize(Vector3 value)
{
double num = Magnitude(value);
if (num > 1E-05f)
{
return value / num;
}
return zero;
}
public static double Magnitude(Vector3 a)
{
return Math.Sqrt(a.x * a.x + a.y * a.y + a.z * a.z);
}
public static Vector3 operator +(Vector3 a, Vector3 b)
{
return new Vector3(a.x + b.x, a.y + b.y, a.z + b.z);
}
public static Vector3 operator -(Vector3 a, Vector3 b)
{
return new Vector3(a.x - b.x, a.y - b.y, a.z - b.z);
}
public static Vector3 operator -(Vector3 a)
{
return new Vector3(0f - a.x, 0f - a.y, 0f - a.z);
}
public static Vector3 operator *(Vector3 a, double d)
{
return new Vector3(a.x * d, a.y * d, a.z * d);
}
public static Vector3 operator *(float d, Vector3 a)
{
return new Vector3(a.x * d, a.y * d, a.z * d);
}
public static Vector3 operator /(Vector3 a, double d)
{
return new Vector3(a.x / d, a.y / d, a.z / d);
}
}
//极角排序器
public class PolarAngleComparer : IComparer<Vector3>
{
public Vector3 basePoint = Vector3.zero;
public PolarAngleComparer(Vector3 basePoint)
{
this.basePoint = basePoint;
}
public int Compare(Vector3 x, Vector3 y)
{
Vector3 v1 = x - basePoint;
Vector3 v2 = y - basePoint;
double cos1 = Vector3.Dot(v1.normalized, Vector3.right);
double cos2 = Vector3.Dot(v2.normalized, Vector3.right);
return cos1 < cos2 ? 1 : cos1 > cos2 ? -1 : 0;
}
}