LeetCode 802 - Find Eventual Safe States

https://leetcode.com/problems/find-eventual-safe-states/description/

In a directed graph, we start at some node and every turn, walk along a directed edge of the graph.  If we reach a node that is terminal (that is, it has no outgoing directed edges), we stop.

Now, say our starting node is eventually safe if and only if we must eventually walk to a terminal node.  More specifically, there exists a natural number K so that for any choice of where to walk, we must have stopped at a terminal node in less than K steps.

Which nodes are eventually safe?  Return them as an array in sorted order.

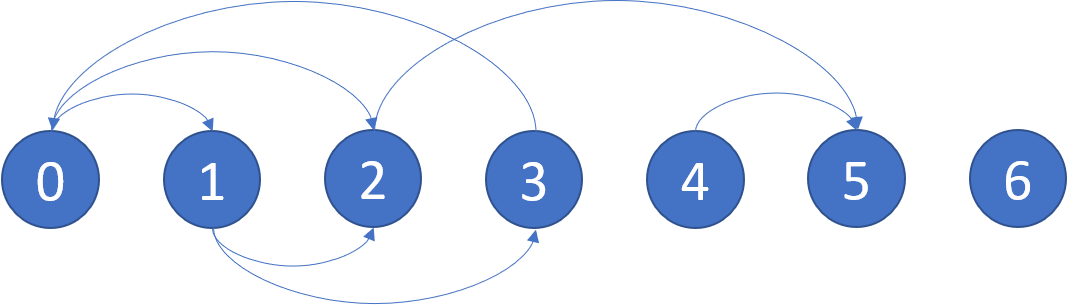
The directed graph has N nodes with labels 0, 1, ..., N-1, where N is the length of graph.  The graph is given in the following form: graph[i] is a list of labels j such that (i, j) is a directed edge of the graph.

Example:
Input: graph = [[1,2],[2,3],[5],[0],[5],[],[]]
Output: [2,4,5,6]
Here is a diagram of the above graph.

Note:

• graph will have length at most 10000.
• The number of edges in the graph will not exceed 32000.
• Each graph[i] will be a sorted list of different integers, chosen within the range [0, graph.length - 1].

https://leetcode.com/problems/find-eventual-safe-states/discuss/119843/Just-DFS-Python-Finding-cycles

The idea is to just use plain DFS with a state = {Initial=0, InProgress=1, Completed=2 }.
When traversing through the graph, if we detect a cycle by encountering a node which is InProgress
if visited[node] == 1
OR
by visiting a node that is already part of a cycle
node in cycle
these two imply that the path we have constructed/traversed so far, all the nodes in the path, are connected to a cycle, so we add them to the cycle set()

cycle |= set(path)

https://leetcode.com/problems/find-eventual-safe-states/discuss/120633/Java-Solution-(DFS-andand-Topological-Sort)

when color[i] = 1 means node i is visiting.
when color[i] = 0 means node i is not visited.
when color[i] = 2 means node i has been already visited.
when color[i] = 1 and it is visited again, it is not safe, otherwise it is safe.

    public List<Integer> eventualSafeNodes(int[][] graph) {
       int N = graph.length;
       int[] color = new int[N];
       List<Integer> res = new ArrayList<>();
       for (int i = 0; i < N; i++) {
           if (dfs(i, color, graph))
               res.add(i);
       }
       return res;
   }
   private boolean dfs(int i, int[] color, int[][] graph) {
       if (color[i] > 0) {
           return color[i] == 2;
       }
       
       color[i] = 1;
       for (int neighbor : graph[i]) {
           if (color[neighbor] == 2) continue;
           
           if (color[neighbor] == 1 || !dfs(neighbor, color, graph)) 
               return false;
       }
       color[i] = 2;
       return true;
   }

https://leetcode.com/problems/find-eventual-safe-states/solution/

The crux of the problem is whether you can reach a cycle from the node you start in. If you can, then there is a way to avoid stopping indefinitely; and if you can't, then after some finite number of steps you'll stop.

Thinking about this property more, a node is eventually safe if all it's outgoing edges are to nodes that are eventually safe.

This gives us the following idea: we start with nodes that have no outgoing edges - those are eventually safe. Now, we can update any nodes which only point to eventually safe nodes - those are also eventually safe. Then, we can update again, and so on.

However, we'll need a good algorithm to make sure our updates are efficient.

Algorithm

We'll keep track of graph, a way to know for some node i, what the outgoing edges (i, j) are. We'll also keep track of rgraph, a way to know for some node j, what the incoming edges (i, j) are.

Now for every node j which was declared eventually safe, we'll process them in a queue. We'll look at all parents i = rgraph[j] and remove the edge (i, j) from the graph (from graph). If this causes the graphto have no outgoing edges graph[i], then we'll declare it eventually safe and add it to our queue.

Also, we'll keep track of everything we ever added to the queue, so we can read off the answer in sorted order later.

    public List<Integer> eventualSafeNodes(int[][] G) {

        int N = G.length;

        boolean[] safe = new boolean[N];

        List<Set<Integer>> graph = new ArrayList();

        List<Set<Integer>> rgraph = new ArrayList();

        for (int i = 0; i < N; ++i) {

            graph.add(new HashSet());

            rgraph.add(new HashSet());

        }

        Queue<Integer> queue = new LinkedList();

        for (int i = 0; i < N; ++i) {

            if (G[i].length == 0)

                queue.offer(i);

            for (int j: G[i]) {

                graph.get(i).add(j);

                rgraph.get(j).add(i);

            }

        }

        while (!queue.isEmpty()) {

            int j = queue.poll();

            safe[j] = true;

            for (int i: rgraph.get(j)) {

                graph.get(i).remove(j);

                if (graph.get(i).isEmpty())

                    queue.offer(i);

            }

        }

        List<Integer> ans = new ArrayList();

        for (int i = 0; i < N; ++i) if (safe[i])

            ans.add(i);

        return ans;

    }

2. DFS
https://leetcode.com/problems/find-eventual-safe-states/discuss/119871/Straightforward-Java-solution-easy-to-understand!

value of color represents three states:
0:have not been visited
1:safe
2:unsafe
For DFS,we need to do some optimization.When we travel a path,we mark the node with 2 which represents having been visited,and when we encounter a node which results in a cycle,we return false,all node in the path stays 2 and it represents unsafe.And in the following traveling,whenever we encounter a node which points to a node marked with 2,we know it will results in a cycle,so we can stop traveling.On the contrary,when a node is safe,we can mark it with 1 and whenever we encounter a safe node,we know it will not results in a cycle.

It's better to use enum instead of int constants. For more info see Item 34 Effective Java 3rd Edition.

Time complexity: O(V + E)
Space complexity: O(V + E)

enum State {
    SAFE,
    UNSAFE
}

public List<Integer> eventualSafeNodes(int[][] graph) {
    List<Integer> safeNodes = new ArrayList<>(graph.length);
    State[] states = new State[graph.length];
    for (int node = 0; node < graph.length; node++) {
        if (isSafe(graph, node, states)) {
            safeNodes.add(node);
        }
    }
    return safeNodes;
}

private boolean isSafe(int[][] graph, int node, State[] states) {
    if (states[node] != null) {
        return states[node] == State.SAFE;
    }

    states[node] = State.UNSAFE;

    for (int next : graph[node]) {
        if (!isSafe(graph, next, states)) return false;
    }

    states[node] = State.SAFE;
    return true;
}

As in Approach #1, the crux of the problem is whether you reach a cycle or not.

Let us perform a "brute force": a cycle-finding DFS algorithm on each node individually. This is a classic "white-gray-black" DFS algorithm that would be part of any textbook on DFS. We mark a node gray on entry, and black on exit. If we see a gray node during our DFS, it must be part of a cycle. In a naive view, we'll clear the colors between each search.

Algorithm

We can improve this approach, by noticing that we don't need to clear the colors between each search.

When we visit a node, the only possibilities are that we've marked the entire subtree black (which must be eventually safe), or it has a cycle and we have only marked the members of that cycle gray. So indeed, the invariant that gray nodes are always part of a cycle, and black nodes are always eventually safe is maintained.

In order to exit our search quickly when we find a cycle (and not paint other nodes erroneously), we'll say the result of visiting a node is true if it is eventually safe, otherwise false. This allows information that we've reached a cycle to propagate up the call stack so that we can terminate our search early.

    public List<Integer> eventualSafeNodes(int[][] graph) {

        int N = graph.length;

        int[] color = new int[N];

        List<Integer> ans = new ArrayList();

        for (int i = 0; i < N; ++i)

            if (dfs(i, color, graph))

                ans.add(i);

        return ans;

    }

    // colors: WHITE 0, GRAY 1, BLACK 2;

    public boolean dfs(int node, int[] color, int[][] graph) {

        if (color[node] > 0)

            return color[node] == 2;

        color[node] = 1;

        for (int nei: graph[node]) {

            if (color[node] == 2)

                continue;

            if (color[nei] == 1 || !dfs(nei, color, graph))

                return false;

        }

        color[node] = 2;

        return true;

    }

X. Reverse Graph
https://leetcode.com/problems/find-eventual-safe-states/discuss/119827/20-line-Python-concise-sol-by-removing-0-out-degree-nodes

This is equal to find nodes which doesn't lead to a circle in any path.
We can solve it by walking along the path reversely.

1. Find nodes with out degree 0, they are terminal nodes, we remove them from graph and they are added to result
2. For nodes who are connected terminal nodes, since terminal nodes are removed, we decrease in-nodes' out degree by 1 and if its out degree equals to 0, it become new terminal nodes
3. Repeat 2 until no terminal nodes can be found.

X. Topological-Sort
https://www.omgleoo.top/leetcode-802-find-eventual-safe-states/

解法一：剔除到终点的边

首先，如果一个点本身就是终点（即没有出去的边），那么该节点就是最终安全的。在示例的图中，节点5和节点6都是终点，因此它们是最终安全的。

另外，如果一个节点所有出去的边都是走向终点的，那么该节点也是最终安全的，因为从该节点出发不会进入一个环。因此，我们找出所有出度为0的节点（开始只有终点是出去为0的节点）。接下来，把进入最终安全的节点的边剔除。剔除边之后如果发现有新的节点的出度变成0，那么该节点也是最终安全的。接下来再剔除进入它们的边。

前面我们已经知道节点5是最终安全的。有两条边进入节点5，分别来至节点2和节点4。在剔除这两条边之后，节点2和节点4的出度都是0，因此它们都是最终安全的。

如果所有进入最终安全的边都剔除后哪个节点仍然还有边出去，那么这些边将进入环。这样的节点不是最终安全的。

在示例图中，在剔除两条进入节点2的边（分别来自节点0和节点1）之后，再也没有其他能够进入最终安全的节点的边了。我们发现剩下3条边，第一条从节点0出发进入节点1，第二条从节点1出发进入节点3，第三条从节点3出发进入节点0。它们形成了一个环，因此它们都不是最终安全的节点。

https://leetcode.com/problems/find-eventual-safe-states/discuss/120633/Java-Solution-(DFS-andand-Topological-Sort)

Method 1: Topological Sort
Using degree array to record the out-degree, neighbors map to record In-neighbors(for example 0->1, 2->1, map(1) = [0, 2]).
Add the node whose out-degree is 0 into queue and result Set, then process each node in the queue, if the out-degree of one node becomes 0, add it to queue until queue is empty.

    public List<Integer> eventualSafeNodes(int[][] graph) {
        int N = graph.length;
        int[] degree = new int[N];
        Map<Integer, Set<Integer>> neighbors = new HashMap<>();
        for (int i = 0; i < graph.length; i++) {
            for (int neighbor : graph[i]) {
                if (!neighbors.containsKey(neighbor)) neighbors.put(neighbor, new HashSet<Integer>());
                neighbors.get(neighbor).add(i);
                degree[i]++;
            }
        }
        
        Set<Integer> res = new HashSet<>();
        Queue<Integer> queue = new LinkedList<>();
        
        for (int i = 0; i < N; i++) {
            if (degree[i] == 0) {
                res.add(i);
                queue.add(i);
            }    
        }
        
        while (!queue.isEmpty()) {
            int v = queue.poll();
            res.add(v);
            if (neighbors.containsKey(v)) {
                for (int neighbor : neighbors.get(v)) {
                    degree[neighbor]--;
                    if (degree[neighbor] == 0) {
                        queue.offer(neighbor);
                    }
                }
            }
            
        }
        List<Integer> list = new ArrayList<Integer>(res);
        Collections.sort(list);
        return list;
    }

https://leetcode.com/problems/find-eventual-safe-states/discuss/119860/Java-O(N)-DFS-Solution-very-similar-to-Course-Schedule

public List<Integer> eventualSafeNodes(int[][] graph) {

List<Integer> result = new ArrayList<>();

if (graph == null)

return result;

Set<Integer> safeNodes = new HashSet<>(), notSafeNodes = new HashSet<>();

for (int i = 0; i < graph.length; i++) {

if (dfs(i, graph, safeNodes, notSafeNodes, new HashSet<>())) {

safeNodes.add(i);

} else {

notSafeNodes.add(i);

}

}

return new ArrayList<>(new TreeSet<>(safeNodes));

}

// is safe(no cycle) or not

private boolean dfs(Integer node, int[][] graph, Set<Integer> safeNodes, Set<Integer> notSafeNodes,

Set<Integer> traverses) {

if (safeNodes.contains(node)) {

return true;

}

if (notSafeNodes.contains(node)) {

return false;

}

if (traverses.contains(node)) {

notSafeNodes.add(node);

return false;

}

traverses.add(node);

boolean safe = true;

// nb short for neighbor

for (Integer nb : graph[node]) {

if (!dfs(nb, graph, safeNodes, notSafeNodes, traverses)) {

safe = false;

}

}

traverses.remove(node);

if (safe) {

safeNodes.add(node);

} else {

notSafeNodes.addAll(traverses);

notSafeNodes.add(node);

}

return safe;

}

X. https://leetcode.com/articles/find-eventual-safe-states/
Approach #1: Reverse Edges [Accepted]
Intuition

The crux of the problem is whether you can reach a cycle from the node you start in. If you can, then there is a way to avoid stopping indefinitely; and if you can't, then after some finite number of steps you'll stop.

Thinking about this property more, a node is eventually safe if all it's outgoing edges are to nodes that are eventually safe.

This gives us the following idea: we start with nodes that have no outgoing edges - those are eventually safe. Now, we can update any nodes which only point to eventually safe nodes - those are also eventually safe. Then, we can update again, and so on.

However, we'll need a good algorithm to make sure our updates are efficient.

Algorithm

We'll keep track of graph, a way to know for some node i, what the outgoing edges (i, j) are. We'll also keep track of rgraph, a way to know for some node j, what the incoming edges (i, j) are.

Now for every node j which was declared eventually safe, we'll process them in a queue. We'll look at all parents i = rgraph[j] and remove the edge (i, j) from the graph (from graph). If this causes the graph to have no outgoing edges graph[i], then we'll declare it eventually safe and add it to our queue.

Also, we'll keep track of everything we ever added to the queue, so we can read off the answer in sorted order later.

Time Complexity: $O(N + E)$, where $N$ is the number of nodes in the given graph, and $E$ is the total number of edges

  public List<Integer> eventualSafeNodes(int[][] G) {

    int N = G.length;

    boolean[] safe = new boolean[N];

    List<Set<Integer>> graph = new ArrayList<>();

    List<Set<Integer>> rgraph = new ArrayList<>();

    for (int i = 0; i < N; ++i) {

      graph.add(new HashSet<>());

      rgraph.add(new HashSet<>());

    }

    Queue<Integer> queue = new LinkedList<>();

    for (int i = 0; i < N; ++i) {

      if (G[i].length == 0)

        queue.offer(i);

      for (int j : G[i]) {

        graph.get(i).add(j);

        rgraph.get(j).add(i);

      }

    }

    while (!queue.isEmpty()) {

      int j = queue.poll();

      safe[j] = true;

      for (int i : rgraph.get(j)) {

        graph.get(i).remove(j);

        if (graph.get(i).isEmpty())

          queue.offer(i);

      }

    }

    List<Integer> ans = new ArrayList<>();

    for (int i = 0; i < N; ++i)

      if (safe[i])

        ans.add(i);

    return ans;

  }