LeetCode 779 - K-th Symbol in Grammar

http://bookshadow.com/weblog/2018/02/04/leetcode-k-th-symbol-in-grammar/

On the first row, we write a 0. Now in every subsequent row, we look at the previous row and replace each occurrence of 0 with 01, and each occurrence of 1 with 10.

Given row N and index K, return the K-th indexed symbol in row N. (The values of K are 1-indexed.) (1 indexed).

Examples:
Input: N = 1, K = 1
Output: 0

Input: N = 2, K = 1
Output: 0

Input: N = 2, K = 2
Output: 1

Input: N = 4, K = 5
Output: 1

Explanation:
row 1: 0
row 2: 01
row 3: 0110
row 4: 01101001

X. https://leetcode.com/problems/k-th-symbol-in-grammar/discuss/113710/Python-simple-solution-to-understand-with-explanations
观察一下规律就知道，下一行是左边保留上一行，右边是上一行取反
用递归，已知N == 1的时候返回0，为了知道第N行第K个数字的值，只要知道它在第N-1行的第(K+1)/2个数字对应的值即可，因为0对应01，1对应10，那么如果K是奇数只需和原数字相同即可，如果K是偶数只需对原对应数字取反即可

We don't need to actually generate the strings "0110..." (would be TLE error anyway)

We see that, for any level N, the first half of the string is the same as the string in N-1, the next half is just complement of it. The total number of items in level N is 2^N. The half mark of the string is marked by [2^(N-1)]-th item. So, for any level N:

• if K is in the first half, it is same as the Kth element in level N-1
• if K is in the second half, it is the complement of the number in [K-2^(N-1)]-th position in level N-1

So, we run the recursion until the base condition (N=1)

https://leetcode.com/problems/k-th-symbol-in-grammar/discuss/113697/My-3-lines-C++-recursive-solution

The whole structure can be viewed a binary tree, when a node is 0, their two children nodes are 0 and 1, similarly, when a node is 1, two children nodes are 1 and 0. We can know whether the position of K is a left node or a right node by dividing 2. If K is even, current node is right child, and its parent is the (K/2)th node in previous row; else if K is odd, current node is left child and its parent is the ((K+1)/2)th node in previous row.
The value of current node depends on its parent node, without knowing its parent node value, we still cannot determine current node value. That's why we need recursion, we keep going previous row to find the parent node until reach the first row. Then all the parent node value will be determined after the recursion function returns.

public int kthGrammar(int N, int K) {
    if (N == 1) return 0; //first line only has one number 0
    if (K % 2 == 0) return kthGrammar(N - 1, K / 2) == 0 ? 1 : 0; //If K is even, find the appended number at correct position of previous row
    return kthGrammar(N - 1, (K + 1) / 2); //If K is odd, just find the correct position from previous row
}

X.

Note that N is redundant in this problem.

int kthGrammar(int, int K) {
    return K == 1 ? 0 : (~K & 1) ^ kthGrammar(0, (K + 1) / 2);
}

https://leetcode.com/problems/k-th-symbol-in-grammar/discuss/113721/C++-with-explanation-three-solutions-O(n)-O(logn)-and-O(loglogn)

The structure is like a full tree.
0 ==> 01; 1 ==> 10; so if only if K%2 == 0, result(K) == result(K/2);
The key is whether the set bits of (K-1) is odd or even
O(logn) 3ms

    int kthGrammar(int N, int K) {
        K--;
        int cnt = 0;
        while (K) {
            cnt += K&1;
            K >>= 1;
        }
        return cnt%2;
    }

If we only care about the set bits are odd or even, there is an O(loglogn) solution.
Although O(loglogn) may be meaningless here, because logn is at most 32. Let's assume K is m bits long.

    int kthGrammar(int N, int K) {
       K--;
       int m = 32;
       while (m > 1) {
          m = (m + 1) >> 1;
          K = K ^ (K >> m);
          K &= (1 << m) - 1;
       }
       return K & 1;
    }




X.
https://blog.csdn.net/huanghanqian/article/details/79254001

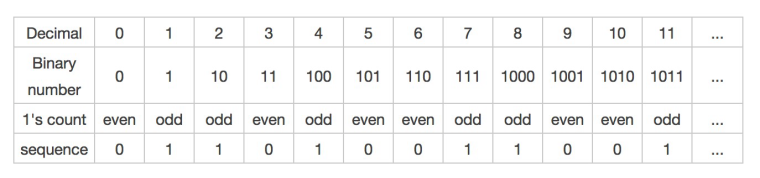
sequence中的序列正好是题目中的序列。

https://leetcode.com/problems/k-th-symbol-in-grammar/discuss/113705/JAVA-one-line

public int kthGrammar(int N, int K) {
    return Integer.bitCount(K-1) & 1;
}

Updates: (all index discussed below are 0-based)
Observation 1: N does not matter as long as "K will be an integer in the range [1, 2^(N-1)]". We can ignore N.

Observation 2: let f(k) be the value of kth position (0-based), then:
f(2 * k) = 0 {if f(k) = 0} or, 1 {if f(k) = 1} => f(2 * k) = f(k) xor 0
f(2 * k + 1) = 0 {if f(k) = 1} or 1 {if f(k) = 0} => f(2 * k + 1) = f(k) xor 1

Obervation 3: if binary string of k is used, let k = 1001010, then we have:
f(1001010) = f(100101) ^ 0 = f(10010) ^ 1 ^ 0 = f(1001) ^ 0 ^ 1 ^ 0 = ... = f(0) ^ 1 ^ 0 ^ 0 ^1 ^ 0 ^ 1 ^ 0 = 1 ^ 0 ^ 0 ^1 ^ 0 ^ 1 ^ 0
So, the result is the xor operation on all bits of k. Since 0 does not change xor result, we can ignore all 0s.
f(1001010) = 1 ^ 1 ^ 1 = (1^1) ^ 1 = 0 ^ 1 = 1
f(11110011) = 1 ^ 1^ 1 ^ 1 ^ 1 ^1 = (1 ^ 1) ^ (1 ^ 1) ^ (1 ^1) = 0
Now, it's easy to tell f(k) = 0 if k has even number of 1s in binary representation, and f(k) = 1 when k has odd number of 1s

     The L_th number in row N-1 will generate 2 numbers in row N at position 2L and 2L+1
     Note the pattern given in the problem 0 -> 01, 1->10.
     This means the first digit will always stay the same, and the second digit will flip between 0 and 1

     Now looking backward, our K could be 2L or 2L+1
     If K is 2L, we know it'll take the same value as L in row N-1.
     If K is 2L+1, it'll take the flipped value
     keep doing this x times until we hit the initial value of 0 in row 1.
     During this x times of recursion, say there are y times where K is odd. Those are the times when the value flipped between 0 and 1
     so the end result is the initial value 0, flipped y times
    
     Now going from K (2L or 2L+1) to L, is really just right shifting K by 1 bit
     Before you shift, check if the least significant bit of K is 1, if so, record one occurrence of an odd number
     essentially this is the same as counting the number of 1's in K's binary representation

https://leetcode.com/problems/k-th-symbol-in-grammar/discuss/113736/PythonJavaC++-Easy-1-line-Solution-with-detailed-explanation

First, you can easily find that prefix of every row is exactly the same.
It not difficult to understand.
Beacause every 2 * L fisrt letters are generated by the same L fist letters.

Then, we know that every row is the start part of the same long sequence.
Moreover K is guaranteed to be an integer in the range[1, 2 ^ (N - 1)].
So result depends only on value K

Suppose 2 ^ L < K <= 2 ^ (L + 1).
2 ^ (L - 1) is the biggest 2's power smaller than K.
Kth number is generated from K - 2 ^ (L - 1)
Kth number is also different from K - 2 ^ (L - 1)
So we toggle K to K - 2 ^ L by subtracting 2 ^ L

We repeat the process until we toggle K to 1, which mean we need to substract K - 1 in total.
What we should do is transfer K - 1 in binary so that we can easily find how many times we need to toggle.

For example K = 8
we need to substract K - 1 = 7 = 111 in binary.
So we need to substract 100, 10 and 1, which are 4, 2, 1 in decimal.
We toggle K from 8 to 4, 2 and finally 1.

For example K = 9
we need to substract K - 1 = 8 = 1000 in binary.
So we need to substract 1000, which is 8 in decimal.
We toggle K from 9 to 1 directly.

Conclusion
we turn this problem to just count 1bits.
We can observe that the answer depend on whether the number of 1 bits in binary K-1 is odd or even.
Now you may have many ways to solve this problem.
In Python, I transfer K to binary.
In Java, bitCount is ready for use.
In C++, I use the trick K & (K - 1) to drops the lowest bit.

Here is another idea:
https://leetcode.com/problems/k-th-symbol-in-grammar/discuss/121544/C++JavaPython-Another-Solution

X.
https://leetcode.com/problems/k-th-symbol-in-grammar/discuss/113721/C++-with-explanation-three-solutions-O(n)-O(logn)-and-O(loglogn)

    int kthGrammar(int N, int K) {
        string s = "0";
        for (int i = 1; i < N; ++i) {
            string t;
            for (char c : s) {
                if (c == '0')
                   t += "01";
                else
                   t += "10";
            }
            swap(s, t);
        }
        return s[K-1]-'0';
    }




// also use too much memory

// TLE, what we don't need to do:

// We don't have to generate the strings for each row

public int kthGrammar(int n, int k) {

if (n < 0 || k < 0) {

return -1;

}

if (k > Math.pow(2, n - 1)) {

return -1;

}

List<Integer> preRow = new ArrayList<>();

for (int i = 0; i < n; i++) {

preRow = nthRowGrammar(preRow);

// System.out.println(preRow);

}

return preRow.get(k - 1);

}

private static Map<List<Integer>, List<Integer>> expandCache = new HashMap<>(); // not good use list as key of map

public List<Integer> nthRowGrammar(List<Integer> preRow) {

if (expandCache.containsKey(preRow)) {

return new ArrayList<>(expandCache.get(preRow));

}

List<Integer> result = new ArrayList<>();

if (preRow.isEmpty()) {

result.add(0);

expandCache.put(preRow, result);

return result;

// return Arrays.asList(0);// Collections.unmodifiableList(Arrays.asList(0));

}

if (preRow.size() == 1) {

int value = preRow.get(0);

if (value == 0) {

result.add(0);

result.add(1);

expandCache.put(preRow, result);

return result;

} else {

result.add(1);

result.add(0);

expandCache.put(preRow, result);

return result;

}

}

result.addAll(nthRowGrammar(preRow.subList(0, preRow.size() / 2)));

result.addAll(nthRowGrammar(preRow.subList(preRow.size() / 2, preRow.size()))); // not preRow.size() -1 [}

expandCache.put(preRow, result);

return result;

}