LeetCode 787 - Cheapest Flights Within K Stops


https://leetcode.com/problems/cheapest-flights-within-k-stops/description/
There are n cities connected by m flights. Each fight starts from city u and arrives at v with a price w.
Now given all the cities and fights, together with starting city src and the destination dst, your task is to find the cheapest price from src to dst with up to k stops. If there is no such route, output -1.
Example 1:
Input: 
n = 3, edges = [[0,1,100],[1,2,100],[0,2,500]]
src = 0, dst = 2, k = 1
Output: 200
Explanation: 
The graph looks like this:


The cheapest price from city 0 to city 2 with at most 1 stop costs 200, as marked red in the picture.
X.  Using PriorityQueue


Time Complexity is O(ElogV) E is the length of flights and V is the number of cities
It happen to be the same idea of Dijkstra's algorithm, but we need to keep the path while explore the grape.
https://leetcode.com/problems/cheapest-flights-within-k-stops/discuss/115541/Easy-and-Concise-Solution-Using-Priority-Queue-JavaPython
We don't need a visited map here, since if a city is visited multiple times(e.g. there is a circle), the distance will increase, which will decrease it's priority in PriorityQueue

 The key difference with the classic Dijkstra algo is, we don't maintain the global optimal distance to each node, i.e. ignore below optimization:
alt ← dist[u] + length(u, v)
if alt < dist[v]:
Because there could be routes which their length is shorter but pass more stops, and those routes don't necessarily constitute the best route in the end. To deal with this, rather than maintain the optimal routes with 0..K stops for each node, the solution simply put all possible routes into the priority queue, so that all of them has a chance to be processed. IMO, this is the most brilliant part.
And the solution simply returns the first qualified route, it's easy to prove this must be the best route.
    public int findCheapestPrice(int n, int[][] flights, int src, int dst, int k) {
        Map<Integer, Map<Integer, Integer>> prices = new HashMap<>();
        for (int[] f : flights) {
            if (!prices.containsKey(f[0])) prices.put(f[0], new HashMap<>());
            prices.get(f[0]).put(f[1], f[2]);
        }
        Queue<int[]> pq = new PriorityQueue<>((a, b) -> (Integer.compare(a[0], b[0])));
        pq.add(new int[] {0, src, k + 1});
        while (!pq.isEmpty()) {
            int[] top = pq.remove();
            int price = top[0];
            int city = top[1];
            int stops = top[2];
            if (city == dst) return price;
            if (stops > 0) {
                Map<Integer, Integer> adj = prices.getOrDefault(city, new HashMap<>());
                for (int a : adj.keySet()) {
                    pq.add(new int[] {price + adj.get(a), a, stops - 1});
                }
            }
        }
        return -1;
    }

X. BFS

https://leetcode.com/problems/cheapest-flights-within-k-stops/discuss/115570/BFS-with-small-tweak-to-guarantee-k-stops
https://leetcode.com/problems/cheapest-flights-within-k-stops/discuss/166443/AC.-Simple-BFS-(5ms)-No-PQ.-Beats-99-of-submissions
The idea is to perform a BFS from src upto only K levels. I initially hit a Memory limit but was able to get around by adding a minPrices check to skip exploring from a node if it does not give better result.
Code below -
    public int findCheapestPrice(int n, int[][] flights, int src, int dst, int K) {
        //convert flights[] to a weighted graph
        //perform BFS starting from src going only max depth of K
        //For Each node track the cost associated to reach that node
        int min = Integer.MAX_VALUE;
        int[][] graph = new int[n][n];
        int[] minPrices = new int[n];
        for (int[] flight : flights) {
            int start = flight[0];
            int end = flight[1];
            graph[start][end] = flight[2];
        }
        Queue<Integer> q = new LinkedList<>();
        Queue<Integer> prices = new LinkedList<>();
        q.add(src);
        prices.add(0);
        while (!q.isEmpty() && K >= 0) {
            K--;
            int size = q.size();
            for (int i = 0; i < size; i++) {
                int start = q.poll();
                int priceTillNow = prices.poll();
                for (int j = 0; j < n; j++) {
                    int price = graph[start][j];
                    if (price > 0) {    //there is a flight
                        int curPrice = priceTillNow + price;
                        int oldPrice = minPrices[j];
                        //If there is a cheaper flight with lesser stops do not add it to q
                        if (oldPrice == 0 || oldPrice > curPrice) {//pruning
                            minPrices[j] = curPrice;
                            q.add(j);
                            prices.add(curPrice);
                            if (j == dst && min > curPrice) {
                                min = curPrice;
                            }
                        }
                    }
                }
            }
        }
        return min == Integer.MAX_VALUE ? -1 : min;
    }
http://zxi.mytechroad.com/blog/dynamic-programming/leetcode-787-cheapest-flights-within-k-stops/
  int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int K) {
    unordered_map<int, vector<pair<int,int>>> g;
    for (const auto& e : flights)
      g[e[0]].emplace_back(e[1], e[2]);
    
    int ans = INT_MAX;
    queue<pair<int,int>> q;
    q.push({src, 0});
    int steps = 0;
    
    while (!q.empty()) {
      int size = q.size();
      while (size--) {
        int curr = q.front().first;
        int cost = q.front().second;
        q.pop();
        if (curr == dst)
          ans = min(ans, cost);
        for (const auto& p : g[curr]) {
          if (cost + p.second > ans) continue; // Important: prunning          
          q.push({p.first, cost + p.second});
        }
      }
      if (steps++ > K) break;
    }
    
    return ans == INT_MAX ? - 1 : ans;
  }

public int findCheapestPrice(int n, int[][] flights, int src, int dst, int K) {

Map<Integer, Map<Integer, Integer>> graph = parseGraph(flights);

Queue<DestPrice> queue = new ArrayDeque<>();

addNeighborToQueue(graph.get(src), new DestPrice(0, 0), queue);

int stop = 0;
boolean canReachDest = false;
int minPrice = Integer.MAX_VALUE;
while (stop <= K) {

int size = queue.size();

for (int i = 0; i < size; i++) {

DestPrice destPrice = queue.poll();

if (destPrice.price >= minPrice) {
continue;
}
if (destPrice.dest == dst) {
canReachDest = true;
minPrice = destPrice.price; // Math.min(minPrice, destPrice.price);
continue;
}

if (stop <= K) {
addNeighborToQueue(graph.get(destPrice.dest), destPrice, queue);
}
}

++stop;

}

return canReachDest ? minPrice : -1;
}

public static class DestPrice {
public final int dest;
public final int price;

public DestPrice(int dest, int price) {
super();
this.dest = dest;
this.price = price;
}
}

private void addNeighborToQueue(Map<Integer, Integer> nbs, DestPrice destPrice, Queue<DestPrice> queue) {
if (nbs == null)
return;

for (Entry<Integer, Integer> entry : nbs.entrySet()) {
queue.add(new DestPrice(entry.getKey(), destPrice.price + entry.getValue()));
}

}

private Map<Integer, Map<Integer, Integer>> parseGraph(int[][] flights) {
Map<Integer, Map<Integer, Integer>> graph = new HashMap<>();
for (int i = 0; i < flights.length; i++) {
graph.computeIfAbsent(flights[i][0], v -> new HashMap<>()).put(flights[i][1], flights[i][2]);
}
return graph; //
}

X. DFS
  int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int K) {
    g_.clear();  
    for (const auto& e : flights)
      g_[e[0]].emplace_back(e[1], e[2]);
    vector<int> visited(n, 0);
    visited[src] = 1;
    int ans = INT_MAX;
    dfs(src, dst, K + 1, 0, visited, ans);
    return ans == INT_MAX ? - 1 : ans;
  }
private:
  unordered_map<int, vector<pair<int,int>>> g_;
  
  void dfs(int src, int dst, int k, int cost, vector<int>& visited, int& ans) {
    if (src == dst) {
      ans = cost;
      return;
    }
    
    if (k == 0) return;    
    
    for (const auto& p : g_[src]) {
      if (visited[p.first]) continue; // do not visit the same city twice.
      if (cost + p.second > ans) continue; // IMPORTANT!!! prunning
      visited[p.first] = 1;
      dfs(p.first, dst, k - 1, cost + p.second, visited, ans);
      visited[p.first] = 0;
    }
  }

X. DP - Bellman-Ford algorithm
https://leetcode.com/problems/cheapest-flights-within-k-stops/discuss/207128/Two-Java-Solutions-one-is-DP-and-the-other-is-Dijkstra
Time Complexity for this solution is O(KN), k is stop and N is the number of cities
public int findCheapestPrice(int n, int[][] flights, int src, int dst, int K) {
        //dp[i][j] denotes the cheapest price within i-1 stops, stop in j city
        long[][] dp = new long[K+2][n];
        for (long[] d : dp) Arrays.fill(d, Integer.MAX_VALUE);
        dp[0][src] = 0;
        for (int i = 1; i < K+2; i++) {
            dp[i][src] = 0;
            for (int[] f : flights) {
                dp[i][f[1]] = Math.min(dp[i][f[1]], dp[i-1][f[0]] + f[2]);
            }
        }
        return dp[K+1][dst] == Integer.MAX_VALUE ? -1 : (int)dp[K+1][dst];
    }
http://www.cnblogs.com/grandyang/p/9109981.html
核心思想还是用的动态规划Dynamic Programming，最核心的部分就是松弛操作Relaxation，也就是DP的状态转移方程。这里我们使用一个二维DP数组，其中dp[i][j]表示最多飞i次航班到达j位置时的最少价格，那么dp[0][src]初始化为0，因为飞0次航班的价格都为0，转机K次，其实就是飞K+1次航班，我们开始遍历，i从1到K+1，每次dp[i][src]都初始化为0，因为在起点的价格也为0，然后即使遍历所有的航班x，更新dp[i][x[1]]，表示最多飞i次航班到达航班x的目的地的最低价格，用最多飞i-1次航班，到达航班x的起点的价格加上航班x的价格之和，二者中取较小值更新即可
    int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int K) {
        vector<vector<int>> dp(K + 2, vector<int>(n, 1e9));
        dp[0][src] = 0;
        for (int i = 1; i <= K + 1; ++i) {
            dp[i][src] = 0;
            for (auto x : flights) {
                dp[i][x[1]] = min(dp[i][x[1]], dp[i - 1][x[0]] + x[2]);
            }
        }
        return (dp[K + 1][dst] >= 1e9) ? -1 : dp[K + 1][dst];
    }

我们可以稍稍优化下上面解法的空间复杂度，使用一个一维的DP数组即可，具体思路没有啥太大的区别，参见代码如下：

    int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int K) {
        vector<int> dp(n, 1e9);
        dp[src] = 0;
        for (int i = 0; i <= K; ++i) {
            vector<int> t = dp;
            for (auto x : flights) {
                t[x[1]] = min(t[x[1]], dp[x[0]] + x[2]);
            }
            dp = t;
        }
        return (dp[dst] >= 1e9) ? -1 : dp[dst];
    }
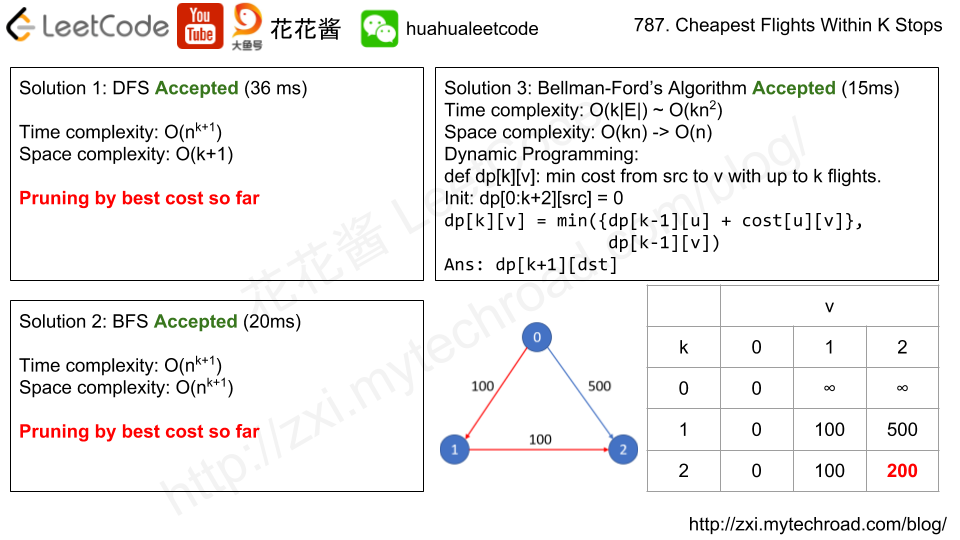
dp[k][i]: min cost from src to i taken up to k flights (k-1 stops)
init: dp[0:k+2][src] = 0
transition: dp[k][i] = min(dp[k-1][j] + price[j][i])
ans: dp[K+1][dst]
Time complexity: O(k * |flights|) / O(k*n^2)
Space complexity: O(k*n) -> O(n)
w/o space compression O(k*n)
  public int findCheapestPrice(int n, int[][] flights, int src, int dst, int K) {
    final int kInfCost = 1<<30;
    int[] cost = new int[n];
    Arrays.fill(cost, kInfCost);
    cost[src] = 0;
    
    for (int i = 0; i <= K; ++i) {
      int[] tmp = cost.clone();
      for(int[] p: flights)
        tmp[p[1]] = Math.min(tmp[p[1]], cost[p[0]] + p[2]);
      cost = tmp;
    }
    
    return cost[dst] >= kInfCost ? -1 : cost[dst];
  }

https://leetcode.com/problems/cheapest-flights-within-k-stops/discuss/163698/easy-java-Bellman-Ford
public int findCheapestPrice(int n, int[][] flights, int src, int dst, int k) {
        int INF = 0x3F3F3F3F;
        int[] cost = new int[n];
        Arrays.fill(cost, INF);
        cost[src] = 0;
        int ans = cost[dst];
        for(int i = k; i >= 0; i--){
            int[] cur = new int[n];
            Arrays.fill(cur, INF);
            for(int[] flight : flights){
                cur[flight[1]] = Math.min(cur[flight[1]], cost[flight[0]] + flight[2]);
            }
            cost = cur;
            ans = Math.min(ans, cost[dst]);
        }
        return ans == INF ? -1 : ans;
    }

  int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int K) {
    constexpr int kInfCost = 1e9;
    vector<vector<int>> dp(K + 2, vector<int>(n, kInfCost));
    dp[0][src] = 0;
    
    for (int i = 1; i <= K + 1; ++i) {
      dp[i][src] = 0;
      for (const auto& p : flights)
          dp[i][p[1]] = min(dp[i][p[1]], dp[i-1][p[0]] + p[2]);    
    }
    
    return dp[K + 1][dst] >= kInfCost ? -1 : dp[K + 1][dst];
  }

C++ w/ space compression O(n)
  public int findCheapestPrice(int n, int[][] flights, int src, int dst, int K) {
    final int kInfCost = 1<<30;
    int[] cost = new int[n];
    Arrays.fill(cost, kInfCost);
    cost[src] = 0;
    
    for (int i = 0; i <= K; ++i) {
      int[] tmp = cost.clone();
      for(int[] p: flights)
        tmp[p[1]] = Math.min(tmp[p[1]], cost[p[0]] + p[2]);
      cost = tmp;
    }
    
    return cost[dst] >= kInfCost ? -1 : cost[dst];
  }


Solution 1: DFS
C++ w/o prunning TLE
C++ w/ prunning
public:
  int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int K) {
    g_.clear();  
    for (const auto& e : flights)
      g_[e[0]].emplace_back(e[1], e[2]);
    vector<int> visited(n, 0);
    visited[src] = 1;
    int ans = INT_MAX;
    dfs(src, dst, K + 1, 0, visited, ans);
    return ans == INT_MAX ? - 1 : ans;
  }
private:
  unordered_map<int, vector<pair<int,int>>> g_;
  
  void dfs(int src, int dst, int k, int cost, vector<int>& visited, int& ans) {
    if (src == dst) {
      ans = cost;
      return;
    }
    
    if (k == 0) return;    
    
    for (const auto& p : g_[src]) {
      if (visited[p.first]) continue; // do not visit the same city twice.
      if (cost + p.second > ans) continue; // IMPORTANT!!! prunning
      visited[p.first] = 1;
      dfs(p.first, dst, k - 1, cost + p.second, visited, ans);
      visited[p.first] = 0;
    }
  }

https://github.com/allaboutjst/airbnb/blob/master/README.md
Given a flight itinerary consisting of starting city, destination city, and ticket price (2d list) - find the optimal price flight path to get from start to destination. (A variation of Dynamic Programming Shortest Path)
        public int minCost(List<String> lines, String source, String target, int k) {
            if (lines.size() == 0 || k < 0) {
                return 0;
            }
            Map<String, Flight> nodes = new HashMap<>();
            for (String line : lines) {
                String[] s = line.trim().split(",");
                String[] t = s[0].trim().split("->");
                String from = t[0];
                String to = t[1];
                int cost = Integer.valueOf(s[1].trim());
                if (!nodes.containsKey(from)) nodes.put(from, new Flight(from));
                if (!nodes.containsKey(to)) nodes.put(to, new Flight(to));
                nodes.get(from).nextNodes.put(to, cost);
            }

            boolean find = false;
            Queue<String> q = new LinkedList<>();
            Queue<Integer> cost = new LinkedList<>();
            q.offer(source);
            cost.offer(0);
            int stops = -1;
            while (!q.isEmpty()) {
                stops++;
                if (stops > k + 1) {
                    break;
                }
                int qSize = q.size();
                for (int i = 0; i < qSize; i++) {
                    Flight curr = nodes.get(q.poll());
                    int currCost = cost.poll();
                    curr.minCost = Math.min(curr.minCost, currCost);

                    if (curr.name.equals(target)) {
                        find = true;
                        continue;
                    }

                    for (String next : curr.nextNodes.keySet()) {
                        int nextCost = currCost + curr.nextNodes.get(next);
                        if (nextCost < nodes.get(next).minCost && (stops < k || stops == k && next.equals(target))) {
                            q.offer(next);
                            cost.offer(nextCost);
                        }
                    }
                }
            }

            return find ? nodes.get(target).minCost : -1;
        }
    }

    class Flight {
        String name;
        int minCost;
        Map<String, Integer> nextNodes;

        Flight(String name) {
            this.name = name;
            this.minCost = Integer.MAX_VALUE;
            this.nextNodes = new HashMap<>();
        }
    }



at
Labels: , , , , , , , , ,

Labels

LeetCode (1432) GeeksforGeeks (1122) LeetCode - Review (1067) Review (882) Algorithm (668) to-do (609) Classic Algorithm (270) Google Interview (237) Classic Interview (222) Dynamic Programming (220) DP (186) Bit Algorithms (145) POJ (141) Math (137) Tree (132) LeetCode - Phone (129) EPI (122) Cracking Coding Interview (119) DFS (115) Difficult Algorithm (115) Lintcode (115) Different Solutions (110) Smart Algorithm (104) Binary Search (96) BFS (91) HackerRank (90) Binary Tree (86) Hard (79) Two Pointers (78) Stack (76) Company-Facebook (75) BST (72) Graph Algorithm (72) Time Complexity (69) Greedy Algorithm (68) Interval (63) Company - Google (62) Geometry Algorithm (61) Interview Corner (61) LeetCode - Extended (61) Union-Find (60) Trie (58) Advanced Data Structure (56) List (56) Priority Queue (53) Codility (52) ComProGuide (50) LeetCode Hard (50) Matrix (50) Bisection (48) Segment Tree (48) Sliding Window (48) USACO (46) Space Optimization (45) Company-Airbnb (41) Greedy (41) Mathematical Algorithm (41) Tree - Post-Order (41) ACM-ICPC (40) Algorithm Interview (40) Data Structure Design (40) Graph (40) Backtracking (39) Data Structure (39) Jobdu (39) Random (39) Codeforces (38) Knapsack (38) LeetCode - DP (38) Recursive Algorithm (38) String Algorithm (38) TopCoder (38) Sort (37) Introduction to Algorithms (36) Pre-Sort (36) Beauty of Programming (35) Must Known (34) Binary Search Tree (33) Follow Up (33) prismoskills (33) Palindrome (32) Permutation (31) Array (30) Google Code Jam (30) HDU (30) Array O(N) (29) Logic Thinking (29) Monotonic Stack (29) Puzzles (29) Code - Detail (27) Company-Zenefits (27) Microsoft 100 - July (27) Queue (27) Binary Indexed Trees (26) TreeMap (26) to-do-must (26) 1point3acres (25) GeeksQuiz (25) Merge Sort (25) Reverse Thinking (25) hihocoder (25) Company - LinkedIn (24) Hash (24) High Frequency (24) Summary (24) Divide and Conquer (23) Proof (23) Game Theory (22) Topological Sort (22) Lintcode - Review (21) Tree - Modification (21) Algorithm Game (20) CareerCup (20) Company - Twitter (20) DFS + Review (20) DP - Relation (20) Brain Teaser (19) DP - Tree (19) Left and Right Array (19) O(N) (19) Sweep Line (19) UVA (19) DP - Bit Masking (18) LeetCode - Thinking (18) KMP (17) LeetCode - TODO (17) Probabilities (17) Simulation (17) String Search (17) Codercareer (16) Company-Uber (16) Iterator (16) Number (16) O(1) Space (16) Shortest Path (16) itint5 (16) DFS+Cache (15) Dijkstra (15) Euclidean GCD (15) Heap (15) LeetCode - Hard (15) Majority (15) Number Theory (15) Rolling Hash (15) Tree Traversal (15) Brute Force (14) Bucket Sort (14) DP - Knapsack (14) DP - Probability (14) Difficult (14) Fast Power Algorithm (14) Pattern (14) Prefix Sum (14) TreeSet (14) Algorithm Videos (13) Amazon Interview (13) Basic Algorithm (13) Codechef (13) Combination (13) Computational Geometry (13) DP - Digit (13) LCA (13) LeetCode - DFS (13) Linked List (13) Long Increasing Sequence(LIS) (13) Math-Divisible (13) Reservoir Sampling (13) mitbbs (13) Algorithm - How To (12) Company - Microsoft (12) DP - Interval (12) DP - Multiple Relation (12) DP - Relation Optimization (12) LeetCode - Classic (12) Level Order Traversal (12) Prime (12) Pruning (12) Reconstruct Tree (12) Thinking (12) X Sum (12) AOJ (11) Bit Mask (11) Company-Snapchat (11) DP - Space Optimization (11) Dequeue (11) Graph DFS (11) MinMax (11) Miscs (11) Princeton (11) Quick Sort (11) Stack - Tree (11) 尺取法 (11) 挑战程序设计竞赛 (11) Coin Change (10) DFS+Backtracking (10) Facebook Hacker Cup (10) Fast Slow Pointers (10) HackerRank Easy (10) Interval Tree (10) Limited Range (10) Matrix - Traverse (10) Monotone Queue (10) SPOJ (10) Starting Point (10) States (10) Stock (10) Theory (10) Tutorialhorizon (10) Kadane - Extended (9) Mathblog (9) Max-Min Flow (9) Maze (9) Median (9) O(32N) (9) Quick Select (9) Stack Overflow (9) System Design (9) Tree - Conversion (9) Use XOR (9) Book Notes (8) Company-Amazon (8) DFS+BFS (8) DP - States (8) Expression (8) Longest Common Subsequence(LCS) (8) One Pass (8) Quadtrees (8) Traversal Once (8) Trie - Suffix (8) 穷竭搜索 (8) Algorithm Problem List (7) All Sub (7) Catalan Number (7) Cycle (7) DP - Cases (7) Facebook Interview (7) Fibonacci Numbers (7) Flood fill (7) Game Nim (7) Graph BFS (7) HackerRank Difficult (7) Hackerearth (7) Inversion (7) Kadane’s Algorithm (7) Manacher (7) Morris Traversal (7) Multiple Data Structures (7) Normalized Key (7) O(XN) (7) Radix Sort (7) Recursion (7) Sampling (7) Suffix Array (7) Tech-Queries (7) Tree - Serialization (7) Tree DP (7) Trie - Bit (7) 蓝桥杯 (7) Algorithm - Brain Teaser (6) BFS - Priority Queue (6) BFS - Unusual (6) Classic Data Structure Impl (6) DP - 2D (6) DP - Monotone Queue (6) DP - Unusual (6) DP-Space Optimization (6) Dutch Flag (6) How To (6) Interviewstreet (6) Knapsack - MultiplePack (6) Local MinMax (6) MST (6) Minimum Spanning Tree (6) Number - Reach (6) Parentheses (6) Pre-Sum (6) Probability (6) Programming Pearls (6) Rabin-Karp (6) Reverse (6) Scan from right (6) Schedule (6) Stream (6) Subset Sum (6) TSP (6) Xpost (6) n00tc0d3r (6) reddit (6) AI (5) Abbreviation (5) Anagram (5) Art Of Programming-July (5) Assumption (5) Bellman Ford (5) Big Data (5) Code - Solid (5) Code Kata (5) Codility-lessons (5) Coding (5) Company - WMware (5) Convex Hull (5) Crazyforcode (5) DFS - Multiple (5) DFS+DP (5) DP - Multi-Dimension (5) DP-Multiple Relation (5) Eulerian Cycle (5) Graph - Unusual (5) Graph Cycle (5) Hash Strategy (5) Immutability (5) Java (5) LogN (5) Manhattan Distance (5) Matrix Chain Multiplication (5) N Queens (5) Pre-Sort: Index (5) Quick Partition (5) Quora (5) Randomized Algorithms (5) Resources (5) Robot (5) SPFA(Shortest Path Faster Algorithm) (5) Shuffle (5) Sieve of Eratosthenes (5) Strongly Connected Components (5) Subarray Sum (5) Sudoku (5) Suffix Tree (5) Swap (5) Threaded (5) Tree - Creation (5) Warshall Floyd (5) Word Search (5) jiuzhang (5)

Popular Posts