Implement k stacks in a single array
Problem 2: How can you implement n (n > 2) stacks in a single array, where no stack overflows until no space left in the entire array space?
Let’s take three stacks sharing an array with capacity 10 as an example. Figure 3 shows the initial status for the array and stacks. Each item in the array has two blocks, one for item data and the other for the index of another block.
 |
| Figure 3: Initial status of three stacks sharing an array |
As shown in Figure 3, each item is linked to the next item (the link block of the ith item is i+1). The head of list for available items in the array points to the item at position 0, which is the Ava pointer in the figure. Since three stacks are empty, their top (Top1, Top2 and Top3 in the figure) are initialized as -1.
Let’s try to push an item a into the first stack. Currently the first available item is at the position 0, so we set its data block as a. The link block of the item is 1, which means the next available item is at the position 1, so we update the Ava pointer to the position 1. Additionally, the link block of the item at the position 1 should be updated to -1, the previous top index of the first stack. Lastly, we update to top index of the first stack to 0. The status of the array and stacks are shown in Figure 4.
 |
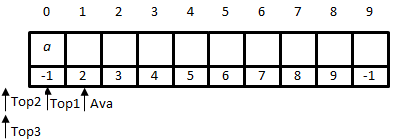| Figure 4: The status after pushing a into the first stack |
Let’s push two more items b and c into the first stack. The operations are similar as before, and the status is shown in Figure 5.
 |
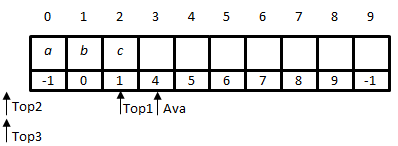| Figure 5: The status after adding two more items, b and c, into the first stack |
In the next step we are going to push another d into the second stack. Most operations are similar as before. The link block in the item at the position 3 is updated to -1, since the second stack is empty before and its top index is -1 previously. And then the top index of the second stack is updated to 3. The status after adding d into the second stack is shown in Figure 6.
 |
| Figure 6: The status after pushing d into the second stack |
If we continue to push three more item e, f, and g into the second stack, the status is shown in Figure 7.
 |
| Figure 7: The status after pushing three more items, e, f, and g, into the second stack |
At this time we are going to pop an item from the first stack. Since the top index of the first stack is 2, the item to be popped off is at the position 2. The link value in that item is 1, which means the previous top in the first stack is at the position 1 in the array, so we update the top index of the first stack as 1. Now the item at the position 2 becomes available, it should be linked to the list for available items. We move the Ava pointer to 2, and then update the link value of the item at the position 2 as 7, which is the previous head position of the list for available items. The status is shown in Figure 8.
 |
| Figure 8: The status after popping an item from the first stack |
If we pop an item off the second stack, the item at the position 6 will be linked to the list for available items too. Figure 9 depicts the status after the related operations.
 |
| Figure 9: The status after popping an item off the second stack |
If we push h into the third stack, it will be placed into the item at the position 6 because Ava points to that item. The next available item is at the position 2 (the link value in the item at the position 6). Therefore, the head of the list for available items points to location 2, as shown in Figure 10.
 |
| Figure 10: The status after pushing h into the third stack |
Let’s continue to push four more items into the third stack, i, j, k, and l. The status after these four items are pushed is shown in Figure 11. At this time, there are two items in the first stack (a and b), three items in the second stack (d, e and f), and five items in the third stack (h, i, j, k, and l). Please note that items inside a stack are not necessarily adjacent.
 |
| Figure 11: The status after pushing i, j, k, l into the third stack |
After l is pushed into the item at the position 9, the Ava pointer is update to -1 (the previous link value in the item at the position 9), which means all items in the array have been occupied by stacks. We can’t push more items until some items are popped off.
template <typename T, int capacity, int count> class Stacks
{
public:
Stacks()
{
int i;
for(i = 0; i < capacity - 1; ++i)
items[i].link = i + 1;
items[i].link = -1;
emptyHead = 0;
for(i = 0; i < count; ++i)
stackHead[i] = -1;
}
T top(int stackIndex)
{
validateIndex(stackIndex);
if(empty(stackIndex))
throw new exception("The stack is empty.");
return items[stackHead[stackIndex]].data;
}
void push(int stackIndex, const T& item)
{
validateIndex(stackIndex);
if(full())
throw new exception("All space has been occupied.");
Item<T>& block = items[emptyHead];
int nextEmpty = block.link;
block.data = item;
block.link = stackHead[stackIndex];
stackHead[stackIndex] = emptyHead;
emptyHead = nextEmpty;
}
void pop(int stackIndex)
{
validateIndex(stackIndex);
if(empty(stackIndex))
throw new exception("The stack is empty.");
Item<T>& block = items[stackHead[stackIndex]];
int nextItem = block.link;
block.link = emptyHead;
emptyHead = stackHead[stackIndex];
stackHead[stackIndex] = nextItem;emptyHead = stackHead[stackIndex];
}
bool empty(int stackIndex)
{
return (stackHead[stackIndex] < 0);
}
private:
void validateIndex(int stackIndex)
{
if(stackIndex < 0 || stackIndex >= count)
throw new exception("Invalid index of stack.");
}
bool full()
{
return (emptyHead < 0);
}
private:
template <typename T> struct Item
{
T data;
int link;
};
private:
Item<T> items[capacity];
int emptyHead;
int stackHead[count];
};
Create a data structure kStacks that represents k stacks. Implementation of kStacks should use only one array, i.e., k stacks should use the same array for storing elements.
Following functions must be supported by kStacks.
push(int x, int sn) –> pushes x to stack number ‘sn’ where sn is from 0 to k-1
pop(int sn) –> pops an element from stack number ‘sn’ where sn is from 0 to k-1
pop(int sn) –> pops an element from stack number ‘sn’ where sn is from 0 to k-1
Method 2 (A space efficient implementation)
The idea is to use two extra arrays for efficient implementation of k stacks in an array. This may not make much sense for integer stacks, but stack items can be large for example stacks of employees, students, etc where every item is of hundreds of bytes. For such large stacks, the extra space used is comparatively very less as we use two integer arrays as extra space.
The idea is to use two extra arrays for efficient implementation of k stacks in an array. This may not make much sense for integer stacks, but stack items can be large for example stacks of employees, students, etc where every item is of hundreds of bytes. For such large stacks, the extra space used is comparatively very less as we use two integer arrays as extra space.
Following are the two extra arrays are used:
1) top[]: This is of size k and stores indexes of top elements in all stacks.
2) next[]: This is of size n and stores indexes of next item for the items in array arr[]. Here arr[] is actual array that stores k stacks.
Together with k stacks, a stack of free slots in arr[] is also maintained. The top of this stack is stored in a variable ‘free’.
1) top[]: This is of size k and stores indexes of top elements in all stacks.
2) next[]: This is of size n and stores indexes of next item for the items in array arr[]. Here arr[] is actual array that stores k stacks.
Together with k stacks, a stack of free slots in arr[] is also maintained. The top of this stack is stored in a variable ‘free’.
All entries in top[] are initialized as -1 to indicate that all stacks are empty. All entries next[i] are initialized as i+1 because all slots are free initially and pointing to next slot. Top of free stack, ‘free’ is initialized as 0.
The best part of above implementation is, if there is a slot available in stack, then an item can be pushed in any of the stacks, i.e., no wastage of space.
https://www.byte-by-byte.com/nstacks/
public class Stacks {
int[] topOfStack;
int[] stackData;
int[] nextIndex;
int nextAvailable = 0;
public Stacks(int numStacks, int capacity) {
topOfStack = new int[numStacks];
for (int i = 0; i < topOfStack.length; i++) {
topOfStack[i] = -1;
}
stackData = new int[capacity];
nextIndex = new int[capacity];
for (int i = 0; i < nextIndex.length - 1; i++) {
nextIndex[i] = i+1;
}
nextIndex[nextIndex.length - 1] = -1;
}
public void push(int stack, int value) {
if (stack < 0 || stack >= topOfStack.length) {
throw new IndexOutOfBoundsException();
}
if (nextAvailable < 0) return;
int currentIndex = nextAvailable;
nextAvailable = nextIndex[currentIndex];
stackData[currentIndex] = value;
nextIndex[currentIndex] = topOfStack[stack];
topOfStack[stack] = currentIndex;
}
public int pop(int stack) {
if (stack < 0 || stack >= topOfStack.length
|| topOfStack[stack] < 0) {
throw new IndexOutOfBoundsException();
}
int currentIndex = topOfStack[stack];
int value = stackData[currentIndex];
topOfStack[stack] = nextIndex[currentIndex];
nextIndex[currentIndex] = nextAvailable;
nextAvailable = currentIndex;
return value;
}
}
Method 1 (Divide the array in slots of size n/k)
A simple way to implement k stacks is to divide the array in k slots of size n/k each, and fix the slots for different stacks, i.e., use arr[0] to arr[n/k-1] for first stack, and arr[n/k] to arr[2n/k-1] for stack2 where arr[] is the array to be used to implement two stacks and size of array be n.
A simple way to implement k stacks is to divide the array in k slots of size n/k each, and fix the slots for different stacks, i.e., use arr[0] to arr[n/k-1] for first stack, and arr[n/k] to arr[2n/k-1] for stack2 where arr[] is the array to be used to implement two stacks and size of array be n.
The problem with this method is inefficient use of array space. A stack push operation may result in stack overflow even if there is space available in arr[].
Describe how you could use a single array to implement three stacks.https://hellosmallworld123.wordpress.com/2014/05/09/describe-how-you-could-use-a-single-array-to-implement-three-stacks/
The other solution is to use a pointer to keep track of the previous location for every entry. The user can add elements as long as there is free space in the array. We also need to have a free list to keep track of all the free elements that was popped. So first we add all the elements into the free list. we can only use integer to track the head of the stacks.
public class Stack { int STACKSIZE = 300; int [] head = {-1, -1, -1}; StackNode [] s = new StackNode[STACKSIZE]; int [] free = new int [STACKSIZE]; int firstFree = 0; public Stack() { for (int i = 0; i < STACKSIZE; i++) { free[i] = i; } } public boolean push(int stackNum, int val) { if (firstFree == STACKSIZE) return false; //no space to push s[free[firstFree]] = new StackNode(val); s[free[firstFree]].pre = head[stackNum]; head[stackNum] = free[firstFree]; firstFree++; return true; } public int pop(int stackNum) { if (head[stackNum] == -1) return -1; // empty stack StackNode n = s[head[stackNum]]; firstFree--; free[firstFree] = head[stackNum]; // add to freelist head[stackNum] = n.pre; return n.val; } public int peek(int stackNum) { if (head[stackNum] == -1) return -1; //empty stack return s[head[stackNum]].val; }}public class StackNode { int val; int pre; // only track the previous index, not the node itself public StackNode (int v) { this.val = v; }}https://github.com/wzhishen/cracking-the-coding-interview/blob/master/src/chap03/Q1.java
Not good: space wasted.
public class Q1 {
//Describe how you could use a single array to implement three stacks.
final int STACK_SIZE = 100;
int[] buffer = new int[3 * STACK_SIZE];
int[] stackPointer = {-1, -1, -1}; // relative index
void push(int stackNum, int x) {
if (isFull(stackNum))
throw new IllegalArgumentException("Stack is full!");
++stackPointer[stackNum];
buffer[getAbsIndex(stackNum)] = x;
}
int pop(int stackNum) {
int ret = peek(stackNum);
--stackPointer[stackNum];
return ret;
}
int peek(int stackNum) {
if (isEmpty(stackNum))
throw new IllegalArgumentException("Stack is empty!");
return buffer[getAbsIndex(stackNum)];
}
boolean isEmpty(int stackNum) {
return stackPointer[stackNum] == -1;
}
boolean isFull(int stackNum) {
return stackPointer[stackNum] == STACK_SIZE - 1;
}
private int getAbsIndex(int stackNum) {
return stackNum * STACK_SIZE + stackPointer[stackNum];
}
Read full article from How to efficiently implement k stacks in a single array? - GeeksforGeeks
