https://community.topcoder.com/stat?c=problem_statement&pm=2940&rd=5854
http://www.hawstein.com/posts/dp-novice-to-advanced.html


http://blog.gogo244.tw/2015/07/30/topcoder-srm-208-div1-staradventure/
The latest version of your favorite adventure game has just been released. On each level you search for stars that earn you points. Simply moving over a location containing stars allows you to acquire them. To help you on your journey, you are given an overhead map of the level in a String[]. Each character in level describes the number of stars at that location. You begin in the upper left spot of the map (character 0 of element 0 of level). On the current stage you must move according to the following rules:
|
http://www.hawstein.com/posts/dp-novice-to-advanced.html
给定一个M行N列的矩阵(M*N个格子),每个格子中放着一定数量的苹果。 你从左上角的格子开始,只能向下或向右走,目的地是右下角的格子。 你每走过一个格子,就把格子上的苹果都收集起来。然后你从右下角走回左上角的格子, 每次只能向左或是向上走,同样的,走过一个格子就把里面的苹果都收集起来。 最后,你再一次从左上角走到右下角,每过一个格子同样要收集起里面的苹果 (如果格子里的苹果数为0,就不用收集)。求你最多能收集到多少苹果。
注意:当你经过一个格子时,你要一次性把格子里的苹果都拿走。
限制条件:1 < N, M <= 50;每个格子里的苹果数量是0到1000(包含0和1000)。
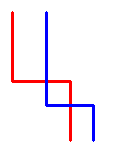
如果我们只需要从左上角的格子走到右下角的格子一次,并且收集最大数量的苹果, 那么问题就退化为“中级”一节里的那个问题。将这里的问题规约为“中级”里的简单题, 这样一来会比较好解。让我们来分析一下这个问题,要如何规约或是修改才能用上DP。 首先,对于第二次从右下角走到左上角得出的这条路径, 我们可以将它视为从左上角走到右下角得出的路径,没有任何的差别。 (即从B走到A的最优路径和从A走到B的最优路径是一样的)通过这种方式, 我们得到了三条从顶走到底的路径。对于这一点的理解可以稍微减小问题的难度。 于是,我们可以将这3条路径记为左,中,右路径。对于两条相交路径(如下图):
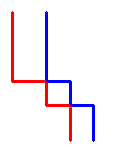
在不影响结果的情况下,我们可以将它们视为两条不相交的路径:
这样一来,我们将得到左,中,右3条路径。此外,如果我们要得到最优解, 路径之间不能相交(除了左上角和右下角必然会相交的格子)。因此对于每一行y( 除了第一行和最后一行),三条路径对应的x坐标要满足:x1[y] < x2[y] < x3[y]。 经过这一步的分析,问题的DP解法就进一步地清晰了。让我们考虑行y, 对于每一个x1[y-1],x2[y-1]和x3[y-1],我们已经找到了能收集到最多苹果数量的路径。 根据它们,我们能求出行y的最优解。现在我们要做的就是找到从一行移动到下一行的方式。 令Max[i][j][k]表示到第y-1行为止收集到苹果的最大数量, 其中3条路径分别止于第i,j,k列。对于下一行y,对每个Max[i][j][k] 都加上格子(y,i),(y,j)和(y,k)内的苹果数量。因此,每一步我们都向下移动。 我们做了这一步移动之后,还要考虑到,一条路径是有可能向右移动的。 (对于每一个格子,我们有可能是从它上面向下移动到它, 也可能是从它左边向右移动到它)。为了保证3条路径互不相交, 我们首先要考虑左边的路径向右移动的情况,然后是中间,最后是右边的路径。 为了更好的理解,让我们来考虑左边的路径向右移动的情况,对于每一个可能的j,k对(j<k), 对每个i(i<j),考虑从位置(i-1,j,k)移动到位置(i,j,k)。处理完左边的路径, 再处理中间的路径,最后处理右边的路径。方法都差不多。
https://www.topcoder.com/community/competitive-programming/tutorials/dynamic-programming-from-novice-to-advanced/
Given a matrix with M rows and N columns (N x M). In each cell there’s a number of apples.
You start from the upper-left corner of the matrix. You can go down or right one cell. You need to arrive to the bottom-right corner. Then you need to go back to the upper-left cell by going each step one cell left or up. Having arrived at this upper-left cell, you need to go again back to the bottom-right cell.
Find the maximum number of apples you can collect.
When you pass through a cell – you collect all the apples left there.
You start from the upper-left corner of the matrix. You can go down or right one cell. You need to arrive to the bottom-right corner. Then you need to go back to the upper-left cell by going each step one cell left or up. Having arrived at this upper-left cell, you need to go again back to the bottom-right cell.
Find the maximum number of apples you can collect.
When you pass through a cell – you collect all the apples left there.
Restrictions: 1 < N, M <= 50 ; each cell contains between 0 and 1000 apples inclusive.
First of all we observe that this problem resembles to the classical one (described in Section 3 of this article), in which you need to go only once from the top-left cell to the bottom-right one, collecting the maximum possible number of apples. It would be better to try to reduce the problem to this one. Take a good look into the statement of the problem – what can be reduced or modified in a certain way to make it possible to solve using DP? First observation is that we can consider the second path (going from bottom-right cell to the top-left cell) as a path which goes from top-left to bottom-right cell. It makes no difference, because a path passed from bottom to top, may be passed from top to bottom just in reverse order. In this way we get three paths going from top to bottom. This somehow decreases the difficulty of the problem. We can consider these 3 paths as left, middle and right. When 2 paths intersect (like in the figure below)
First of all we observe that this problem resembles to the classical one (described in Section 3 of this article), in which you need to go only once from the top-left cell to the bottom-right one, collecting the maximum possible number of apples. It would be better to try to reduce the problem to this one. Take a good look into the statement of the problem – what can be reduced or modified in a certain way to make it possible to solve using DP? First observation is that we can consider the second path (going from bottom-right cell to the top-left cell) as a path which goes from top-left to bottom-right cell. It makes no difference, because a path passed from bottom to top, may be passed from top to bottom just in reverse order. In this way we get three paths going from top to bottom. This somehow decreases the difficulty of the problem. We can consider these 3 paths as left, middle and right. When 2 paths intersect (like in the figure below)

we may consider them as in the following picture, without affecting the result:

This way we’ll get 3 paths, which we may consider as being one left, one middle and the other – right. More than that, we may see that for getting an optimal results they must not intersect (except in the leftmost upper corner and rightmost bottom corner). So for each row y (except first and last), the x coordinates of the lines (x1[y] , x2[y] and respectively x3[y] ) will be : x1[y] < x2[y] < x3[y] . Having done that – the DP solution now becomes much clearer. Let’s consider the row y. Now suppose that for any configuration of x1[y-1] , x2[y-1] and x3[y-1] we have already found the paths which collect the maximum number of apples. From them we can find the optimal solution for row y. We now have to find only the way for passing from one row to the next one. Let Max[i][j][k] represent the maximum number of apples collected till row y-1inclusive, with three paths finishing at column i, j, and respectively k. For the next row y, add to each Max[i][j][k] (obtained previously) the number of apples situated in cells (y,i) , (y,j) and (y,k). Thus we move down at each step. After we made such a move, we must consider that the paths may move in a row to the right. For keeping the paths out of an intersection, we must first consider the move to the right of the left path, after this of the middle path, and then of the right path. For a better understanding think about the move to the right of the left path – take every possible pair of, k (where j<k), and for each i (1 i<j) consider the move from position (i-1,j,k) to position (i,j,k). Having done this for the left path, start processing the middle one, which is done similarly; and then process the right path.
https://github.com/gabesoft/topc/blob/master/src.archive.1/dynamic/StarAdventure.java
int N;
int M;
int[][] data;
int[][][] best;
int[][][] sums;
public int mostStars(String[] level) {
N = level.length;
M = level[0].length();
data = new int[N][M];
sums = new int[N][M][M];
for (int i = 0; i < N; i++) {
char[] chars = level[i].toCharArray();
for (int j = 0; j < M; j++) {
data[i][j] = chars[j] - '0';
}
}
computeSums();
if (M <= 3) { return sumAll(); }
best = new int[M][M][M];
for (int y = 0; y < N; y++) {
int[][][] curr = new int[M][M][M];
for (int i = 0; i < M - 2; i++) {
for (int j = i + 1; j < M - 1; j++) {
for (int k = j + 1; k < M; k++) {
curr[i][j][k] = findBest(y, i, j, k);
}
}
}
best = curr;
}
return best[M - 3][M - 2][M - 1];
}
int findBest(int row, int i, int j, int k) {
int curr = 0;
for (int ip = 0; ip < i + 1; ip++) {
for (int jp = i + 1; jp < j + 1; jp++) {
for (int kp = j + 1; kp < k + 1; kp++) {
curr = Math.max(curr, best[ip][jp][kp] + sums[row][ip][i] + sums[row][jp][j] + sums[row][kp][k]);
}
}
}
return curr;
}
void computeSums() {
for (int y = 0; y < N; y++) {
for (int i = 0; i < M; i++) {
for (int j = i; j < M; j++) {
sums[y][i][j] = sum(y, i, j);
}
}
}
}
int sum(int row, int start, int end) {
int res = 0;
for (int i = start; i < end + 1; i++) { res += data[row][i]; }
return res;
}
int sumAll() {
int res = 0;
for (int i = 0; i < N; i++) { res += sums[i][0][M - 1]; }
return res;
}
int N;
int M;
int[][] data;
int[][][] best;
int[][][] sums;
public int mostStars(String[] level) {
N = level.length;
M = level[0].length();
data = new int[N][M];
sums = new int[N][M][M];
for (int i = 0; i < N; i++) {
char[] chars = level[i].toCharArray();
for (int j = 0; j < M; j++) {
data[i][j] = chars[j] - '0';
}
}
computeSums();
if (M <= 3) { return sumAll(); }
best = new int[M][M][M];
for (int y = 0; y < N; y++) {
int[][][] curr = new int[M][M][M];
for (int i = 0; i < M - 2; i++) {
for (int j = i + 1; j < M - 1; j++) {
for (int k = j + 1; k < M; k++) {
curr[i][j][k] = findBest(y, i, j, k);
}
}
}
best = curr;
}
return best[M - 3][M - 2][M - 1];
}
int findBest(int row, int i, int j, int k) {
int curr = 0;
for (int ip = 0; ip < i + 1; ip++) {
for (int jp = i + 1; jp < j + 1; jp++) {
for (int kp = j + 1; kp < k + 1; kp++) {
curr = Math.max(curr, best[ip][jp][kp] + sums[row][ip][i] + sums[row][jp][j] + sums[row][kp][k]);
}
}
}
return curr;
}
void computeSums() {
for (int y = 0; y < N; y++) {
for (int i = 0; i < M; i++) {
for (int j = i; j < M; j++) {
sums[y][i][j] = sum(y, i, j);
}
}
}
}
int sum(int row, int start, int end) {
int res = 0;
for (int i = start; i < end + 1; i++) { res += data[row][i]; }
return res;
}
int sumAll() {
int res = 0;
for (int i = 0; i < N; i++) { res += sums[i][0][M - 1]; }
return res;
}
public int mostStars(String[] level) { int row = level.length; int col = level[0].length(); int[][] map = new int[row][col]; int total = 0; for (int i=0; i<row; i++) { for (int j=0; j<col; j++) { map[i][j] = level[i].charAt(j) - '0'; total += map[i][j]; } } if (col < 4 || row < 4) { return total; } int[][][][] max = new int[row][col-2][col-1][col]; for (int r=0; r<row; r++) { for (int i=0; i<col-2; i++) { for (int j=i+1; j<col-1; j++) { for (int k=j+1; k<col; k++) { if (r == 0) { for (int l=0; l<=k; l++) { max[r][i][j][k] += map[0][l]; } } else { // Find the max for max[r][i][j][k] form max[r-1]... int maxp = 0; for (int ii=0; ii<=i; ii++) { for (int jj=ii+1; jj<=j; jj++) { for (int kk=jj+1; kk<=k; kk++) { int tmp = max[r-1][ii][jj][kk]; if (ii < i) { // Add move for (int a=ii; a<i; a++) { tmp += map[r][a]; } } tmp += map[r][i]; if (jj < j) { for (int b=jj; b<j; b++) { // Avoid duplicate add if (b > i) { tmp += map[r][b]; } } } tmp += map[r][j]; if (kk < k) { for (int c=kk; c<k; c++) { // Avoid duplicate add if (c > j) { tmp += map[r][c]; } } } tmp += map[r][k]; if (tmp > maxp) { maxp = tmp; } } } } max[r][i][j][k] = maxp; } } } } } // debug /* for (int i=0; i<col-2; i++) { for (int j=i+1; j<col-1; j++) { for (int k=j+1; k<col; k++) { System.out.printf("max[0][%d][%d][%d] = %d%n", i, j, k, max[0][i][j][k]); } } } for (int i=0; i<col-2; i++) { for (int j=i+1; j<col-1; j++) { for (int k=j+1; k<col; k++) { System.out.printf("max[1][%d][%d][%d] = %d%n", i, j, k, max[1][i][j][k]); } } } */ return max[row-1][col-3][col-2][col-1]; }