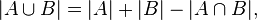HDU 4135-Co-prime - Inclusion–exclusion principle

http://www.cnblogs.com/UniqueColor/p/4733546.html

Given a number N, you are asked to count the number of integers between A and B inclusive which are relatively prime to N. Two integers are said to be co-prime or relatively prime if they have no common positive divisors other than 1 or, equivalently, if their greatest common divisor is 1. The number 1 is relatively prime to every integer.

 

Input

The first line on input contains T (0 < T <= 100) the number of test cases, each of the next T lines contains three integers A, B, N where (1 <= A <= B <= 10¹⁵) and (1 <=N <= 10⁹).

 

Output

For each test case, print the number of integers between A and B inclusive which are relatively prime to N. Follow the output format below.

http://www.acmerblog.com/hdu-4135-co-prime-7138.html

03	typedef long long LL;

04

LL a,b;

05

int n;

06	LL tol,ans;

07	void dfs(int s,LL mul,int t)

08

{

09	if(s==cnt){

10	if(t) ans=ans+tol/mul;

11	else ans=ans-tol/mul;

12

return;

13

}

14	dfs(s+1,mul,t);

15	dfs(s+1,mul*f[s],1-t);

16

}

17	LL cal(LL x)

18

{

19	if(x==0) return 0;

20

tol=x;

21

ans=0;

22	dfs(0,1,1);

23	return ans;

24

}

25	int main()

26

{

27	// freopen("1.in","r",stdin);

28	int T,ca=0;

29	scanf("%d",&T);

30	while(T--){

31	scanf("%I64d%I64d%d",&a,&b,&n);

32	if(n==1) { printf("Case #%d: %I64d\n",++ca,b-a+1);continue;}

33

cnt=0;

34	for(int j=2;j*j<=n;j++){

35	if(n%j==0){

36	f[cnt++]=j;

37	while(n%j==0) n/=j;

38

}

39

}

40	if(n>1) f[cnt++]=n;

41

42	// for(int i=0;i<cnt;i++) printf("%d\n",f[i]);

43	printf("Case #%d: %I64d\n",++ca,cal(b)-cal(a-1));

44

}

45

}

Inclusion–exclusion principle
https://en.wikipedia.org/wiki/Inclusion%E2%80%93exclusion_principle

In combinatorics (combinatorial mathematics), the inclusion–exclusion principle is a counting technique which generalizes the familiar method of obtaining the number of elements in the union of two finite sets; symbolically expressed as

where A and B are two finite sets and |S| indicates the cardinality of a set S (which may be considered as the number of elements of the set, if the set is finite). The formula expresses the fact that the sum of the sizes of the two sets may be too large since some elements may be counted twice. The double-counted elements are those in the intersection of the two sets and the count is corrected by subtracting the size of the intersection.

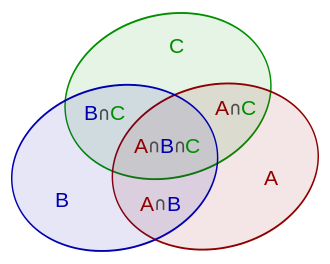
The principle is more clearly seen in the case of three sets, which for the sets A, B and C is given by

Generalizing the results of these examples gives the principle of inclusion–exclusion. To find the cardinality of the union of n sets:

1. Include the cardinalities of the sets.
2. Exclude the cardinalities of the pairwise intersections.
3. Include the cardinalities of the triple-wise intersections.
4. Exclude the cardinalities of the quadruple-wise intersections.
5. Include the cardinalities of the quintuple-wise intersections.
6. Continue, until the cardinality of the n-tuple-wise intersection is included (if n is odd) or excluded (n even).