https://codility.com/programmers/lessons/8
the function should return 3, as explained above.
A non-empty zero-indexed array A consisting of N integers is given.
A peak is an array element which is larger than its neighbours. More precisely, it is an index P such that 0 < P < N − 1 and A[P − 1] < A[P] > A[P + 1].
For example, the following array A:
A[0] = 1
A[1] = 5
A[2] = 3
A[3] = 4
A[4] = 3
A[5] = 4
A[6] = 1
A[7] = 2
A[8] = 3
A[9] = 4
A[10] = 6
A[11] = 2
has exactly four peaks: elements 1, 3, 5 and 10.
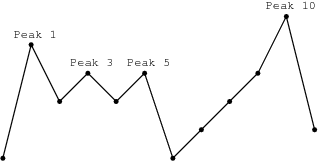
You are going on a trip to a range of mountains whose relative heights are represented by array A, as shown in a figure below. You have to choose how many flags you should take with you. The goal is to set the maximum number of flags on the peaks, according to certain rules.

Flags can only be set on peaks. What's more, if you take K flags, then the distance between any two flags should be greater than or equal to K. The distance between indices P and Q is the absolute value |P − Q|.
For example, given the mountain range represented by array A, above, with N = 12, if you take:
- two flags, you can set them on peaks 1 and 5;
- three flags, you can set them on peaks 1, 5 and 10;
- four flags, you can set only three flags, on peaks 1, 5 and 10.
You can therefore set a maximum of three flags in this case.
Write a function:
int solution(int A[], int N);
that, given a non-empty zero-indexed array A of N integers, returns the maximum number of flags that can be set on the peaks of the array.
For example, the following array A:
A[0] = 1
A[1] = 5
A[2] = 3
A[3] = 4
A[4] = 3
A[5] = 4
A[6] = 1
A[7] = 2
A[8] = 3
A[9] = 4
A[10] = 6
A[11] = 2
the function should return 3, as explained above.
First of all, instead of retaining the indices of the peeks as above solutions, we create an array that holds the next peek on the right side of the array at each index.
int solution(int A[], int N) {
//for N < 3, there can be no peak.
if (N < 3){
return 0;
}
int* next_peek = (int*)alloca(sizeof(int) * N);
//-1 stands for there is no more peek.
next_peek[N - 1] = -1;
//scan backwards
int peek_cnt = 0;
int i;
for (i = N - 2; i > 0; i--){
if (A[i - 1] < A[i] && A[i] > A[i + 1]){
next_peek[i] = i;
peek_cnt++;
}
else {
next_peek[i] = next_peek[i + 1];
}
}
next_peek[0] = next_peek[1];
//now let's check
int max_flags = 0;
for (i = 1; (i - 1) * i + 2 < N && i <= peek_cnt; i++){
int pos = 0;
int num = 0;
while (pos < N && num < i){
pos = next_peek[pos];
//we don't have any more peek. exit this loop.
if (pos == -1){
break;
}
//we can set a flag at the pos.
//increment pos to seek the next peek
num++;
pos += i;
}
max_flags = max_flags < num ? num : max_flags;
}
return max_flags;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
|
def solution(A):
from math import sqrt
A_len = len(A)
next_peak = [-1] * A_len
peaks_count = 0
first_peak = -1
# Generate the information, where the next peak is.
for index in xrange(A_len-2, 0, -1):
if A[index] > A[index+1] and A[index] > A[index-1]:
next_peak[index] = index
peaks_count += 1
first_peak = index
else:
next_peak[index] = next_peak[index+1]
if peaks_count < 2:
# There is no peak or only one.
return peaks_count
max_flags = 1
max_min_distance = int(sqrt(A_len))
for min_distance in xrange(max_min_distance + 1, 1, -1):
# Try for every possible distance.
flags_used = 1
flags_have = min_distance-1 # Use one flag at the first peak
pos = first_peak
while flags_have > 0:
if pos + min_distance >= A_len-1:
# Reach or beyond the end of the array
break
pos = next_peak[pos+min_distance]
if pos == -1:
# No peak available afterward
break
flags_used += 1
flags_have -= 1
max_flags = max(max_flags, flags_used)
return max_flags
|
http://codility-lessons.blogspot.com/2015/03/lesson-8-flags.html
Then, this leeds to the conclusion; as long as we can always start from the 1st peek and then pick up the nearest peek that satisfies the given constraint, it is enough to check if k flags can be set or not.
While this code gives the 100% correctness score, the performance score is obviously bad.
int check(int k, int* peeks, int peek_cnt)
int check(int k, int* peeks, int peek_cnt)
{
https://github.com/nkatre/Codility/blob/master/Hard/Peak%20and%20Flags%20(boron2013)
find the peak array first
use binary to find the flag number, start = 1, end = array.size(). make flag = (start + end) / 2;
time O( nlgn).
tips: pay attention to sf and ef , used flag
public int solution(int[] A) {
ArrayList<Integer> array = new ArrayList<Integer>();
for (int i = 1; i < A.length - 1; i++) {
if (A[i - 1] < A[i] && A[i + 1] < A[i]) {
array.add(i);
}
}
if (array.size() == 1 || array.size() == 0) {
return array.size();
}
int sf = 1;
int ef = array.size();
int result = 1;
while (sf <= ef) {
int flag = (sf + ef) / 2;
boolean suc = false;
int used = 0;
int mark = array.get(0);
for (int i = 0; i < array.size(); i++) {
if (array.get(i) >= mark) {
used++;
mark = array.get(i) + flag;
if (used == flag) {
suc = true;
break;
}
}
}
if (suc) {
result = flag;
sf = flag + 1;
} else {
ef = flag - 1;
}
}
return result;
}
http://blog.csdn.net/liushuying668/article/details/38272157
思路:1.首先建一个N元容器B,用以存储peak的信息。(若第i个元素是peak,则B[i]=1,否则为0)
Notice that for every index i we cannot take more than i flags and set more than N i + 1 flags. We can take a maximum of O( √ N) flags, and the position of each of them can be found in a constant time, so the total number of operations does not exceed O(N + 1+ 2+. . .+ √ N) = O(N + √ N ^2 ) = O(N).
http://codesays.com/2014/solution-to-boron2013-flags-by-codility/
//if we have to put only one flag, it is always possible..
if (k == 1){
return 1;
}
//the first flag can be set.
int prev = peeks[0];
int rest = k - 1;
//check if this is true
int i = 1;
while (i < peek_cnt){
int curr = peeks[i];
if (curr - prev >= k){
prev = curr;
rest--;
//we consumed the all the flag.
if (rest == 0){
return 1;
}
}
i++;
}
return 0;
}
int solution(int A[], int N)
{
//the max number of the peeks is less than N / 2.
int* peeks = (int*)alloca(sizeof(int) * (N / 2) );
int peek_cnt = 0;
//let's find the peeks first.
int i;
for (i = 1; i < N - 1; i++){
if (A[i - 1] < A[i] && A[i] > A[i + 1]){
peeks[peek_cnt] = i;
peek_cnt++;
}
}
//we don't have to check when there is no peek found.
if (peek_cnt == 0){
return 0;
}
//check how many flags can be set...
int max_flags = 0;
for (int i = peek_cnt; i > 0; i--){
int ret = check(i, peeks, peek_cnt);
if (ret != 0){
max_flags = i;
break;
}
}
return max_flags;
}
https://github.com/nkatre/Codility/blob/master/Hard/Peak%20and%20Flags%20(boron2013)
find the peak array first
use binary to find the flag number, start = 1, end = array.size(). make flag = (start + end) / 2;
time O( nlgn).
tips: pay attention to sf and ef , used flag
public int solution(int[] A) {
ArrayList<Integer> array = new ArrayList<Integer>();
for (int i = 1; i < A.length - 1; i++) {
if (A[i - 1] < A[i] && A[i + 1] < A[i]) {
array.add(i);
}
}
if (array.size() == 1 || array.size() == 0) {
return array.size();
}
int sf = 1;
int ef = array.size();
int result = 1;
while (sf <= ef) {
int flag = (sf + ef) / 2;
boolean suc = false;
int used = 0;
int mark = array.get(0);
for (int i = 0; i < array.size(); i++) {
if (array.get(i) >= mark) {
used++;
mark = array.get(i) + flag;
if (used == flag) {
suc = true;
break;
}
}
}
if (suc) {
result = flag;
sf = flag + 1;
} else {
ef = flag - 1;
}
}
return result;
}
http://blog.csdn.net/liushuying668/article/details/38272157
思路:1.首先建一个N元容器B,用以存储peak的信息。(若第i个元素是peak,则B[i]=1,否则为0)
2.建立一个N元容器C,用以存储第i个元素的下一个peak元素下标。若第i个元素本身就是peak,则C[i]=i,否则C[i]=C[i+1],令C[N-1]=-1
3.由题设可知若有k个flag,则每相邻两个flag之间距离要大于等于k,由于首尾元素均不为peak,故k(k-1)+2<=N,可得k<=floor(sqrt(N))+1
故外层循环:i从1到sqrt(N)+1;令pos表示当前元素下标,num表示内层迭代次数也即flag数,内层循环:pos<N,num<i,先找到一个
peak,即令pos=C[pos],若C[pos]不等于-1,说明当前位置之后仍有peak存在,故pos+=i(flag间隔为i),num++,C[pos]等于-1说明当
前位置之后(含当前位置)无peak存在,跳出内层循环。
用res记录多次迭代中num的最大值,则res就是最大可能的flag数
Notice that for every index i we cannot take more than i flags and set more than N i + 1 flags. We can take a maximum of O( √ N) flags, and the position of each of them can be found in a constant time, so the total number of operations does not exceed O(N + 1+ 2+. . .+ √ N) = O(N + √ N ^2 ) = O(N).
http://codesays.com/2014/solution-to-boron2013-flags-by-codility/
def solution(A):
from math import sqrt
A_len = len(A)
next_peak = [-1] * A_len
peaks_count = 0
first_peak = -1
# Generate the information, where the next peak is.
for index in xrange(A_len-2, 0, -1):
if A[index] > A[index+1] and A[index] > A[index-1]:
next_peak[index] = index
peaks_count += 1
first_peak = index
else:
next_peak[index] = next_peak[index+1]
if peaks_count < 2:
# There is no peak or only one.
return peaks_count
max_flags = 1
max_min_distance = int(sqrt(A_len))
for min_distance in xrange(max_min_distance + 1, 1, -1):
# Try for every possible distance.
flags_used = 1
flags_have = min_distance-1 # Use one flag at the first peak
pos = first_peak
while flags_have > 0:
if pos + min_distance >= A_len-1:
# Reach or beyond the end of the array
break
pos = next_peak[pos+min_distance]
if pos == -1:
# No peak available afterward
break
flags_used += 1
flags_have -= 1
max_flags = max(max_flags, flags_used)
return max_flags