The BK-Tree – A Data Structure for Spell Checking | NullWords Blog
To build a BK-Tree all you have to do is take any word from your set and plop it in as your root node, and then add words to the tree based on their distance to the root.
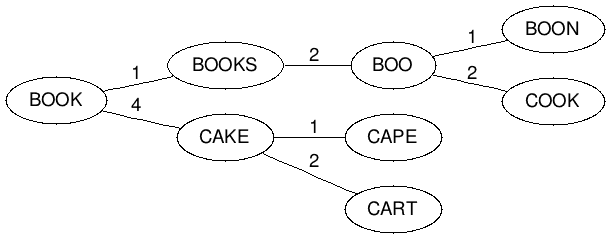Now that we have our structure the obvious question is how do we search it? This is simple as now all we need to do is take our misspelled word and find matches within a certain level of tolerance, which we’ll call N. We do this by taking the Levenshtein Distance of our word and compare it to the root, then crawl all nodes that are that distance ±N.
From this example it appears we can now find misspellings at a O(log n) time, which is better than our O(n) from before. This however doesn’t tell the whole story, because our tolerance can drastically increase the number of nodes we need to visit in order to do the search. Adiscussion over a BK-Tree implementation in Lucene seems to indicate a tolerance of 2 should limit a dictionary search to 5-10% of a tree
Java Implementation:
To build a BK-Tree all you have to do is take any word from your set and plop it in as your root node, and then add words to the tree based on their distance to the root.
Of course now if we add the word boo to the mix we get a conflict because:
LevenshteinDistance(book, boo) -> 1
which collides with books. To handle this we now have to chain boo from books by making it a child of books based on their Levenshtein Distance.
LevenshteinDistance(books, boo) -> 2
From this example it appears we can now find misspellings at a O(log n) time, which is better than our O(n) from before. This however doesn’t tell the whole story, because our tolerance can drastically increase the number of nodes we need to visit in order to do the search. Adiscussion over a BK-Tree implementation in Lucene seems to indicate a tolerance of 2 should limit a dictionary search to 5-10% of a tree
Java Implementation:
| public class BKTree { |
| public static class BKNode { |
| final String name; |
| final Map<Integer, BKNode> children = new HashMap<Integer, BKNode>(); |
| public BKNode(String name) { |
| this.name = name; |
| } |
| protected BKNode childAtDistance(int pos) { |
| return children.get(pos); |
| } |
| private void addChild(int pos, BKNode child) { |
| children.put(pos, child); |
| } |
| public List<String> search(String node, int maxDistance) { |
| int distance = distance(this.name, node); |
| List<String> matches = new LinkedList<String>(); |
| if (distance <= maxDistance) |
| matches.add(this.name); |
| if (children.size() == 0) |
| return matches; |
| int i = max(1, distance - maxDistance); |
| for (; i <= distance + maxDistance; i++) { |
| BKNode child = children.get(i); |
| if (child == null) |
| continue; |
| matches.addAll(child.search(node, maxDistance)); |
| } |
| return matches; |
| } |
| } |
| private BKNode root; |
| public List<String> search(String q, int maxDist) { |
| return root.search(q, maxDist); |
| } |
| /** |
| * Exact word search, same as {@link search(String, 1)} |
| * @param q |
| * @return match or empty string. |
| */ |
| public String search(String q) { |
| List<String> list = root.search(q, 1); |
| return list.isEmpty() ? "" : list.iterator().next(); |
| } |
| public void add(String node) { |
| if(node == null || node.isEmpty()) throw new IllegalArgumentException("word can't be null or empty."); |
| BKNode newNode = new BKNode(node); |
| if (root == null) { |
| root = newNode; |
| } |
| addInternal(root, newNode); |
| } |
| private void addInternal(BKNode src, BKNode newNode) { |
| if (src.equals(newNode)) |
| return; |
| int distance = distance(src.name, newNode.name); |
| BKNode bkNode = src.childAtDistance(distance); |
| if (bkNode == null) { |
| src.addChild(distance, newNode); |
| } else |
| addInternal(bkNode, newNode); |
| } |
| /** |
| * Computes Levenshtein distance of two strings. |
| * Adapted from http://en.wikipedia.org/wiki/Levenshtein_distance#Computing_Levenshtein_distance |
| * @param src |
| * @param tgt |
| * @return |
| */ |
| public static int distance(String src, String tgt) { |
| int d[][]; |
| if (src.length() == 0) { |
| return tgt.length(); |
| } |
| if (tgt.length() == 0) { |
| return src.length(); |
| } |
| d = new int[src.length() + 1][tgt.length() + 1]; |
| for (int i = 0; i <= src.length(); i++) { |
| d[i][0] = i; |
| } |
| for (int j = 0; j <= tgt.length(); j++) { |
| d[0][j] = j; |
| } |
| for (int i = 1; i <= src.length(); i++) { |
| char sch = src.charAt(i - 1); |
| for (int j = 1; j <= tgt.length(); j++) { |
| char tch = tgt.charAt(j - 1); |
| int cost = sch == tch ? 0 : 1; |
| d[i][j] = minimum(d[i - 1][j] + 1, //deletion |
| d[i][j - 1] + 1, //insertion |
| d[i - 1][j - 1] + cost); //substitution |
| } |
| } |
| return d[src.length()][tgt.length()]; |
| } |
| private static int minimum(int a, int b, int c) { |
| return min(min(a, b), c); |
| } |
| } |
Google Code: fuzzy-search-toolshttp://ntz-develop.blogspot.com/2011/03/fuzzy-string-search.html
http://blog.notdot.net/2007/4/Damn-Cool-Algorithms-Part-1-BK-Trees
To build the tree from a dictionary, take an arbitrary word and make it the root of your tree. Whenever you want to insert a word, take the Levenshtein distance between your word and the root of the tree, and find the edge with number d(newword,root). Recurse, comparing your query with the child node on that edge, and so on, until there is no child node, at which point you create a new child node and store your new word there. For example, to insert "boon" into the example tree above, we would examine the root, find that d("book", "boon") = 1, and so examine the child on the edge numbered 1, which is the word "rook". We would then calculate the distance d("rook", "boon"), which is 2, and so insert the new word under "rook", with an edge numbered 2.
To query the tree, take the Levenshtein distance from your term to the root, and recursively query every child node numbered between d-n and d+n (inclusive). If the node you are examining is within d of your search term, return it and continue your query.
The tree is N-ary and irregular (but generally well-balanced). Tests show that searching with a distance of 1 queries no more than 5-8% of the tree, and searching with two errors queries no more than 17-25% of the tree - a substantial improvement over checking every node!
Read full article from The BK-Tree – A Data Structure for Spell Checking | NullWords Blog
http://blog.notdot.net/2007/4/Damn-Cool-Algorithms-Part-1-BK-Trees
To build the tree from a dictionary, take an arbitrary word and make it the root of your tree. Whenever you want to insert a word, take the Levenshtein distance between your word and the root of the tree, and find the edge with number d(newword,root). Recurse, comparing your query with the child node on that edge, and so on, until there is no child node, at which point you create a new child node and store your new word there. For example, to insert "boon" into the example tree above, we would examine the root, find that d("book", "boon") = 1, and so examine the child on the edge numbered 1, which is the word "rook". We would then calculate the distance d("rook", "boon"), which is 2, and so insert the new word under "rook", with an edge numbered 2.
To query the tree, take the Levenshtein distance from your term to the root, and recursively query every child node numbered between d-n and d+n (inclusive). If the node you are examining is within d of your search term, return it and continue your query.
The tree is N-ary and irregular (but generally well-balanced). Tests show that searching with a distance of 1 queries no more than 5-8% of the tree, and searching with two errors queries no more than 17-25% of the tree - a substantial improvement over checking every node!
Read full article from The BK-Tree – A Data Structure for Spell Checking | NullWords Blog
