LeetCode - 308 Range Sum Query 2D - Mutable
leetcode Range Sum Query 2D - Immutable - 细语呢喃

The above rectangle (with the red border) is defined by (row1, col1) = (2, 1) and (row2, col2) = (4, 3), which contains sum = 8.
https://leetcode.com/problems/range-sum-query-2d-immutable/solution/
Approach #4 (Caching Smarter) [Accepted]
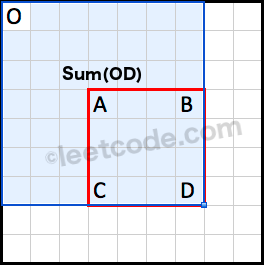
Sum(OD) is the cumulative region sum with respect to the origin at (0, 0).
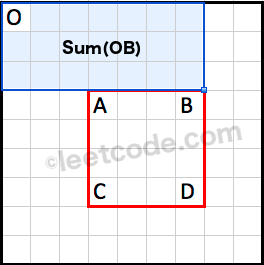
Sum(OB) is the cumulative region sum on top of the rectangle.
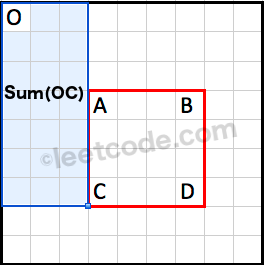
Sum(OC) is the cumulative region sum to the left of the rectangle.
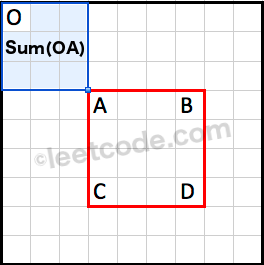
Sum(OA) is the cumulative region sum to the top left corner of the rectangle.
Approach #3 (Caching Rows) [Accepted]
Approach #2 (Caching) [Memory Limit Exceeded]
https://leetcode.com/discuss/69048/java-o-m-n-init-o-1-query-solution
private int[][] sums; public NumMatrix(int[][] matrix) { int m = matrix.length; if (m == 0) return; int n = matrix[0].length; sums = new int[m + 1][n + 1]; for (int i = 0; i < m; ++i) { int sumRow = 0; for (int j = 0; j < n; ++j) { sumRow += matrix[i][j]; sums[i + 1][j + 1] = sums[i][j + 1] + sumRow; } } } public int sumRegion(int row1, int col1, int row2, int col2) { return sums[row2 + 1][col2 + 1] - sums[row1][col2 + 1] - sums[row2 + 1][col1] + sums[row1][col1]; }
http://likemyblogger.blogspot.com/2015/11/leetcode-304-range-sum-query-2d.html
https://www.zybuluo.com/Yano/note/320394
要求是组数很⼤大不不能放⼊入内存。然后给的函数输⼊入很奇怪 是以矩形最左
下⻆角元素作为坐标原点设定⼀一个坐标轴,矩形位于第⼆二象限,然后给的是
两个点坐标,分别代表矩形左下⻆角那个点和右上⻆角那个点。
10月29 full time fb面经
屋溜零 一开始array都是正数,follow up是有负数 因为一开始就是按照有负数写的,所以直接过了
叁零寺 要求是组数很大不能放入内存 然后给的函数输入很奇怪 是以矩形最左下角元素作为坐标原点设定一个坐标轴,矩形位于第二象限,. From 1point 3acres bbs
然后给的是两个点坐标,分别代表矩形左下角那个点和右上角那个点。
leetcode Range Sum Query 2D - Immutable - 细语呢喃
Given a 2D matrix matrix, find the sum of the elements inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).

The above rectangle (with the red border) is defined by (row1, col1) = (2, 1) and (row2, col2) = (4, 3), which contains sum = 8.
Example:
Given matrix = [ [3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5] ] sumRegion(2, 1, 4, 3) -> 8 sumRegion(1, 1, 2, 2) -> 11 sumRegion(1, 2, 2, 4) -> 12
Note:
- You may assume that the matrix does not change.
- There are many calls to sumRegion function.
- You may assume that row1 ≤ row2 and col1 ≤ col2
https://leetcode.com/problems/range-sum-query-2d-immutable/solution/
Approach #4 (Caching Smarter) [Accepted]
We used a cumulative sum array in the 1D version. We notice that the cumulative sum is computed with respect to the origin at index 0. Extending this analogy to the 2D case, we could pre-compute a cumulative region sum with respect to the origin at .
- Time complexity : time per query, time pre-computation. The pre-computation in the constructor takes time. Each sumRegion query takes time.
- Space complexity : . The algorithm uses space to store the cumulative region sum.

Sum(OD) is the cumulative region sum with respect to the origin at (0, 0).
How do we derive using the pre-computed cumulative region sum?

Sum(OB) is the cumulative region sum on top of the rectangle.

Sum(OC) is the cumulative region sum to the left of the rectangle.

Sum(OA) is the cumulative region sum to the top left corner of the rectangle.
Note that the region is covered twice by both and . We could use the principle of inclusion-exclusion to calculate as following:
- Time complexity : time per query, time pre-computation. The pre-computation in the constructor takes time. Each sumRegion query takes time.
- Space complexity : . The algorithm uses space to store the cumulative region sum
Extra row and colum
private int[][] dp;
public NumMatrix(int[][] matrix) {
if (matrix.length == 0 || matrix[0].length == 0) return;
dp = new int[matrix.length + 1][matrix[0].length + 1];
for (int r = 0; r < matrix.length; r++) {
for (int c = 0; c < matrix[0].length; c++) {
dp[r + 1][c + 1] = dp[r + 1][c] + dp[r][c + 1] + matrix[r][c] - dp[r][c];
}
}
}
public int sumRegion(int row1, int col1, int row2, int col2) {
return dp[row2 + 1][col2 + 1] - dp[row1][col2 + 1] - dp[row2 + 1][col1] + dp[row1][col1];
}
Remember from the 1D version where we used a cumulative sum array? Could we apply that directly to solve this 2D version?
Algorithm
Try to see the 2D matrix as rows of 1D arrays. To find the region sum, we just accumulate the sum in the region row by row.
- Time complexity : time per query, time pre-computation. The pre-computation in the constructor takes time. The sumRegion query takes time.
- Space complexity : . The algorithm uses space to store the cumulative sum of all rows.
private int[][] dp;
public NumMatrix(int[][] matrix) {
if (matrix.length == 0 || matrix[0].length == 0) return;
dp = new int[matrix.length][matrix[0].length + 1];
for (int r = 0; r < matrix.length; r++) {
for (int c = 0; c < matrix[0].length; c++) {
dp[r][c + 1] = dp[r][c] + matrix[r][c];
}
}
}
public int sumRegion(int row1, int col1, int row2, int col2) {
int sum = 0;
for (int row = row1; row <= row2; row++) {
sum += dp[row][col2 + 1] - dp[row][col1];
}
return sum;
}
Approach #2 (Caching) [Memory Limit Exceeded]
Since sumRegion could be called many times, we definitely need to do some pre-processing.
Algorithm
We could trade in extra space for speed by pre-calculating all possible rectangular region sum and store them in a hash table. Each sumRegion query now takes only constant time complexity.
Complexity analysis
- Time complexity : time per query, time pre-computation. Each sumRegion query takes time as the hash table lookup's time complexity is constant. The pre-computation will take time as there are a total of possibilities need to be cached.
- Space complexity : . Since there are different possibilities for both top left and bottom right points of the rectangular region, the extra space required is .
https://leetcode.com/discuss/69048/java-o-m-n-init-o-1-query-solution
private int[][] sums; public NumMatrix(int[][] matrix) { int m = matrix.length; if (m == 0) return; int n = matrix[0].length; sums = new int[m + 1][n + 1]; for (int i = 0; i < m; ++i) { int sumRow = 0; for (int j = 0; j < n; ++j) { sumRow += matrix[i][j]; sums[i + 1][j + 1] = sums[i][j + 1] + sumRow; } } } public int sumRegion(int row1, int col1, int row2, int col2) { return sums[row2 + 1][col2 + 1] - sums[row1][col2 + 1] - sums[row2 + 1][col1] + sums[row1][col1]; }
http://likemyblogger.blogspot.com/2015/11/leetcode-304-range-sum-query-2d.html
vector<vector<int>> mt;public: NumMatrix(vector<vector<int>> &matrix) { int m = matrix.size(); if(m==0) return; int n = matrix[0].size(); if(n==0) return; mt.resize(m+1, vector<int>(n+1, 0)); for(int i=1; i<=m; ++i){ for(int j=1; j<=n; ++j){ mt[i][j] += matrix[i-1][j-1] + mt[i-1][j] + mt[i][j-1] - mt[i-1][j-1]; } } } int sumRegion(int row1, int col1, int row2, int col2) { return mt[row2+1][col2+1] - mt[row2+1][col1] - mt[row1][col2+1] + mt[row1][col1]; }https://www.zybuluo.com/Yano/note/320394
public long[][] sumMatrix;public NumMatrix(int[][] matrix) {if (matrix == null || matrix.length == 0) {return;}sumMatrix = new long[matrix.length + 1][matrix[0].length + 1];for (int i = 0; i < matrix.length; i++) {for (int j = 0; j < matrix[0].length; j++) {sumMatrix[i][j + 1] = sumMatrix[i][j] + matrix[i][j];}}}public int sumRegion(int row1, int col1, int row2, int col2) {if (sumMatrix == null || row1 < 0 || row2 < 0 || col1 < 0|| col2 < 0 || row1 >= sumMatrix.length - 1|| row2 >= sumMatrix.length - 1|| col1 >= sumMatrix[0].length - 1|| col2 >= sumMatrix[0].length - 1 || row1 > row2|| col1 > col2) {return Integer.MIN_VALUE;}long rt = 0;for (int i = row1; i <= row2; i++) {rt += sumMatrix[i][col2 + 1] - sumMatrix[i][col1];}return (int) rt;}
public class NumMatrix { int [][] sum; public NumMatrix(int[][] matrix) { if(matrix==null || matrix.length==0||matrix[0].length==0) return; int m = matrix.length; int n = matrix[0].length; sum = new int[m][n]; for(int i=0; i<m; i++){ int sumRow=0; for(int j=0; j<n; j++){ if(i==0){ sumRow += matrix[i][j]; sum[i][j]=sumRow; }else{ sumRow += matrix[i][j]; sum[i][j]=sumRow+sum[i-1][j]; } } } } public int sumRegion(int row1, int col1, int row2, int col2) { if(this.sum==null) return 0; int topRightX = row1; int topRightY = col2; int bottomLeftX=row2; int bottomLeftY= col1; int result=0; if(row1==0 && col1==0){ result = sum[row2][col2]; }else if(row1==0){ result = sum[row2][col2] -sum[bottomLeftX][bottomLeftY-1]; }else if(col1==0){ result = sum[row2][col2] -sum[topRightX-1][topRightY]; }else{ result = sum[row2][col2] -sum[topRightX-1][topRightY] -sum[bottomLeftX][bottomLeftY-1] +sum[row1-1][col1-1]; } return result; }https://github.com/mintycc/OnlineJudge-Solutions/blob/master/Leetcode/304_Range_Sum_Query_2D_Immutable.java
要求是组数很⼤大不不能放⼊入内存。然后给的函数输⼊入很奇怪 是以矩形最左
下⻆角元素作为坐标原点设定⼀一个坐标轴,矩形位于第⼆二象限,然后给的是
两个点坐标,分别代表矩形左下⻆角那个点和右上⻆角那个点。
10月29 full time fb面经
屋溜零 一开始array都是正数,follow up是有负数 因为一开始就是按照有负数写的,所以直接过了
叁零寺 要求是组数很大不能放入内存 然后给的函数输入很奇怪 是以矩形最左下角元素作为坐标原点设定一个坐标轴,矩形位于第二象限,. From 1point 3acres bbs
然后给的是两个点坐标,分别代表矩形左下角那个点和右上角那个点。